Компакти і їх властивості

Розділ 5. Компактні множини

Нехай Х – метричний простір, К – множина з цього простору.

Означення1.1. Множина К метричного простору Х, називається компактом, якщо з будь-якої послідовності елементів цієї множини можна виділити підпослідовність, збіжну до точки, яка належить К.

Теорема 1.1. Всякий компакт К метричного простору Х є замненою множиною.

Доведення. Нехай К компакт і х₀ гранична точка К. Візьмемо послідовність { x_n }, x_n є К, таку, що 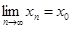(існування такої послідовності слідує з теореми 1.1. розділу 3.). Оскільки К компакт, то з { x_n } можна виділити підпослідовність 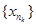, яка збігається до точки х^*, яка належить К. Оскільки границя послідовності і границя будь-якої її підпослідовності рівні, то х^*=х₀. Таким чином х₀ÎК, а це означає, що К є замкненою множиною.

Теорема 1.2. Всякий компакт К, метричного простору К є обмеженою множиною.

Доведення. Припустимо, що К необмежена множина. Виберемо довільну точку 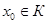. Тоді для кожного натурального числа п, знайдеться елемент х_п є К такий, що 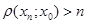. Візьмемо послідовність { x_n }. Так, як К є компактом, то з { x_n } можна виділити підпослідовність 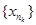, збіжну до точки х^*, яка належить К, 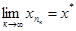. Це означає, що 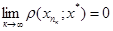. З нерівності 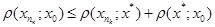слідує 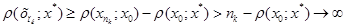, коли 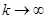. Прийшли до протиріччя. Теорему доведено.

Означення 1.2. Діаметром множини Е метричного простору Х, називається точна верхня межа множини { 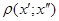}, де x^’, x^” є Е.

Теорема 1.3. Нехай задана послідовність 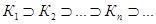компактів метричного простору Х. Тоді переріз 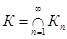не порожний.

Доведення. Вибравши в кожному К_п по точці х_п, одержимо послідовність . Так як К₁ є компакт, то з 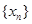можна виділити підпослідовність 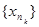,яка збігається до точки, яка належить К₁. Нехай 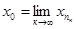. Оскільки при кожному п, починаючи з п_к>n, всі члени послідовності 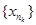належать К_п і К_п замкнена, то х₀ є К_п. А це значить, що .

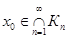Теорема 1.4. Нехай маємо послідовність 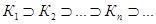компактів метричного простору Х, діаметри яких прямують до нуля. Тоді існує єдина точка, яка належить всім компактам.

Доведення. Те, що існує точка, яка належить всім компактам слідує з попередньої теореми. Покажемо, що така точка – єдина.

Припустимо, що існує хоча б дві різні точки х^’ i x^”, які належать всім компактам. Нехай 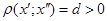, тоді діаметри всіх К_п не менші d. Так як діаметри компактів пямують до нуля, то починаючи з деякого номера, їхні діаметри будуть менші d. Прийшли до протиріччя. Теорему доведено.

§ 2. Компакти в просторі Rⁿ

Дата добавления: 2015-05-24