Критерій компактності

Відомо, що з будь-якої обмеженої послідовності {xn} дійсних чисел, можна виділити збіжну підпослідовність. Ця теорема називається теоремою Больцано-Вейєрштраса. Аналогічна теорема справедлива для послідовності з простору Rn.

Теорема 2.1. (теорема Больцано-Вейєрштраса в Rⁿ). З будь-якої обмеженої послідовності в просторі Rⁿ, можна виділити збіжну підпослідовність.

Доведення. Нехай маємо послідовність х⁽¹⁾, х⁽²⁾,…,х^(m),.. елементів простору Rⁿ, x^(m)=(x₁^(m), x₂^(m),…,x_n^(m)). Припустимо, що дана послідовність обмежена. Тоді існує точка х⁽⁰⁾=(х₁⁽⁰⁾. х₂⁽⁰⁾,…,х_п⁽⁰⁾) і дійсне число r таке, що 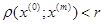, для всіх т. Тобто для всіх т виконується нерівність:

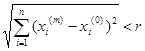(2.1).

З нерівності 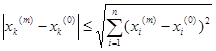, вірній при k=1,2,…,n, слідує, що кожна з числових послідовностей { x_k^(m) } – обмежена.

Візьмемо послідовність { x ₁ ^(m) }. На основі теореми Больцано-Вейєштраса для дійсних чисел, з цієї послідовності можна виділити збіжну підпослідовність , .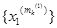

Розглянемо підпослідовність послідовності { x ₂ ^(m) }. З неї можна виділити збіжну підпослідовність 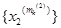. Нехай 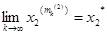, і т. д. З підпослідовності виділити збіжну підпослідовність , .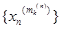

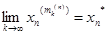Візьмемо підпослідовність 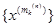, послідовності { х^(т) }, . Оскільки 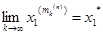, ,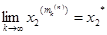..., , 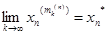то 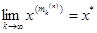, де х^*=(х ₁ ^*,...,х_п^*). Теорему доведено.

Іноді дану теорему формулюють в іншому вигляді.

Теорема 2.1^/. Будь-яка нескінченна обмежена множина в Rⁿ, має хоча б одну граничну точку.

Доведення. Нехай 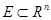обмежена нескінченна множина, тоді з неї можна виділити послідовність { х^(т) }, причому х^(k)¹ х^(р), якщо k¹p. Внаслідок теореми 2.1, з цієї послідовності можна виділити збіжну підпослідовність. Нехай границя цієї підпослідовності дорівнює х^*. На основі теореми 1.1 розділу 3 (критерію того, що дана точка є граничною точкою множини), х^* є Е^/.

Теорема 2.2. Для того, щоб множина К простору Rⁿ, була компактом, необхідно і достатньо, щоб вона була замкненою і обмеженою.

Доведення. Необхідність, слідує з теорем 2.1 і 2.2. Доведемо достатність.

Візьмемо послідовність { x^(m) }, х_т є К. З обмеженості множини К, слідує обмеженіть { x^(m) }. На основі теореми Больцано-Вейєрштраса, з цієї послідовності можна виділити збіжну підпослідовність 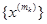. Нехай 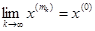. Очевидно х⁽⁰⁾ – точка дотику множини К. З замкненості К випливає, що х⁽⁰⁾ є К. Звідси робимо висновок, що К – компакт.

Нехай маємо множину Е метричного простору Х і { Y_a } – система відкритих множин цього простору.

Означення 3.1. Говорять, що система { Y _a} відкритих множин, покриває множину Е, якщо кожна точка х є Е, належить хоча б одній з множин Y_a, цієї системи.

Теорема 3.1. (Гейне-Бареля). Нехай К – компакт, який належить метричному простору Х. Тоді з будь-якого відкритого покриття 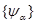компакта К можна виділити скінченне підпокриття.

Доведення. Нехай К – компакт, 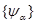– довільне відкрите покриття К. Спочатку доведемо, що існує e₀>0 таке, що при будь-якому х є К, куля S(x, e₀ ) входить цілком в деяку множину .

Припустимо, що це не так. Тоді знайдеться послідовність чисел e _п®0, e _п>0 і точок х_п є М, таких, що кулі S(x_n, e _п) не ввійдуть ні в одну з множин Y_a. З послідовності { x_n }, можна виділити підпослідовність 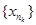, яка збігається до точки х₀ є К (внаслідок того, що К компакт). Так, як система 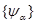покриває К, то знайдеться множина 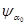з цієї системи така, що . Внаслідок того, що 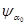є відкритою множиною, то 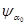цілком містить деяку кулю 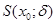. Виберемо п_к настільки великим, щоб 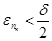і 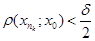, з нерівності 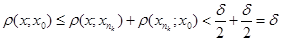, справедливої для будь-якого х із кулі 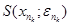, робимо висновок, що 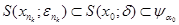, хоча за побудовою 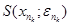не може входити ні в одне . Це протиріччя доводить справедливість твердження.

Нехай e₀>0 вибране так, що виконується вище доведене твердження. Покажемо, що існує скінченна кількість точок 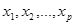, , що .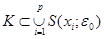

Припустимо, що це не так. Візьмемо довільне х ₁Î К. Тоді існує х ₂Î К таке, що r(х ₁; x ₂)³e₀ (в іншому випадку компакт містився б у кулі S (x ₁;e₀)). Аналогічно існує х ₃Î К, таке, що r(х ₁; x ₃)³e₀, r(х ₂; x ₃)³e₀ і т.д. Одержимо послідовність { x_n }, таку, що r(х_i;x_j)³e₀, при i¹j. Очевидно, що жодна підпослідовність цієї послідовності не є фундаментальною, а значить і збіжною. Прийшли до протиріччя.

Таким чином існує скінченна кількість точок х ₁, х ₂,..., х_р, х_і Î К, що 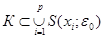. Так, як 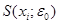цілком входить в деяку множину 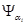, то 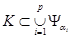. Теорему доведено.

Теорема 3.2. Нехай К – непорожня множина метричного простору Х. Якщо із будь-якої системи { Y _a}, відкритих множин, яка покриває К, можна виділити скінченне підпокриття, то К – компакт.

Доведення. Припустимо, що К не є компактом. Тоді існує послідовність { х_п } така, що з неї не можна виділити підпослідовніть, яка збігається до точки множини К. Тоді кожна точка х множини К має окіл S(x;e) (e­ - залежить від х) в якому міститься не більше, як скінченна кількість елементів послідовності. (Якби в довільному околі якоїсь точки х^* є К, міститься нескінченна множина точок послідовності, то існувала б підпослідовність 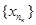послідовності { х_п }, яка б збігалася до до х^*). Множина куль S(x;e) покриває множину К. Внаслідок умови теореми, існує скінченна кількість куль S(у_і, e _і), (і=1,2,...,р), які покривають К. Так, як всі елементи послідовності { х_п } містяться в 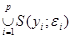, а в кожній S(у_і, e _і) міститься скінченна кількість елементів послідовності, то { х_п } має скінченну кількість елементів, що суперечить означенню послідовності. Теорему доведено.

З теорем 3.1 і 3.1, слідує критерій того, що К є ком пактом.

Теорема 3.3. Для того, щоб множина К метричного простору Х була компактом, необхідно і достатньо, щоб з кожного відкритого покриття К можна було виділити скінченне підпокриття.

Дата добавления: 2015-05-24