Теорема Банаха

(2.2).

(2.1).

Із (2.1) випливає, що для 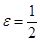знайдеться n ₁ ÎN: "m>n ₁,

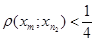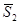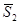Утворимо замкнену кулю з центром в і радіусом рівним 1. На основі нерівності (2.1), для , знайдеться n₂Î N, n₂>n₁: "m>n₂Þ . Утворимо знову замкнену кулю з центром в і радіусом рівним 1/2. Зазначимо, що . Візьмемо будь-яке xÎ , тоді

,

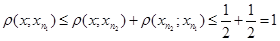звідси випливає, що . Отже . Продовжуючи цей процес, одержимо послідовність вкладених замкнених куль 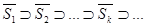радіуси яких прямують до нуля, а центри знаходяться в точках 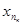. На основі припущення теореми, існує точка х₀, яка належить всім 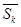. Оскільки для кожного k виконується нерівність , то 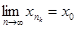. Так, як фундаментальна послідовність { x_n } має збіжну підпослідовність , то на основі теореми 1.6. розділу 2, послідовність { x_n } збіжна. Теорему доведено.

Теорема 2.3. Нехай в повному метричному просторі маємо послідовність вкладених одна в одну замкнених куль, радіуси яких прямують до нуля. Тоді існує єдина точка, яка належить всім цим кулям.

Доведення. Нехай – послідовність замкнених куль, які задовільняють умові теореми: 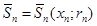, r_n®0, коли . Існування точки спільної всім кулям слідує з теореми 2.2. Припустимо, що таких точок є більше ніж одна і нехай 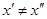– точки, які належать всім кулям. Так, як при всіх п, то маємо , що неможливо, бо r_n®0 при п®¥. Значить точка, яка є спільною для всіх куль – єдина.

Одним із важливих прикладів неперервних відображень є, так звані, стискуючі відображення.

Означення 3.1. Нехай f відображення метричногопростору X₁ в X₂. Відображення називається стискуючим, якщо $a: 0<a<1: " x, yÎX₁, справедлива нерівність: .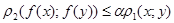

Легко показати, що стискуюче відображення є неперервним. Дійсно, нехай х₀ÎХ₁. Тоді 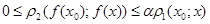. Якщо х®х₀, то , а значить 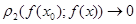. Отже, відображення є неперервним.

Дуже часто в математиці виникає потреба з’ясувати при яких умовах те чи інше рівняння має на деякій множині єдиний розв’язок. При розв’язуванні цієї задачі використовують властивості стискуючих відображень заданих в повних метричних просторах.

Означення 3.2. Нехай f відображає Х в Х. Точка х₀ÎХ, називається нерухомою точкою оператора f, якщо f(x₀)=x₀.

Теорема (Банаха). Якщо f:X®X є стискуючим відображенням, і Х повний метричний простір, то відображення f в даному просторі має єдину нерухому точку.

Доведення. Візьмемо довільне х₀ÎХ, х₁=f(x₀), x₂=f(x₁)_,…x_n=f(x_n-1),… В результаті одержали послідовність { x_n }Ì X. Тоді

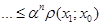(3.1).

Візьмемо будь-яке пÎN, тоді "pÎN

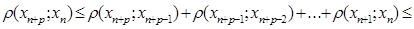(a ^n+p-1+a^n+p-2+…...+aⁿ) r (x₁;x₀)<(aⁿ+aⁿ⁺¹+…+a^n+p-1+a^n+p+…) r (x₁;x₀)= r (x₁;x₀).

Оскільки 0 <a< 1, то останній вираз при п®¥, прямує до нуля так, що " e > 0, $ n₀ÎN: " n³n₀, справедлива .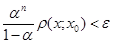

З останніх двох нерівностей одержуємо, що послідовність { x_n } є фундаментальною, а оскільки простір повний, то і збіжною до деякої точки аÎХ.

Внаслідок неперервності відображення f маємо:

Дата добавления: 2015-05-24