Достатні умови диференційовності функції багатьох змінних

.

Але дана функція не є неперервною в точці (0;0), тому вона не може бути і диференційовною в цій точці.

Таким чином цей приклад показує:

1)Із існування всіх часткових похідних в точці, не випливає диференційовність цієї функції в цій точці.

2)Не обов’язково розривна функція не повинна мати часткових похідних.

Зауважимо, що в означенні диференційовної функції на 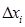накладається умова: .

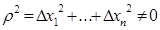З теореми 1.1. бачимо, що якщо функція диференційовна в точці х₀, то її приріст можемо записати у вигляді

, де a_і – нескінченно малі функції від .

Якщо – незалежні змінні, то їх прирости називаються диференціалами, тобто: .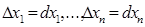

Таким чином диференціал функції можна записати у вигляді .

Як ми знаємо, між диференційовністю функції однієї змінної в якійсь точці х₀ і наявністю дотичної до графіка функції в точці (х₀, f(x₀)), є зв’язок. Перенести його на функцію будь-якої кількості змінних (³3) – не можливо, бо графік такої функції буде розміщуватись в просторі розмірності >3. Та все ж таки для функції z=f(x;y) таку проблему можна ставити, бо її графіком буде деяка поверхня в просторі R³, для якої ми можемо ввести поняття дотичної площини, а отже, можливо, і зможемо зв’язати проблему існування дотичної площини з умовою диференційовності функції.

Означення 2.4. Площина Р, називається дотичною до деякої поверхні G в деякій точці М₀(у₀; x₀; z₀) цієї поверхні, якщо:

1) М₀ÎР;

2) кут між цією площиною і січною М₀М, де М – будь-яка точка поверхні G, прямує до нуля, якщо точка М прямує до співпадання з точкою М₀.

Нехай функція z=f(x; y) диференційовна в точці А(х₀; y₀), тоді приріст функції можна записати у вигляді , _, коли r®0, де _.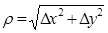

Розглянемо площину: і покажемо, що вона є дотичною до поверхні в точці (х₀; y₀; z₀), де z₀=f(x₀; y₀). Для того, щоб довести, що ця площина буде дотичною до нашої поверхні в точці (х₀; y₀; z₀) потрібно показати:

1) що вона проходить через точку (х₀; y₀; z₀), а це очевидно, бо координати цієї точки наше рівняння задовільняють;

2) що кут між нормаллю цієї площини і січною прямуватиме до 90°, коли точка М прямує до точки М₀, рухаючись по цій поверхні.

Нехай 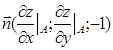– - вектор нормалі до площини в точці М₀. Розглянемо вектор 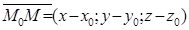, де М(х; y; z) – довільна точка на поверхні.

Врахувавши, що , одержимо:

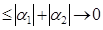, коли ,

це рівнозначне тому, що коли М®М₀ по поверхні, то кут між 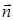і прямує до 90 °, а це означає, що кут між площиною і січною прямує до нуля.

Отже площина є дотичною до функції в точці М₀(х₀; y₀; z₀).

В попередньому параграфі ми показали, що, якщо функція диференційовна в точці, то в даній точці існують часткові похідні. Обернене твердження взагалі кажучи не вірне. Але при цьому має місце наступна теорема.

Теорема 2.1. Нехай функція U=(x ₁; x₂;…;x_n) в деякому околі точки А(х ₁ ⁽⁰⁾; x₂⁽⁰⁾;…;x_n⁽⁰⁾) має всі частинні похідні. Якщо вони є функціями неперервними в точці А, то дана функція – диференційовна в цій точці.

Доведення. Для простоти викладу будемо вважати, що наша функція залежить від двох змінних, U=f(x; y), A(x₀; y₀).

Надамо х₀, у₀ прирости такі, що точка 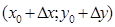належить околу, в якому існують часткові похідні. Використовуючи теорему Лагранжа, одержимо:

, де 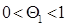, . Оскільки за умовою f ^/_x і f ^/_y – неперервна в точці х₀, у₀, то величини і 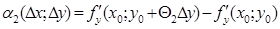прямують до нуля, коли . Знайшовши з останніх двох рівностей перші доданки справа і підставивши їх у суму, одержимо: 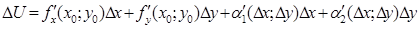, а це означає, що наша функція в точці А є диференційовною. Теорему доведено.

Дата добавления: 2015-05-24