
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Достатні умови незалежності змішаних частинних похідних від порядку диференціювання
|
|
|
|
В вище наведеному прикладі змішані похідні 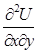 ;
; 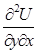 функції
функції 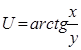 були рівні. Наступний приклад показує, що це не завжди так.
були рівні. Наступний приклад показує, що це не завжди так.
Нехай 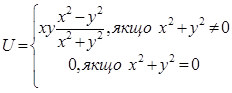 .
.
Тоді 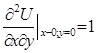 ;
; 
Розглянемо достатні умови незалежності змішаних частинних похідних від порядку диференціювання.
Означення 2.1. Функція U=f(x 1 ,…,xn), називається т раз диференційовною в точці М0(х 1 (0),...,хп(0)), якщо всі частинні похідні (т- 1 )- го порядку є функціями диференційовними в цій точці.
Теорема 2.1. Для того, щоб функція U=f(x 1 ,…,xn) була т раз диференційовною в точці М0(х 1 (0),...,хп(0)) достатньо, щоб її частинні похідні т- го порядку були визначені в деякому околі точки М0 і були неперервними функціями в цій точці.
Справедливість цього твердження слідує з теореми про достатню умову диференційовності функції.
Теорема 2.2. (про рівність змішаних похідних другого порядку). Якщо функція U=f(x,у) двічі диференційовна в точці М0(х0, у0), то  .
.
Доведення. Так як функція U=f(x;y) двічі диференційовна в точці М0, то частинні похідні f / x(x;y) і f /y(x;y) визначені в деякому околі точки М0.
Розглянемо вираз
F=f(x0+h, y0+h)-f(x0+h, y0)-f(x0, y0+h)+f(x0;y0), (2.1),
де h – довільне число, таке, що точка М0(х0+h, y0+h) міститься у вище вказаному околі. Переписавши F у вигляді
F=(f(x0+h, y0+h))-f(x0+h, y0))-(f(x0, y0+h)-f(x0;y0)),
помічаємо, що це F є приростом функції j(х)=f(x, y0+h)-f(x, y0) в точці х0. Тобто
F=Dj(х0)=j(х0+h)-j(х0) (2.2).
Оскільки функція j(х) на [ х0, х0+h ] задовільняє умові теореми Лагранжа, то
F=j¢(х0+q 1 ,h)h=(f¢x(x0+q 1 h,y0+h)-f¢x(x0+q 1 h,y0))h=(f¢x(x0+q 1 h,y0+h)-f¢x(x0,y0)-(f¢x(x0+q 1 h,y0)-f¢x(x0,y0)))h (2.3).
де 0 <q 1 < 1. Так, як f¢x(x,y) - диференційовна в точці М0, то
f¢x(x0+q 1 h,y0+h)-f¢x(x0,y0)=f¢¢xx(x0,y0) q 1 h+f¢¢xy(x0,y0)h+a 1 (h) q 1 h+a2(h)h, (2.4).
f¢x(x0+q 1 h,y0)-f¢x(x0,y0)=f¢¢xx(x0,y0) qh+a3(h) q 1 h, (2.5)
при цьому a 1 (h), a2(h),a3(h) прямують до нуля, коли h®0.
Підставивши (2.4) і (2.5) в (2.3), одержимо:
F=((f¢¢xx(x0,y0)q 1 h+f¢¢xy(x0,y0)h+a 1 (h)q 1 h+a2(h)h)-((f¢¢xx(x0,y0)q 1 h+a3(h) q 1 h))h=(f¢¢xy(x0,y0)+a 1 (h) q 1 +a2(h)-a3(h) q 1 )h2=(f¢¢xy(x0,y0)+g 1 (h))h2 , (2.6),
де g 1 (h)=a 1 (h)q 1 +a2(h)+a3(h)q 1.
Переписавши F у наступному вигляді
F=(f(x0+h,y0+h)-f(x0,y0+h))-(f(x0,y0+h)-f(x0,y0)),
бачимо, що F є приростом функції Y(y)=f(x0+h,y)-f(x0,y) в точці у0. Застосувавши теорему Лагранжа і врахувавши диференційовність f¢y(x,y) в точці М0, ми отримаємо наступне представлення для F,
F=(f¢¢yx(x0,y0)+g2(h))h2 (2.7),
при цьому a2(g)®0, коли h®0.
Прирівнявши праві частини рівностей (2.6) і (2.7) і скоротивши на h2, отримаємо:
f¢¢xy(x0,y0)+g 1 (h)=f¢¢yx(x0,y0)+g2(h) (2.8).
Перейшовши до границі, коли h®0, отримаємо: f¢¢xy(x0,y0)=f¢¢yx(x0,y0). Теорема доведена.
Наступна теорема теж дає достатні умови рівності змішаних похідних другого порядку.
Теорема 2.3. Нехай в деякому околі точки М0(х0,у0) функція U=f(x,y) має частинні похідні f¢x, f¢y, f¢¢xy, f¢¢yx. Якщо f¢¢xy і f¢¢yx неперервні в М0, то f¢¢xy(x0,y0)=f¢¢yx(x0,y0).
Доведення. Розглянемо F=f(x0+h, y0+h)-f(x0+h, y0)-f(x0, y0+h)+f(x0;y0). Замітимо, що F=Dj(х0), де j(х)=f(x, y0+h)-f(x, y0). Застосувавши теорему Лагранжа до j(х), отримаємо:
F=(f¢x(x0+q 1 h,y0+h)-f¢x(x0+q 1 h,y0)), де 0< q 1 < 1.
Застосувавши теорему Лагранжа до функції t(y)=f¢x(x0+q1h,y) на відрізку [ у0,у0+h ], одержимо
F=f¢¢xy(x0+q1h,y0+q2h)h2, 0<q2<1.
Внаслідок неперервності f¢¢xy(x,y) в точці (х0,у0), маємо
F=(f¢¢xy(x0,y0)+g 1 (h))h2 (2.9),
де g 1 (h)®0, коли h®0. Представивши F у вигляді F=Dy(у), де y(у)=f(x0+h,y)-
-f(x0,y), аналогічно одержуємо
F=(f¢¢yx(x0;y0)+g2(h))h2 (2.10),
де g2(h)®0, коли h®0. Прирівнявши праві частини рівностей (2.9) і (2.10), скоротивши на h2 і перейшовши до границі, коли h прямує до нуля, отримаємо f¢¢xy(x0;y0)=f¢¢yx(x0;y0).
Теорема 2.4. Якщо U=f(x0;…;xn) m разів диференційовна в точці М0, то змішана частинна похідна, в цій точці, не залежить від порядку повторного диференціювання.
Доведення. Очевидно, достатньо довести незалежність значень давільної т- тої змішаної похідної від порядку проведення двох послідовних диференціювань. Тобто достатньо довести рівність:
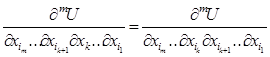 (2.11).
(2.11).
Розглянемо функцію 
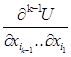 . Ця функція є диференційовною функцією від змінних
. Ця функція є диференційовною функцією від змінних 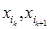 , тому внаслідок теореми 2.2. маємо:
, тому внаслідок теореми 2.2. маємо:
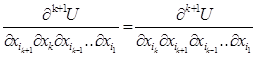 .
.
Звідси і слідує рівність (2.11). Теорему доведено.
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 1157; Нарушение авторских прав?; Мы поможем в написании вашей работы!