Похідна за напрямком. Градієнт

Інваріантність форми диференціала функції багатьох змінних.

Нехай функція U=f(x ₁ ,…,x_n) диференційовна в точці В, а функції х _{1 =} j ₁ (t ₁ ,…,t_k),…,x_n=j_n(t ₁ ,…, t_k), як вимагалось в теоремі 3.2 – диференційовні в точці А, при чому координати точки В зв’язані з координатами точки А, як і вимагалось в цій теоремі. Тоді, як ми довели, U(t ₁ …,t_k) диференційовна в точці А. А оскільки t_i – незалежні аргументи, то існує диференціал нашої функції дорівнює:

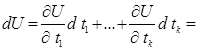
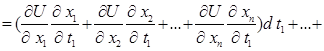
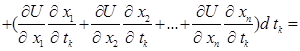
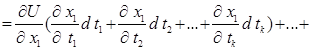
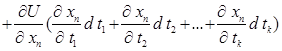
Так, як 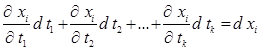при кожному і, то dU можна переписати у вигляті:

,

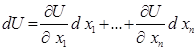а останній вираз не відрізняється від dU, коли х₁,...,х_n – незалежні змінні.

Отже ми довели: форма диференціала функції багатьох змінних не залежить від того, чи її аргументи – незалежні змінні, чи функції якихось інших знінних. Ця властивість називається інваріантністю форми диференціала.

Нехай маємо напрямок в точці М₀(х₀, у₀, z₀)ÎR³, заданий одиничним вектором 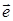, який утворює, з додатніми напрямками осей ОХ, ОУ, ОZ, кути, що відповідно дорівнюють a, b, g. Через точку М₀ проведемо пряму, яка проходить вздовж вектора 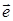. За додатній напрямок візьмемо напрям вектора 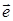. На цій прямій виберемо точку М, відмінну від М₀.

Означення 5.1. Орієнтовною довжиною відрізка М₀М з початком в точці М₀ і кінцем в точці М, називається число, яке дорівнює довжині цього відрізка, коли напрям вектора 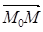співпадає з напрямом 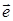, або число, яке дорівнює довжині цього відрізка взятій із знаком мінус, коли напрямки векторів 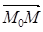і 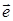– протилежні.

Нехай функція U=f(x, y, z) – визначена в деякому околі точки М₀(х₀,у₀,z₀), точка М, відмінна від М₀, яка лежить на вище згаданій прямій і належить даному околу.

Означення 5.2. Якщо існує границя 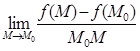, то її називають похідною функції f(x,y,z) в точці М₀ за напрямком вектора 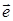і позначають: , .

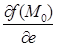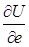Таким чином 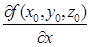, , 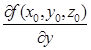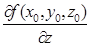є похідними за напрямками, які визначаються відповідно додатніми напрямками осей ОХ, ОУ, ОZ.

Теорема 5.1. Якщо функція f(x,y,z) диференційовна в точці М₀(x₀,y₀,z₀), то в цій точці вона має похідну за будь-яким напрямком 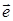і при цьому виконується рівність:

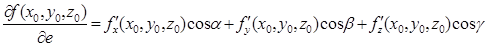. (5.1)

Доведення. Нахай маємо точку М₀ і через неї проведена пряма, яка проходить через вектор 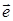. На прямій взято точку 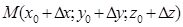, 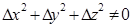. Так, як функція диференційовна в точці М₀, то

,

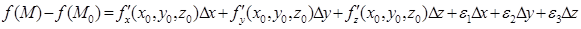де e ₁, e₂, e₃ прямують до нуля, коли Dх®0, Dу®0, Dz®0. Оскільки Dх=М₀Мcosa, Dу=М₀Мcosb, Dz=М₀Мcosg, то

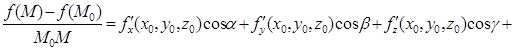
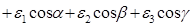. (5.2).

Оскільки, якщо М®М₀, то Dх, Dу, Dz,®0, а значить і e₁, e₂, e₃ прямують до нуля. Таким чином права частина рівності (5.2) (а отже і ліва), має границю, коли М®М₀, що дорівнює

.

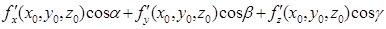Це означає, що похідна за напрямком 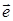існує і виконується рівність (5.1).

Теорему доведено.

Нехай функція U=f(x,y,z) диференційовна в точці М₀(х₀,у₀,z₀). Тоді за теоремою 5.1, в цій точці існує похідна функції за будь-яким напрямком. Часто виникає питання: за яким напрямком ця похідна буде найбільша?

Розглянемо два вектори: одиничний вектор 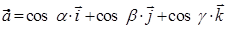, який визначає напрямок, і 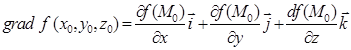, який називається градієнтом функції f(x,y,z) в точці М₀(x₀,y₀,z₀), тут 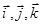– орти. Скалярний добуток ( 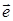, gradf(x₀,y₀,z₀)) цих векторів, дорівнює:

.

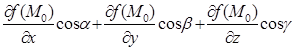Порівнявши з формулою (5.1) ми бачимо

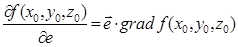(5.3).

З іншого боку

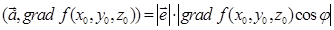(5.4),

де j – кут між цими векторами. Так, як 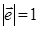, то з формул (5.3), (5.4), одержимо:

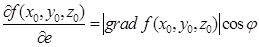(5.5).

Права частина (а значить і ліва), якщо f(x₀,y₀,z₀)¹0, набуває найбільшого значення при j=0. Таким чином, якщо 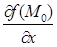, , 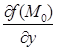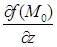одночасно не дорівнюють нулю, то найбільшого значення похідна за напрямком набуває в напрямі градієнта даної функції. Похідна в цьому напрямі дорівнює:

.

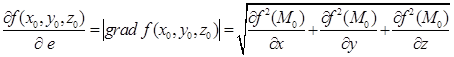Врахувавши, що 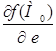дорівнює швидкості зміни функції в напрямі, який визначається вектором 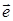, то можна сказати, що якщо градієнт функції в точці М₀ не дорівнює нулю, то він напрямлений в бік найбільшого зростання функції.

Дата добавления: 2015-05-24