Формула Тейлора для функцій багатьох змінних

Як відомо, для функції U=F(t) (п+ 1) раз диференційовної в околі точки t₀, має місце рівність:

,

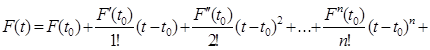
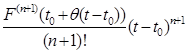де 0<q<1.

Запишемо дещо по-іншому цю формулу. Нехай t-t₀=Dt, тоді:

F(t)-F(t₀)=DF(t₀)

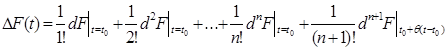(4.1)

Дивлячись на цей вигляд формули Тейлора, неважко догадатись, що її можна перенести і на функції багатьох змінних.

Теорема 4.1 (Формула Тейлора для функції багатьох змінних)

Нехай функція U=F(x ₁ ;x₂;…;x_k) (n+ 1 ) раз диференційовна в деякому околі точки М₀(х ₁ ⁽⁰⁾,....,х_к⁽⁰⁾), тоді справедлива рівність:

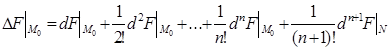, (4.1)

де 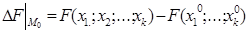і точка N(х₁,...,х_к) належить заданому околу. В диференціалах, які стоять справа, dx_i=Dx_i=x_i-x_i⁽⁰⁾, останній доданок цієї формули, називається залишковим членом формули Тейлора у формі Лагранжа.

Доведення. Для простоти викладу доведемо цю формулу для функції двох змінних.

Нехай функція U=F(x ₁ ;x₂), яка (п+ 1 ) разів диференційовна в околі точки М₀(х ₁ ⁽⁰⁾;x₂⁽⁰⁾).

Візьмемо точку М ₁ (х ₁ ⁽⁰⁾+Dх ₁ ;x₂⁽⁰⁾+Dx₂). Проведемо через точки М₀ і М ₁ пряму, рівняння якої буде: ;

Звідки ; .

При цьому, якщо tÎ [ 0;1 ], то М(х ₁ ;x₂) пробіжить відрізок М₀М ₁.

Розглядатимемо функцію U=F(x ₁ ;x₂) лише в точках відрізка М₀М ₁. На цьому відрізку ця функція є функцією однієї змінної t: U=F(x ₁ ⁽⁰⁾+tDx ₁ ;x ₂ ⁽⁰⁾+tDx ₂ )=f(t). З того, що х ₁, і х ₂ є лінійними функціями від t і задана функція (п+ 1) разів диференційовна в околі точки М ₀слідує, що ця складна функція по t є (п+ 1) раз диференційовною в околі точки t ₀=0. Тоді з формули (4.1), одержуємо:

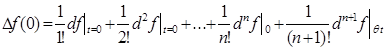(4.2).

Замітимо, що в нашому випадку

Df(0)=F(x ₁ ⁽⁰⁾+Dx ₁ ;x₂⁽⁰⁾+Dx₂)-F(x ₁ ⁽⁰⁾;x₂⁽⁰⁾)=f( 1 )-f(0)=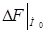

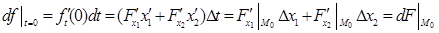
Оскільки, як ми встановили вище, диференціали вищих порядків мають властивість інваріантності форми, якщо змінні лінійно залежать від інших аргументів, (від t), то всі інші доданки формули (4.2) матимуть вигляд 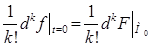; k= 1 ,2,…n

, де NÎ [ М₀;M ₁]. Врахувавши це все, і, підставивши у формулу (4.2), ми одержимо формулу Тейлора, де в точці N, буде деяка точка на [ М₀;М ₁]. Теорему доведено.

Дана формула Тейлора дозволить нам в наступних параграфах вирішувати проблеми екстремумів функцій багатьох змінних.

Дата добавления: 2015-05-24