Інформатика як наука 2 страница

Інформаційна ентропія — міра невизначеності або непередбачуваності інформації, невизначеність появи якого-небудь символу первинного алфавіту. За відсутності інформаційних втрат чисельно рівна кількості інформації на символ повідомлення, яке передається [2, 5]. Наприклад, в послідовності букв, що становлять яке-небудь речення на російській мові, різні букви з'являються з різною частотою, тому невизначеність появи для деяких букв менше. Якщо ж врахувати, що деякі поєднання букв (в цьому випадку говорять про ентропію n-ого порядку) зустрічаються рідко, то невизначеність ще більш зменшується.

Ентропія — це кількість інформації, що доводиться на одне елементарне повідомлення джерела, яке виробляє статистично незалежні повідомлення. За одиницю кількості інформації прийнята така кількість інформації, яка містить повідомлення, що зменшує невизначеність знання в два рази. Така одиниця названа біт (від binary digit - двійкова цифра).

Ентропія є кількістю, визначеною в контексті моделі ймовірності для джерела даних. Наприклад, кидок монети має ентропію, рівну 1 біт на один кидок (за умови його незалежності). У джерела, яке генерує рядок, що складається тільки з букв «А», ентропія рівна нулю. Так, наприклад, дослідним шляхом можна встановити, що ентропія англійського тексту рівна 1,5 біт на символ, що, звичайно, варіюватиметься для різних текстів. Ступінь ентропії джерела даних означає середнє число бітів на елемент даних, що вимагаються для її зашифровування без втрати інформації, при оптимальному кодуванні.

Деякі біти даних можуть не нести інформації. Наприклад, структури даних часто зберігають надмірну інформацію, або мають ідентичні секції незалежно від інформації в структурі даних. Кількість ентропії не завжди виражається цілим числом біт.

Ентропія обмежує максимально можливе стиснення без втрат (або майже без втрат), яке може бути реалізоване при використанні теоретично - типового набору або, на практиці, - кодування Хаффмана, кодування Лемпеля - Зіва - Велча або арифметичного кодування [12].

Інформація, також як і фізичні величини, має розмірність і одиниці вимірювання (для носіїв комп'ютера). Якнайменша одиниця представлення інформації – це двійковий розряд, або бит (bit - binary digit). У біта всього два можливі значення: Ні/Так, 0/1. Засоби обчислювальної техніки обробляють інформацію у вигляді байтів. Байт – це група з 8 бит. Одним байтом можна виразити 256 різних значень (від 0 до 255).

Похідні одиниці вимірювання інформації:

- приставка кіло в інформатиці означає не тисячу, а 2¹⁰, тобто 1024;

- мега - 2²⁰, тобто 1048576 (більше мільйона);

- гига - 2³⁰, тобто 1073741824 (більше мільярда);

- 1 кілобайтів (Кб) = 1024 байти;

- 1 мегабайт (Мб) = 1024 Кб =1048576 байта;

- 1 Гігабайт (Гб) = 1024 Мб = 1048576 Кб = 1073741824 байти.

1.2.2. Кодування чисел і арифметичні дії в різних системах числення

Пристрої обчислювальної техніки працюють з цифровою інформацією. Переведення інформації з аналогової форми в цифрову називається оцифровкою. Цифрова інформація зберігається у вигляді числового двійкового коду. Всі числа в комп'ютері представлені за допомогою нулів і одиниць.

З технічної сторони, двійкова система числення ефективно реалізує основні функції комп'ютера. Введення чисел в комп'ютер і виведення їх для сприйняття людиною виконується, звичайно, в десятковій системі числення. Перетворення з десяткової системи в двійкову і навпаки автоматично виконують програми. Це перетворення нескладне і доступно для розуміння.

В спеціальній літературі для опису оброблюваних комп'ютером даних, змісту оперативної пам'яті і т.п. часто використовується шістнадцяткова система числення. Вона зручна тим, що дуже просто співвідноситься з двійковою системою: одна шістнадцятирічна цифра відповідає чотирьом двійковим розрядам (для шістнадцяткових цифр, які більше дев'яти, використовують позначення А – десять, В – одинадцять, З – дванадцять, D – тринадцять, Е – чотирнадцять, F – п'ятнадцять). Проміжної між двійковою і шістнадцятковою системами є вісімкова, в якій одна вісімкова цифра відповідає трьом двійковим розрядам.

Приклад відповідного представлення чисел в двійковій, вісімковій і шістнадцятковій системах числення наведений в таблиці 1.2.

Таблиця 1.2 - Представлення чисел в різних системах числення

Десяткова	Двійкова	Вісімкова	Шістнадцяткова
Розряди
десятки	одиниці
										A
										B
										C
										D
										E
										F

Проаналізуємо число 1997, записане в десятковій системі числення (с\ч):

Тисячі	Сотні	Десятки	Одиниці

1997 = 1 * 10³ + 9 * 10² + 9 * 10¹ + 7 * 10⁰

Очевидно, що в десятковому числі кожний наступний розряд більше попереднього в 10 разів. Тобто число 10 – це параметр с\ч, званий основа і для десяткової системи він дорівнює 10 (Q = 10).

Крім того, видно, що в даному випадку в кожному розряді можуть використовуватися цифри від 0 до 9, тобто теж 10 штук. Ці числа теж параметри системи (А = 0, 1, 2., 9).

В двійковій с\ч ці параметри рівні: Q = 2; А = 0, 1.

При переведенні чисел із десяткової системи числення в систему з основою Q > 1 звичайно використовують наступний алгоритм:

1) ціла частина переводиться шляхом поетапного ділення на Q. В трьох колонках всі етапи ділення записуються таким чином: в центральній колонці – ділене число, в правій колонці – дільник (кожного разу – це основа с\ч Q), в лівій колонці – залишок від ділення. Отримана частка стає діленим наступного етапу і знов ділиться на Q, залишок знов записується в ліву колонку. Процедура продовжується до тих пір, поки частка не стане рівна одиниці. Залишки від ділення на Q виписуються в порядку, зворотному їх отриманню (від низу до верху);

2) дробова частина числа переводиться шляхом поетапного множення на Q. В двох колонках всі етапи множення записуються таким чином: в правій колонці – множене дробове число і під ним множник - Q, в лівій колонці – ціла частина. На першому етапі цілої частини немає, тому зліва від дробового числа, що переводиться, можна або написати 0 з десятковою крапкою, або не писати нічого. На наступних етапах під цілою частиною мається на увазі число з розряду результату, більш старшого, ніж старший розряд множеного (це може бути 1 або, за відсутності перевищення, 0). Процедура продовжується до тих пір, поки дробова частина не стане рівною нулю (наприклад, при перекладі числа 0.25, але це не завжди можливо). Цілі частини виписуються після коми в порядку їх отримання (зверху вниз, без 0 першого етапу). Результатом може бути або кінцевий, або періодичний дріб. Тому, коли дріб є періодичним, доводиться обривати множення на якому-небудь кроці і задовольнятися наближеним записом початкового числа в системі з основою Q.

Візьмемо, наприклад, число 137,285.

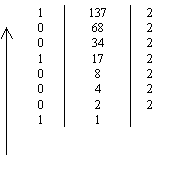
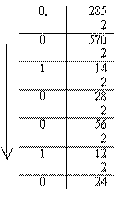
137,285₍₁₀₎ = 10001001,0100101 ... _(2).

При переведенні чисел із системи числення з основою Q в десяткову с\ч необхідно пронумерувати розряди цілої частини справа наліво, починаючи із нульового, і в дробовій частині, починаючи із розряду відразу після коми зліва направо (початковий номер -1). Потім обчислити суму добутків відповідних значень розрядів на основу с\ч в степені, рівній номеру розряду. Це і є представлення початкового числа в десятковій с\ч.

При переведення чисел із двійкової в десяткову с\ч можуть бути корисними наступні таблиці 1.3 та 1.4 (для прискорення одноманітних розрахунків).

Таблиця 1.3 - Деякі додатні степені числа 2 (в десятковій с\ч)

Показник

Степінь

Таблиця 1.4 - Деякі від'ємні степені числа 2 (в десятковій с\ч)

Показник	-1	-2	-3	-4	-5	-6	-7
Степінь	0,5	0,25	0,125	0,0625	0,03125	0,015625	0,0078125

Розглянемо декілька прикладів переведення цілого двійкового числа в десяткову систему числення.

а) 1000001₍₂₎=1 * 2⁶+0 * 2⁵+0 * 2⁴+0 * 2³+0 * 2²+ 0 * 2¹+1 * 2⁰ = 64+1 = 65₍₁₀₎.

б) 1011001₍₂₎ = 1 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 1 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰ = 64 + 0 + 16 + 8 + 0 + 0 + 1 = 89₍₁₀₎.

Очевидно, що якщо в якому-небудь розряді стоїть нуль, то відповідний доданок можна опускати.

Розглянемо, як переводиться правильна двійкова дріб в десяткову:

а) 0,100111₍₂₎ = 1 * 2^-1 + 0 * 2^-2 + 0 * 2^-3 + 1 * 2^-4 + 1 * 2^-5 + 1 * 2^-6 = 0,5 + 0 + 0 + 0,0625 + 0,03125 + 0,015625 = 0,609375₍₁₀₎.

б) 1000011111,0101₍₂₎=1 * 2⁹ + 1 * 2⁴ + 1 * 2³ + 1 * 2² + 1 * 2¹ + 1 * 2⁰ + 1 * 2^-2 + 1 * 2^-4 = 512 + 16 + 8 + 4 + 2 + 1 + 0,25 + 0,0625 = 543,3125₍₁₀₎.

З числами в інших с\ч можна виконувати всі 4 арифметичні дії.

Виконуються вони аналогічно діям в десятковій системі. Для виконання арифметичних операцій в с\ч з основою Q = 2 необхідно враховувати наступні правила.

Додавання:

0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10 (одиниця йде в старший разряд).

Віднімання:

0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (одиницю забираємо у старшого розряду).

Множення:

0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1.

Ділення:

0: 0 = не визначено, 1: 0 = не визначено, 0: 1 = 0, 1: 1 = 1.

Знайдіть суму доданків:

а) 10000000100₍₂₎ + 111000010₍₂₎ = 10111000110₍₂₎.

Виконаємо перевірку результатів розрахунків переведенням в десяткову систему числення. Для цього переведемо кожний доданок і суму в десяткову систему числення, виконаємо складання доданків в десятковій системі числення. Результат повинен співпасти з сумою.

10000000100₍₂₎ = 1 * 2¹⁰+1 * 2² = 1024+4 = 1028₍₁₀₎

111000010₍₂₎ = 1 * 2⁸+ 1 * 2⁷+ 1 * 2⁶+ 1 * 2¹ = 256+128+64+2 = 450₍₁₀₎

10111000110₍₂₎ = 1 * 2¹⁰+ 1 * 2⁸+ 1 * 2⁷+ 1 * 2⁶+ 1 * 2²+ 1 * 2¹ = 1024+256+128+64+4+2 = 1478₍₁₀₎

1028₍₁₀₎ + 450₍₁₀₎ = 1478₍₁₀₎

Результати співпадають, отже, обчислення в двійковій системі числення виконані вірно.

б) 100110₍₂₎ +110110₍₂₎ = 1011100₍₂₎.

Знайти різницю між двома числами:

а) 1010001₍₂₎ - 101011₍₂₎ = 100110₍₂₎.

б) 1100000011,011₍₂₎ - 101010111,1₍₂₎ = 110101011,111₍₂₎.

Знайти добуток множників:

а) 1001₍₂₎ * 1011₍₂₎ = 1100011₍₂₎.

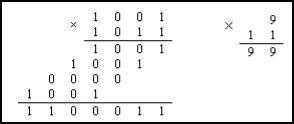
б) 100111₍₂₎ * 1000111₍₂₎ = 101011010001₍₂₎.

Знайти частку чисел:

а) 110010₍₂₎ \ 1010₍₂₎ = 101₍₂₎.

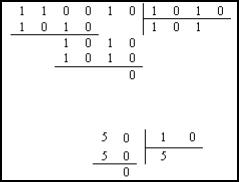
б) 100110010011000₍₂₎ \ 101011₍₂₎=111001000₍₂₎.

Якщо необхідно перевести число з двійкової системи числення в систему числення, основою якої є степінь двійки, достатньо об'єднати цифри двійкового числа в групи по стільки цифр, який показник степені, і використовувати приведений нижче алгоритм. Наприклад, якщо переклад здійснюється у восьмеричну систему, то групи міститимуть три цифри. Отже, в цілій частині проводитимемо угрупування справа наліво, в дробовій — зліва направо. Якщо в останній групі бракує цифр, дописуємо нулі: в цілій частині — зліва, в дробовій — справа. Потім кожна група замінюється відповідною цифрою нової системи. Відповідності груп приведені в таблицях 1.5, 1.6, 1.7.

Таблиця 1.5 – Відповідність груп цифр двійкової та вісімкової с\ч

P

Таблиця 1.6 – Відповідність груп цифр двійкової та шістнадцяткової с\ч

P

A

B

C

D

E

F

Таблиця 1.7 – Відповідність груп цифр шістнадцяткової та десяткової с\ч

P

A

B

C

D

E

F

Переведемо з двійкової системи у восьмеричну число 1111010101,11₍₂₎.

001111010101, 110 ₍₂₎ = 1725,6₍₈₎.

Переведемо з двійкової системи в шістнадцяткову число 1111010101,11₍₂₎.

001111010101, 1100 ₍₂₎ = 3D5,C₍₁₆₎.

Наведемо приклад представлення десяткового дробового числа в різних системах числення: 179,625₍₁₀₎ = В3,А₍₁₆₎ = 10110011,1010₍₂₎ = 263,5₍₈₎.

1.2.3. Поняття інформатизації, інформатизація суспільства

Розвиток науки, обчислювальної техніки і розвиток інформаційного суспільства є взаємозалежними. Як суспільство проходило певні етапи – первіснообщинний, рабовласницький, феодальний, так і обчислювальна техніка розвивалася поетапно. Протягом всієї передуючої XX століттю історії розвитку людської цивілізації основним предметом праці залишалися матеріальні об'єкти. Діяльність за межами матеріального виробництва і обслуговування, як правило, відносилася до категорії непродуктивних витрат.

Революційні зміни в області інформаційних основ суспільства відбувалися в результаті виникнення писемності, а потім і книгодрукування. Проте вони не зачіпали найважливішій компоненти інформаційних процесів - переробки інформації.

Зараз вчені виділяють ознаки інформаційного суспільства. Інформаційне суспільство - це суспільство, в якому як головні фактори виробництва виступають фактори ідеальні: знання і інформація. Неможливість розвиватися в одному темпі з інформаційними технологіями можна розглядати як джерело нового виду дискримінації, широко використовується на дипломатичному рівні по відношенню до тих або інших прошарків суспільства або до громадян тієї або іншої країни термін «інформаційна нерівність». Якщо винахід друкарської книги зробив необхідним для члена суспільства уміння читати, то використовування інформаційних технологій в суспільстві зобов'язало уміти поводитися з електронною інформацією, розосередженою по загальносвітовій інформаційній мережі. В деякому роді, в світовій спільноті починається компанія по ліквідації неписьменності, і кількість комп'ютерно-грамотних людей з часом стане таким же важливим показником розвитку країни, як кількість людей, що уміють читати і писати.

1.3. Еволюція обчислювальної техніки і інформаційних технологій

1.3.1. Історія розвитку обчислювальної техніки

Першими рахунковими пристроями, прообразами сучасних комп'ютерів, були китайські рахівниці, створені більше 6 тисяч років тому.

Перша обчислювальна машина була створена в 1642 році французьким математиком і фізиком Блезом Паскалем (1623-1662). Вона могла лише виконувати елементарні арифметичні дії – складання і віднімання.

В 1694 році німецький учений, математик Фон Лейбніц (1646 – 1716) створив обчислювальну машину, яка виконувала вже 4 арифметичні дії. Її зараз розглядають як спробу створення алгебри логіки.

В 1770 році Якобсон створив обчислювальну машину, здатну працювати з п'ятизначним числом.

В 1801 році Жакар створив автоматичний ткацький верстат, як програма для якого була використана перфорована карта.

Англійський вчений Ч. Беббедж запропонував використовувати програми з метою автоматизації обчислень. В 1823 році їм була створена різницева машина по перевірці і складанню математичних таблиць.

З 1833 по 1871 рр. Беббедж створював механічну цифрову обчислювальну машину, названу згодом аналітичною машиною Беббіджа. Це була аналітична машина по перевірці і складанню математичних таблиць.

В 1854 році Буль створив алгебру логіки, яка згодом знайшла застосування в ПК і з'явилася дуже важливою умовою і передумовою розвитку схемотехніки.

В 1866 році американський вчений Холмріт створив перфокарткову систему. Його комп'ютер використовував електричні сигнали.

В 1930 році Буш створив різницевий аналізатор - аналоговий обчислювальний пристрій для вирішення диференціальних рівнянь.

В 1935 році Зусе створив механічну машину Z1, яка виконувала двійкові операції.

В 1936 році Тюрінг створив так звану «машину Тюрінга», що була теоретичною системою для обчислень.

В 1938 році Клод Шеннон винайшов двійкові схеми перемикачів. Проводився аналіз релейних схем перемикачів.

Найбільш активізувався процес створення обчислювальних машин (ОМ) в 40-х роках, причому подібні ОМ створювалися часто паралельно в країнах Європи, в СРСР і в США. До того ж в умовах другої світової війни, по-перше, всі що брали участь в ній країни збільшили фінансування наукоємких виробництв, у тому числі і в області експериментів по створенню ОМ. І, по-друге, в науково-дослідних лабораторіях і університетах США працювала безліч учених-емігрантів, що бігли від нацистського режиму, як з Німеччини, так і з інших країн, а в секретних лабораторіях Німеччини, у свою чергу, працювали як учені-нацисти, так і учені, просто вимушені працювати ради порятунку свого життя. Таким чином, була велика вірогідність так званого симбіозу досліджень, що проводилися в одному напрямі на основі подібних вхідних можливостей.

В розвитку ОМ виділяють п'ять поколінь. В основу класифікації закладена елементна база, на якій будуються ОМ.

В 1943 році були створені обчислювальні машини першого покоління на базі електронних ламп.

В 1943 році Блетчлі створив Colossus-1 - перший електронний комп'ютер.

В 1943 році в Гарвардському університеті була створена машина МARK-1, в якій використовувалися електромагнітні реле.

В 1943 - 1946 рр. Еккерт Мауклі створив машину, що вважається першим комп'ютером – ЕNIAC. Цей електронний комп'ютер міг виконувати 5000 операцій складання в секунду.

В 1947 році Фон Нейман створив машину EDVAC, що стала поворотним пунктом в конструювання комп'ютерів.

В 1948 році Манчестерський університет створив більш пізній комерційний варіант машини MARK-1 фірми FERRANTI.

Перше покоління електронних обчислювальних машин (ЕОМ), таких, як EDSAC і Colossus, було громіздким, ненадійним, побудовані на лампах, вони потребували холодильних установках. На цій стадії почалася розробка програмного забезпечення (наприклад, операційна система ЕОМ EDSAC)

В 1948 році в Bell Telephone Laboratories (США) був винайдений транзистор - основа для комп'ютерів другого (після лампового) покоління.

Друге покоління (50 – 60 р.р.) комп'ютерів побудовано на базі напівпровідникових елементів (транзисторах).

В 1949 році в Кембріджському університеті була створена машина EDSAC. Її програмним нововведенням була наявність операційної системи.

В 1954 - 1957 рр. фірмою NCR був створений комп'ютер NCR 304 - перший комп'ютер на транзисторах.

В 1959 році фірмою IBM була створена найбільш поширена в світі транзисторна ЕОМ IBM 1401.

До другого покоління ЕОМ відносять, наприклад, IBM 1401 і NCR 304, які будувалися на транзисторах, винайдених Шокле, Бардіним, Браттеном, співробітниками Bell Telephone Laboratories.

В 1956 році Дартмунд коледж зайнявся розробкою «Штучного інтелекту». «Штучному інтелекту» належить зайняти центральне місце в машинах п'ятого покоління.

В 1957 році Ньюелл Шоу Саймон створив загальний «вирішувач задач» - основу для важливих розробок в області «Штучного інтелекту».

В 1960 році фірма DEC створила PDP 8 - перший міні комп'ютер.

Основна елементна база комп'ютерів третього покоління (60 –
70 р.р.) - інтегральні схеми малої і середньої інтеграції.

В 1968 році фірмою IBM створила комп'ютерну серію ЕОМ IBM/360 і IBM/370 – на монолітних інтегральних схемах.

Третє покоління IBM/360 і ICL 1900 створювалися на базі інтегральних схем: транзистори, резистори, конденсатори і діоди розміщувалися в межах поверхневого десятимікронного шару кремнієвої пластини. Компоненти з'єднувалися шаром металу, напилюваного на таку пластину, причому ті, що вимагаються межсоединения забезпечувалися шляхом відповідного витравляння матеріалу. На цій стадії були розроблені мови програмування високого рівня (Кобол, Фортран) і складні операційні системи.

Характерним представником машин цього класу є ЄС ЕОМ.

Єдина система електронних обчислювальних машин (ЄС ЕОМ) є сімейством програмно сумісних машин третього покоління.

Кожна модель ЄС ЕОМ мала базовий набір зовнішніх пристроїв. Наприклад, ЄС 1050 мала:

- 5 накопичувачів на магнітних дисках;

- 8 накопичувачів на магнітних стрічках;

- 2 контролери для дисків і стрічок;

- 2 пристрої введення з перфокарт;

- 1 пристрій введення з перфострічок;

- 2 пишучі машинки;

- 2 пристрої підготовки даних на перфокартах і перфострічках.

В комп'ютерах четвертого покоління (70 – по н/в) застосовані великі інтегральні схеми БІС (мікропроцесори). Застосування мікропроцесорів в ЕОМ дозволило створити персональний комп'ютер (ПК), відмітною особливістю якого є невеликі розміри і низька вартість.

В 1971 році фірма Intel випустила мікропроцесор – це була перша серйозна принципова розробка в мікроелектроніці.

В 1972 році фірма Unimation з'явилася першою компанією по виробництву промислових роботів

Четверте покоління з початку 80-х років характерний підвищеним ступенем інтеграції мікросхем з використанням технології СБІС (надвеликих інтегральних схем). На цьому етапі вводиться різні архітектурні і програмні новини.

Мікропроцесори революціонізували обчислювальну техніку. Вона стала більш дешевою, масовою і надійною, а її застосування економічно ефективно практично у всіх областях.

П'яте покоління комп'ютерів – це сучасний етап їх розвитку.

Відмінні риси:

- нові технології виробництва;

- відмова від традиційних мов програмування на користь мов з підвищеними можливостями маніпулювання символами і з елементами логічного програмування (так звані мови штучного інтелекту, такі, як, наприклад, Пролог);

- акцент на нову архітектуру (наприклад, на архітектуру потоку даних);

- нові способи уведення-виведення, зручні для користувача (наприклад, розпізнавання мови і образів, синтез мови, обробка повідомлень на природній мові);

- штучний інтелект (тобто автоматизація процесів рішення задач, отримання висновків, маніпулювання знаннями).

1.3.2. Архітектура обчислювальної системи

Типова архітектура мікропроцесорної системи.

Під архітектурою комп'ютера розуміється загальна конфігурація основних компонент, їх головні спроможності і характеристики, а також взаємозв'язок. Загальна архітектура типової мікросистеми представлена на рисунку 1.1.

Дата добавления: 2015-05-24