Ряди даних. 2 страница

Наприклад:

Пусть A1=X

Тогда B1=У=ЕСЛИ(A1=0; 5; -10)

При конструюванні складніших перевірок у якості значень аргументів арг1 і арг2 можуть бути вкладені до семі функцій ЕСЛИ.

На прикладах з'ясуємо, чи є логічні значення ИСТИНА і ЛОЖЬ
відповідно 1 і 0.

Значення ИСТИНА не є числом “1” при використанні в умовах, тому, коли, наприклад, в чарунці А3 знаходиться число “1”, результатом роботи формули виду:

=ЕСЛИ(A3=ИСТИНА; ИСТИНА; ЛОЖЬ)

буде логічне значення ЛОЖЬ.

В той же час результатом роботи формули вигляду:

=ЕСЛИ(A3=1; ИСТИНА; ЛОЖЬ)

буде логічне значення ИСТИНА.

Проте при арифметичних діях логічне значення ИСТИНА поводиться як число “1”. Наприклад, якщо в чарунці А1 знаходиться логічне значення ИСТИНА, а в чарунці B1 — від’ємне число -5, то результатом формули “=A1+B1” буде число -4, а результатом добутку “=A1*B1” буде число -5.

Аналогічно, логічне значення ЛОЖЬ не є числом “0”, але в арифметичних діях поводиться як число “0”.

Функція НЕ(арг) змінює на протилежне логічне значення свого аргументу. Вона часто використовується в тих випадках, коли необхідно бути упевненим в тому, що значення не рівно деякій величині.

Аргумент функції арг — це значення або вираз, результатом обчислення якого є ИСТИНА або ЛОЖЬ. Якщо арг має значення ЛОЖЬ, то функція НЕ повертає значення ИСТИНА, а якщо арг має значення ИСТИНА, то функція НЕ повертає значення ЛОЖЬ.

Наведемо два прості приклади використання функції НЕ.

Формула “ =НЕ(D7) ” повертає ИСТИНА тільки у тому випадку, коли в чарунці D7 знаходиться 0. На додатні і від’ємні числа формула “ =НЕ(D7) ” повертає ЛОЖЬ.

Формула “ =НЕ(D8>1,5) ” повертає ИСТИНА, коли в чарунці D8 знаходиться число менше або рівне 1,5 і повертає ЛОЖЬ, коли в чарунці D7 знаходиться число, що перевищує 1,5.

Функції И(арг1, арг2...) і ИЛИ(арг1, арг2...)

Функція И(арг1, арг2...) повертає значення ИСТИНА, якщо всі аргументи мають значення ИСТИНА і повертає значення ЛОЖЬ, якщо хоча б один аргумент має значення ЛОЖЬ.

Матриця можливих наборів для функції И:

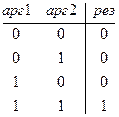
Функция ИЛИ(арг1, арг2,...) повертає значення ИСТИНА, якщо хоча б один аргумент має значення ИСТИНА.

Матриця можливих наборів для функції ИЛИ:

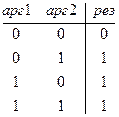
Аргументи арг1, арг2,... повинні бути логічними значеннями, масивами або посиланнями, які містять логічні значення. Якщо аргумент, який є посиланням або масивом, містить тексти або порожні чарунки, то такі значення ігноруються. Якщо вказаний інтервал не містить логічних значень, повертається значення помилки #ЗНАЧ!.

Розглянемо приклади використовування функції И(арг1, арг2...).

Припустимо, що вам потрібно вивести на екран вміст чарунки A4, якщо вона містить число строго між 1 і 100 і повідомлення “Значення зовні інтервалу” - в іншому випадку. Тоді, якщо чарунка A4 містить число 104, то формула

=ЕСЛИ(И(1<A4;A4<100);A4;”Значение зовні інтервалу”)

повертає вираз “Значення зовні інтервалу”, а якщо чарунка A4 містить число 50, то формула повертає число 50.

Формула

=И(C10;C8>1,35)

повертає значення ИСТИНА при всіх числах, що задовольняють умові C8>1,35 незалежно від числа, яке знаходиться в чарунці C10 (додатне, від’ємне або 0). Якщо в осередку C10 знаходиться значення ЛОЖЬ, то тоді ця формула повертає значення ЛОЖЬ. Якщо умова C8>1,35 не виконується, то також повертається ЛОЖЬ.

Формула

=И(C10>0;C8>1,35)

повертає значення ИСТИНА при всіх числах, що знаходяться в чарунках C8 і C10, які задовольняють умовам C8>1,35 і C10>0.

Розглянемо приклади використовування функції ИЛИ(арг1, арг2...).

Якщо в чарунці A1 міститься значення ИСТИНА, в чарунці A2 - ЛОЖЬ, а в чарунці A3 - ИСТИНА, то результатом роботи формули

=ИЛИ(A1:A3)

буде ИСТИНА. Якщо в чарунках А1, А2 і А3 буде ЛОЖЬ, то формула видасть ЛОЖЬ.

2.2.6 Створення діаграм в MS Excel

В Microsoft Excel є можливість графічного представлення даних у вигляді діаграм. Діаграми - цей зручний засіб графічного представлення даних. Вони дозволяють оцінити наявні величини краще, ніж найуважніше вивчення кожної чарунки робочого листа. Діаграма може допомогти знайти помилку в даних.

Ехсеl підтримує 14 типів різних стандартних двух- і тривимірних діаграм. При створенні нової діаграми за умовчанням в Excel встановлена гістограма.

Для того, щоб можна було побудувати діаграму, необхідно мати, принаймні, один ряд даних. Джерелом даних для діаграми виступає таблиця Excel.

Діаграми пов'язані з даними листа, на основі яких вони були створені, і змінюються кожного разу, коли змінюються дані на листі.

Діаграми можуть використовувати дані несуміжних чарунок. Діаграма може також використовувати дані зведеної таблиці.

Можна створити або упроваджену діаграму, або лист діаграми. Упроваджена діаграма – це об'єкт, розташований на листі і такий, що зберігається разом з листом при збереженні книги. Лист діаграми – це лист книги, що містить тільки діаграму.

Спеціальні терміни, вживані при побудові діаграм.

Вісь X називається віссю категорій і значення, що відкладаються на цій осі, називаються категоріями.

Значення, що відображаються в діаграмі, складають ряди даних. Ряд даних – послідовність числових значень. При побудові діаграми можуть використовуватися декілька рядів даних. Всі ряди повинні мати одну й ту ж саму розмірність.

Легенда – розшифровка позначень рядів даних на діаграмі.

Тип діаграми впливає на її структуру і пред'являє певні вимоги до рядів даних. Так, для побудови кругової діаграми завжди використовується тільки один ряд даних, але при цьому ще як мінімум один ряд значень – для підписів і \ або легенди (див. рис. 2.13).

Рисунок 2.13 – Майстер побудови кругової діаграми

Майстер діаграм.

1. Виділіть в таблиці діапазон даних, по яких будуватиметься діаграма, включаючи, якщо це можливо, і діапазони підписів до цих даних по рядках і стовпцях.

2. Для того, щоб виділити декілька несуміжних діапазонів даних, проводьте виділення, утримуючи клавішу Ctrl. Виділені несуміжні діапазони повинні утворювати прямокутник.

3. Викличте майстер побудови діаграм (пункт меню Вставка/ Диаграма або кнопка на стандартній панелі інструментів).

4. Уважно читаючи всі закладки діалогового вікна майстра побудови діаграм на кожному кроці, дійдіть до кінця (вибирайте “ Далее ”, якщо ця кнопка активна) і у результаті натисніть “ Готово ”.

Після побудови діаграми можна змінити:

· розміри діаграми, потягнувши за габаритні позначення, які з'являються тоді, коли діаграма виділена;

· положення діаграми на листі, шляхом перетягування об'єкту діаграми мишею;

· шрифт, колір, положення будь-якого елемента діаграми, двічі клацнувши по цьому елементу лівою кнопкою миші;

· тип діаграми, початкові дані, параметри діаграми, вибравши відповідні пункти з контекстного меню (права кнопка миші).

Діаграму можна видалити: виділити і натиснути Delete.

Діаграму, як текст і будь-які інші об'єкти в MS Office, можна копіювати в буфер обміну і вставляти в будь-який інший документ.

2.3 Додаткові можливості аналізу даних

2.3.1 Пошук рішення

Пошук значення чарунки, відповідній екстремальному значенню залежної чарунки.

Процедуру пошуку рішення можна використовувати для визначення значення впливаючої чарунки, яке відповідає екстремуму залежної чарунки - наприклад, витрати на рекламу, що забезпечують максимальний прибуток. Впливаюча і цільова чарунки повинні бути зв'язані формулою листа, інакше при зміні значення одній не змінюватиметься інша.

Створення моделі для пошуку рішення.

Процедура пошуку рішення дозволяє знайти оптимальне значення формули, що міститься в чарунці, яка називається цільовою. Ця процедура працює з групою чарунок, прямо або побічно пов'язаних з формулою в цільовій чарунці. Щоб отримати по формулі, що міститься в цільовій чарунці, заданий результат, процедура змінює значення у впливаючих чарунках. Щоб звузити безліч значень, що використовуються в моделі, застосовуються обмеження. Ці обмеження можуть посилатися на інші впливаючі чарунки.

Постановка задачі і оптимізація моделі за допомогою процедури пошуку рішення.

В меню Сервис виберіть команду Поиск решения.

Якщо команда Поиск решения відсутня в меню Сервис, встановіть відповідну надбудову.

В полі „Установить целевую ячейку” введіть адресу або ім'я чарунки, в якій знаходиться формула моделі, що оптимізується.

Щоб максимізувати значення цільової чарунки шляхом зміни значень впливаючих чарунок, встановіть перемикач в положення „максимальному значению” (див. рис. 2.14).

Рисунок 2.14 –Вікно „Поиск решения”

Щоб мінімізувати значення цільової чарунки шляхом зміни значень впливаючих чарунок, встановіть перемикач в положення „минимальному значению”.

Щоб встановити значення в цільовій чарунці рівним деякому числу шляхом зміни значень впливаючих чарунок, встановіть перемикач в положення „значению” і введіть у відповідне поле необхідне число.

В полі „Изменяя ячейки” введіть імена або адреси змінних чарунок, розділяючи їх комами. Можна вказати прямо на листі, які чарунки потрібно змінювати, за допомогою кнопки . Змінні чарунки повинні бути прямо або побічно пов'язані з цільовою чарункою (це і є впливаючі чарунки). Допускається установка до 200 змінних чарунок.

Щоб автоматично знайти всі чарунки, що впливають на формулу моделі, натисніть кнопку Предположить.

В списку „Ограничения” введіть всі обмеження, що накладаються на пошук рішення(див. рис. 2.15).

Рисунок 2.15 – Додавання обмежень у вікні “Поиск решения”

Натисніть кнопку Выполнить (див. рис. 2.16).

Рисунок 2.16 – Вікно “Поиск решения” підготоване для запуску пошуку на виконання

Щоб зберегти знайдене рішення, встановіть перемикач в діалоговому вікні Результати поиска решения в положення „Сохранить найденное решение”.

Щоб відновити початкові дані, встановіть перемикач в положення „Восстановить начальные значения”.

2.3.2 Консолідація даних

Консолідація даних по розташуванню.

1. Вкажіть верхню ліву чарунку кінцевої області даних, що консолідуються.

2. В меню Данные виберіть команду Консолидация.

3. Виберіть із списку, що розкривається, функцію, яку слід використовувати для обробки даних.

4. Введіть в полі Ссылка вихідну область даних, що консолідуються.

5. Натисніть кнопку Добавить.

6. Повторіть кроки 4 і 5 для всіх початкових областей, що консолідуються. Щоб автоматично обновляти підсумкову таблицю при зміні джерел даних, встановіть прапорець „Создавать связи с исходными данными”.

Зв'язки не можна використовувати, якщо початкова область і область призначення знаходяться на одному листі. Після установки зв'язків не можна додавати нові початкові області і змінювати початкові області, що вже входять в консолідацію.

При консолідації даних по розташуванню заголовки категорій початкових областей не копіюються автоматично в область призначення. Якщо в області призначення вимагається розмістити заголовки, скопіюйте або введіть їх вручну.

Консолідація даних по категоріях.

1. Вкажіть верхню ліву чарунку кінцевої області даних, що консолідуються.

2. В меню Данные виберіть команду Консолидация.

3. Виберіть із поля зі списком Функция функцію, яку слід використовувати для обробки даних.

4. Введіть вихідну область даних, що консолідуються, в полі Ссылка. Переконайтеся, що початкова область має заголовок.

5. Натисніть кнопку Добавить.

6. Повторіть кроки 4 і 5 для всіх початкових областей, що консолідуються. В наборі прапорців Использовать в качестве имен встановите прапорці, відповідні розташуванню в початковій області заголовків: у верхньому рядку, в лівому стовпці або у верхньому рядку і в лівому стовпці одночасно. Щоб автоматично обновляти підсумкову таблицю при зміні джерел даних, встановіть прапорець Создавать связи с исходными данными.

Зв'язки не можна використовувати, якщо початкова область і область призначення знаходяться на одному листі. Після установки зв'язків не можна додавати нові початкові області і змінювати початкові області, вже що входять в консолідацію.

Якщо мітки в одній з початкових областей не співпадають з мітками в інших початкових областях, то при консолідації даних для них будуть створені окремі рядки або стовпці.

2.3.3 Апроксимація експериментальних даних. Лінії тренда

На практиці часто доводиться стикатися із задачею про згладжування експериментальної залежності або задачею апроксимації.

АПРОКСИМАЦІЯ (від лат. Approximo - наближаюся) - заміна одних математичних об'єктів (напр., чисел або функцій) іншими, більш простими і в тому або іншому значенні близькими до початкових (напр., кривих ліній близькими до них ламаними).

АПРОКСИМАЦІЯ - наближене рішення складної функції за допомогою більш простих, що різко прискорює і спрощує рішення задач. В економіці метою апроксимації часто є укрупнення характеристик модельованих економічних об'єктів.

Апроксимацією називається процес підбору емпіричної формули 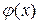для встановленої з досвіду функціональної залежності у=f(x). Емпіричні формули служать для аналітичного представлення експериментальних даних.

Звичайно задача апроксимації розпадається на дві частини. Спочатку встановлюють вид залежності у = f(х) і, відповідно, вид емпіричної формули, тобто вирішують, чи є вона лінійною, квадратичною, логарифмічною або якою-небудь іншою. Після цього визначаються чисельні значення невідомих параметрів вибраної емпіричної формули, для яких наближення до заданої функції виявляється якнайкращим. Якщо немає яких-небудь теоретичних міркувань для підбору виду формули, звичайно вибирають функціональну залежність з числа найпростіших, порівнюючи їх графіки з графіком заданої функції.

Після вибору вигляду формули визначають її параметри. Для якнайкращого вибору параметрів задають міру близькості апроксимації експериментальних даних. У багатьох випадках, особливо якщо функція f(x) задана графіком або таблицею (на дискретній безлічі точок), для оцінки ступеня наближення розглядають різниці 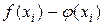для точок 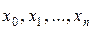. Існують різні міри близькості і, відповідно, способи рішення цієї задачі. Деякі з них дуже прості, швидко приводять до результату, але результат цей є сильно наближеним. Інші більш точні, але і складніші.

В найпростішому випадку задача апроксимації експериментальних даних виглядає таким чином.

Хай є якісь дані, отримані практичним шляхом (в ході експерименту або спостереження), які можна представити парами чисел (х; у). Залежність між ними відображає таблиця 2.7.

Таблиця 2.7 – Залежність експериментальних X та Y

Х	Х1	X2	...	Хn
Y	Y1	Y2	...	Yn

На основі цих даних потрібно підібрати функцію y = f(х), яка найкращим образом згладжувала б експериментальну залежність між змінними і по можливості точно відображала загальну тенденцію залежності між х і у, виключаючи погрішності вимірювань і випадкові відхилення. Це значить, що відхилення в якомусь значенні були б якнайменшими.

З'ясувати вид функції можна або з теоретичних міркувань, або аналізуючи розташування точок (х_п; у_п) на координатній площині.

Наприклад, хай точки розташовані так, як показано на рис. 2.17.

Рисунок 2.17 - Можливий варіант розташувань експериментальних точок

Враховуючи те, що практичні дані отримані з деякою погрішністю, обумовленою неточністю вимірювань, необхідністю округлення результатів і т. п., природно припустити, що тут має місце лінійна залежність у = ах + b.

Щоб функція прийняла конкретний вигляд, необхідно якимсь чином обчислити а і b.

Розташування експериментальних точок у вигляді кривої на рис. 2.18 наводить на роздуми, що залежність зворотно пропорційна і функцію 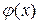потрібно підбирати у вигляді у = а + b/х. Тут також необхідно обчислити параметри а і b.

Рисунок 2.18 Інший варіант розташування експериментальних крапок

Таким чином, розташування експериментальних точок може мати самий різний вигляд, і кожному відповідає конкретний тип функції.

Побудова емпіричної функції зводиться до обчислення параметрів, що в неї входять, так щоб зі всіх функцій такого вигляду вибрати ту, яка краще за інші описує залежність між величинами, що вивчаються. Тобто сума квадратів різниці між табличними значеннями функції в деяких точках і значеннями, обчисленими по отриманій формулі, повинна бути мінімальною.

В MS Excel апроксимація експериментальних даних здійснюється шляхом побудови їх графіка (х — абстрактні величини) або точкового графіка (х — має конкретні значення) з подальшим підбором відповідної апроксимуючої функції (лінії тренда). Можливі наступні варіанти функцій:

1. Лінійна — у = ах + b. Звичайно застосовується в найпростіших випадках, коли експериментальні дані зростають або убувають з постійною швидкістю.

2. Поліноміальна —у=а₀ + a₁x²+a₂х² +... + а_nхⁿ, де до шостого порядку включно (n <= 6), a_i — константи. Використовується для опису експериментальних даних, поперемінно зростаючих і убуваючих. Ступінь полінома визначається кількістю екстремумів (максимумів або мінімумів) кривої.

Поліном другого ступеня може описати тільки один максимум або мінімум,
поліном третього ступеня може мати один або два екстремуми, четвертого ступеня — не більше трьох екстремумів і т. д.

3. Логарифмічна — у=a ln x + b, де а і b — константи, ln —функция натурального логарифма. Функція застосовується для опису експериментальних даних, які спочатку швидко ростуть або убувають, а потім поступово стабілізуються.

4. Степенева — у = bx^a, де а і b — константи. Апроксимація степеневою функцією використовується для експериментальних даних, з швидкістю росту, що постійно збільшується (або убуває). Дані не повинні мати нульових або від’ємних значень.

5. Експоненціальна — у= be^ax, де а і b — константи, е — основа натурального логарифма. Застосовується для опису експериментальних даних, які швидко ростуть або убувають, а потім поступово стабілізуються. Часто її використання витікає з теоретичних міркувань.

Ступінь близькості апроксимації експериментальних даних вибраною функцією оцінюється коефіцієнтом детермінації (R2). Таким чином, якщо є декілька відповідних варіантів типів апроксимуючих функцій, можна вибрати функцію з більшим коефіцієнтом детермінації (який прагне до 1).

Для здійснення апроксимації на діаграмі експериментальних даних необхідно клацанням правої кнопки миші викликати контекстне меню і вибрати пункт Добавить линию тренда. В діалоговому вікні Линия тренда, на вкладці Тип вибирається вид апроксимуючої функції, а на вкладці Параметры задаються додаткові параметри, що впливають на відображення апроксимуючої кривої.

Приклад.

Припустимо, отриманий графік експериментальних даних (див. таблицю 2.8).

Таблиця 2.8 – Експериментальні дані (зміна з часом рівня виробництва)

Рік
Виробництво	17.1	18.0	18.9	19.7	19.7	20.0	20.2	20.5	20.7	20.9	21.5

Здійснимо апроксимацію отриманою кривою полиномиальною функцією другого порядку, оскільки крива досить гладка і не сильно відрізняється від прямої лінії. Для цього покажчик миші встановлюємо на одну з точок графіка і клацаємо правою кнопкою. В контекстному меню, що з'явилося, вибираємо пункт Добавить линию тренда. З'являється діалогове вікно Линия тренда (рис. 2.19).

В цьому вікні на вкладці Тип вибираємо тип лінії тренда — Полиномиальная і встановлюємо ступінь - 2.

Рисунок 2.19 - Вкладка Тип діалогового вікна Линия тренда

Потім відкриваємо вкладку Параметры (рис. 2.20) і встановлюємо прапорці в поля „показывать уравнение на диаграмме” і „поместить на диаграмму величину достоверности аппроксимации (R^{^}2)”. Після чого потрібно клацнути на кнопці ОК. В результаті отримаємо на діаграмі апроксимуючу криву (рис. 2.21).

Як видно з рис. 2.21, рівняння найкращої поліноміальної апроксимуючої функції для деяких абстрактних значень х (1, 2,3...) виглядає як

Y = -0,0425x² + 0,8569x + 16,507

При цьому точність апроксимації достатньо висока — R² = 0,9736.

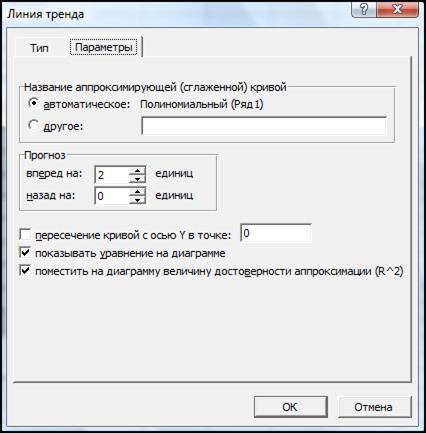
Рисунок 2.20 - Вкладка Параметры діалогового вікна Линия тренда

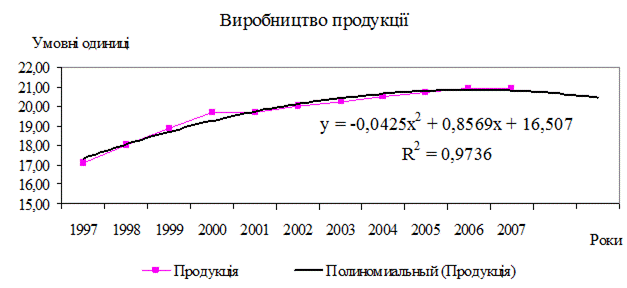
Рисунок 2.21 - Експериментальні дані з апроксимацією поліноміальною кривою

Спробуємо поліпшити якість апроксимації вибором іншого типу функції (можливо, більш адекватного). Тут можливим варіантом представляється логарифмічна функція. Для цього повторюємо попередні операції, за винятком того, що у вікні Линия тренда на вкладці Тип вибираємо тип лінії тренда — Логарифмическая.

В результаті отримаємо інший варіант апроксимації — логарифмічною кривою (рисунок 2.22). Бачимо, що рівняння найкращої поліноміальної апроксимуючої функції дещо поступається по точності апроксимації логарифмічній кривій — R² = 0,9736 < 0,9876. Тому, якщо немає яких-небудь теоретичних міркувань, то можна вважати, що найкращою апроксимацією є апроксимація логарифмічною функцією (з двох розглянутих варіантів).

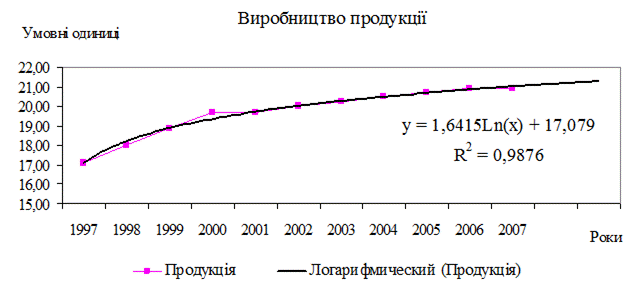
Рисунок 2.22 - Експериментальні дані з апроксимацією логарифмічною кривою

Контрольні запитання і завдання

1. Визначте призначення, методику заповнення аргументів, їх тип і кількість, значення, що повертається, для статистичної функції СчетЕсли.

2. Запишіть формулу обчислення в Excel наступного виразу:
y = (2*x⁵+cos(z)-x*25%)/ 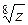, при відомих адресах для х B4 і для z G4

3. Визначте принцип вкладення функцій: кроки майстра, технологію заповнення аргументів на прикладі категорії «статистичні функції» (для 2-х будь-яких вивчених функцій даної категорії).

4. Визначте призначення, аргументи і синтаксис сумісного використання функцій „ЕСЛИ” і „И”, наведіть приклади.

5. Визначте призначення, аргументи і синтаксис функції «ИЛИ», значення, що повертається функцією і його тип, а також напишіть таблицю істинності функції «ИЛИ» для 4-х аргументів.

6. Визначте призначення, аргументи і синтаксис функції «И», значення, що повертається функцією і його тип, а також напишіть таблицю істинності функції «И» для 4-х аргументів.

7. Визначте аргументи функції “ЕСЛИ”, а також значення, що повертається, і його тип. Розберіть приклад реалізації наступної умови: хай необхідно на підставі віку абонента мережі (адреса чарунки Q10) і його доходу (адреса чарунки P10) запропонувати йому або економ-пакет, або стандарт-пакет послуг.

8. Розберіть приклад реалізації в Excel наступної умови: необхідно, якщо клієнт має накопичувальний дисконт (адреса чарунки D7), обчислити нову суму накопичувального дисконту на картці клієнта, збільшену на суму замовлення. Якщо дисконту немає, але сума замовлення клієнта > 500 (адреса чарунки G7), присвоїти замовленню клієнта 3 % знижку. Зобразіть блок-схему.

9. Опишіть кроки майстра побудови діаграм, а також особливості виділення початкового діапазону рядів даних для графічного аналізу, які необхідно враховувати при побудові діаграм різного типу.

10. Поясніть методику прогнозування шляхом побудови апроксимуючої кривої (лінії тренда), аргументуйте, які з кривих можна застосовувати для апроксимації при вихідному виді експериментальної кривої у = f(x) – крива, що має 3 екстремуми.

11. Поясніть принцип призначення періодів прогнозу і місце розташування прогнозних значень в площині координат діаграми при прогнозуванні в MS Excel за допомогою ліній тренда.

12. Визначте призначення, діапазон зміни і критичні значення коефіцієнта R² при прогнозуванні в MS Excel за допомогою ліній тренда.

13. Перерахуйте види апроксимуючих кривих (стисло), аргументуйте, які з кривих можна застосовувати для апроксимації при вихідному виді експериментальної кривої у = f(x) – монотонно зростаюча крива.

РОЗДІЛ 3

СТВОРЕННЯ ТА АНАЛІЗ ДАНИХ В СУЧАСНИХ СУБД

Дата добавления: 2015-05-24