Определение достоверности различий по t-критерию Стьюдента

Способы вычисления достоверности различий между двумя независимыми результатами

В большинстве случаев в исследованиях студентов, выполняю-их дипломные работы, могут решаться задачи выявления эф-ективности той или иной методики обучения и тренировки с рименением определенных средств, приемов и способов орга-изации занятий. Эти задачи обычно решаются путем проведения равнительного педагогического эксперимента с выделением эк-периментальных и контрольных групп, результаты которых в те­рпи статистики принято называть независимыми [3, 4, 6]. В слу-

Железняк

чае, когда мы имеем дело с результатами, полученными в нача­ле и в конце или на разных этапах проведения эксперимента в одной и той же группе (например, при проведении абсолютного эксперимента), эти результаты считаются зависимыми. Однако здесь мы ограничимся рассмотрением методики обработки толь­ко независимых результатов. В подобных случаях исследователю прежде всего необходимо ответить на вопрос: оказалась ли эф­фективной применяемая экспериментальная методика? С этой целью рассчитывается достоверность различий между получен­ными в итоге проведения сравнительного педагогического экс­перимента результатами экспериментальных и контрольных групп. В педагогических исследованиях различия считаются достовер­ными при 5%-ном уровне значимости, т. е. при утверждении того или иного положения допускается ошибка не более чем в 5 слу­чаях из 100.

/-Критерий Стьюдента относится к параметрическим, следо­вательно, его использование возможно только в том случае, ког­да результаты эксперимента представлены в виде измерений по двум последним шкалам — интервальной и отношений [5, 6, 7]. Проиллюстрируем возможности критерия Стьюдента на конкрет­ном примере.

Предположим, вам необходимо выяснить эффективность обу­чения стрельбе по определенной методике. С этой целью прово­дится сравнительный педагогический эксперимент, где одна группа (экспериментальная), состоящая из 8 человек, занимается по предлагаемой экспериментальной методике, а другая (контроль­ная) — по традиционной, общепринятой. Рабочая гипотеза зак­лючается в том, что новая, предлагаемая вами методика окажется более эффективной. Итогом эксперимента является контрольная стрельба из пяти выстрелов, по результатам которых (табл. 6) нужно рассчитать достоверность различий и проверить правильность выд­винутой гипотезы.

Таблица 6

Что же необходимо сделать для расчета достоверности разли­чий по /-критерию Стьюдента?

1. Вычислить средние арифметические величины X для каждой
группы в отдельности по следующей формуле:

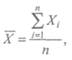
где X_t — значение отдельного измерения; я — общее число изме­рений в группе.

Проставив в формулу фактические значения из табл. 6, получим:

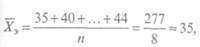
Сопоставление среднеарифметических величин доказывает, что в экспериментально^ группе данная величина (X, = 35) выше, чем в контрольной (Х_к = 27). Однако для окончательного утверж­дения того, что занимающиеся экспериментальной группы на­учились стрелять лучше, следует убедиться в статистической дос­товерности различий (/) между рассчитанными среднеарифмети­ческими значениями.

2. В обеих группах вычислить стандартное отклонение (5) по
следующей формуле:

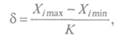
:де X_imax — наибольший показатель; X_imm — наименьший показа­тель; К — табличный коэффициент. Порядок вычисления стандартного отклонения (5): — определить X_itrax в обеих группах; — определить X_imia в этих группах; — определить число измерений в каждой группе (л); — найти по специальной таблице (приложение 12) значение коэффициента К, который соответствует числу измерений в группе (8). Для этого в левом крайнем столбце под индексом (и) находим цифру 0, так как количество измерений в нашем примере меньше 10, а в верхней строке — цифру 8; на пересечении этих строк — 2,85, что соответствует значению коэффициента.АГпри 8 испыту-— подставить полученные значения в формулу и произвести необходимые вычисления:

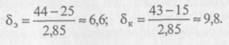
3. Вычислить стандартную ошибку среднего арифметического
значения (т) по формуле:

Для нашего примера подходит первая формула, так как п < 30. Вычислим для каждой группы значения:

4. Вычислить среднюю ошибку разности по формуле:

Дата добавления: 2015-05-08