
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задач
|
|
|
|
Общая схема исследования функции
Ответы к упражнениям
УПРАЖНЕНИЯ
Найти асимптоты:
2.107. y= 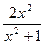 ;
;
2.108. y= 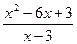 ;
;
2.109. y= 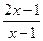 .
.
2.110. y= 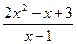 ;
;
2.111. y= 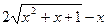 ;
;
2.112. y= 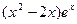 ;
;
2.113. y= 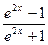 ;
;
2.114. 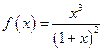 ;
;
2.115. 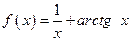 ;
;
2.116. 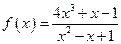 ;
;
2.117. 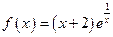 .
.
2.107. y =2 - горизонтальная асимптота; 2.108. x =3 - вертикальная асимптота, y = x -3 – наклонная асимптота; 2.109. x =1 – вертикальная асимптота, y =2 – горизонтальная асимптота; 2.110. x =1 – вертикальная асимптота, y =2 x +1 – наклонная асимптота; 2 .111. y = x +1 и y = -3 x -1 – наклонные асимптоты; 2.112. y = 0 – горизонтальная асимптота; 2.113. y = -1, y =1 – горизонтальные асимптоты. 2.114. х=-1 - вертикальная асимптота; у=х-2 – наклонная асимптота; 2.115. х=0 - вертикальная асимптота; 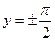 - горизонтальная асимптота; 2.116. y=4x+4 – наклонная асимптота; 2.117. х=0 - вертикальная асимптота; y=x – наклонная асимптота.
- горизонтальная асимптота; 2.116. y=4x+4 – наклонная асимптота; 2.117. х=0 - вертикальная асимптота; y=x – наклонная асимптота.
1. Нахождение области определения.
2. Исследование функции на четность, нечетность и периодичность.
3. Нахождение точек пересечения графика функции с осями координат. Точки пересечения с осью ОХ: (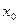 ,0), где
,0), где 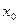 - решение уравнения f(x)= 0. Точки пересечения с осью ОY: (0, f( 0 )).
- решение уравнения f(x)= 0. Точки пересечения с осью ОY: (0, f( 0 )).
4. Нахождение промежутков знакопостоянства функции. Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е. f(x) >0 или f(x) <0.
5. Нахождение производной функции, области определения производной, критических точек.
6. Нахождение промежутков возрастания, убывания, точек экстремума.
7. Нахождение промежутков выпуклости функции и точек перегиба.
1. Исследование поведения функции на бесконечности и в окрестности точек разрыва. Нахождение вертикальных, горизонтальных, наклонных асимптот.
2. Построение графика (при необходимости нужно найти значения функции в дополнительных точках).
ПРИМЕР 1. Исследовать функцию f(x) = 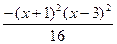 и построить график;
и построить график;
1. D (f) =ℝ  .
.
2. f(-x) 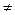 f(x) и f(-x)
f(x) и f(-x) 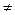 -f(x), следовательно, f(x) - функция общего вида.
-f(x), следовательно, f(x) - функция общего вида.
3. Точки пересечения с осями координат:
OX: y= 0, 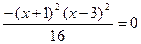 , x = -1, x =3; (-1,0), (3,0);
, x = -1, x =3; (-1,0), (3,0);
OY: x= 0, f( 0 ) = - 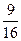 ; (0,-
; (0,- 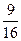 ).
).
4. Промежутки знакопостоянства:
f(x)< 0 при x 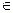 (-
(- 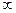 ,-1)
,-1) 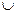 (-1,3)
(-1,3) 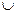 (3,+
(3,+ 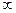 )
)
5. Найдем производную функции, промежутки возрастания, убывания, точки экстремума
Область определения производной функции: D (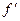 ) = R.
) = R.
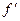 = 0, x= -1, x= 3, x= 1.
= 0, x= -1, x= 3, x= 1.
f(x) возрастает на промежутках (-  ,-1] и [1,3];
,-1] и [1,3];
f(x) убывает на промежутках [-1,1] и [3,+  ).
).
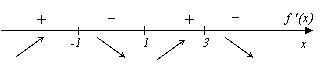
Точки экстремума: 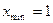 , f( 1 ) = -1;
, f( 1 ) = -1;
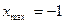 , f( -1 ) = 0;
, f( -1 ) = 0;
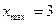 , f( 3 ) = 0;
, f( 3 ) = 0;
6. Найдем промежутки выпуклости, вогнутости функции и ее точки перегиба.
После преобразований получим, что
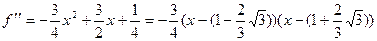 .
.
Обозначим 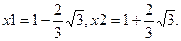
Таким образом, получим
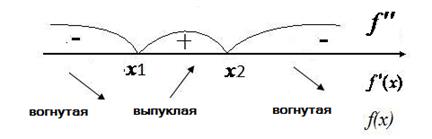
7.
1.Вертикальных асимптот нет, так как f(x) определена(и непрерывна) на всей числовой прямой.
Исследуем поведение функции на бесконечности.
2. Исследуем на наличие горизонтальных асимптот.

 f(x) =
f(x) = 
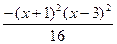 =
= 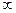 ,
,
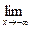 f(x) =
f(x) = 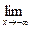
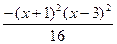 =
= 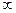 .
.
Таким образом, горизонтальные асимптоты отсутствуют.
3. Исследуем на наличие наклонных асимптот.
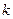 =
= 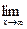
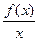 =
= 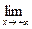
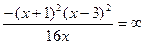 .
.
Таким образом, наклонные асимптоты отсутствуют.
8. Дополнительные точки: f( -3 ) = -9, f( 5 ) = -9.
9. Построим график функции:
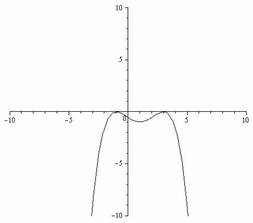
Рис.2.16
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 401; Нарушение авторских прав?; Мы поможем в написании вашей работы!