К каноническому виду методом Лагранжа

Приведение квадратичных форм

Рассмотрим наиболее простой и чаще используемый на практике способ приведения квадратичной формы к каноническому виду, называемый методом Лагранжа. Он основан на выделении полного квадрата в квадратичной форме.

Теорема 10.1 (теорема Лагранжа).Любую квадратичную форму (10.1):

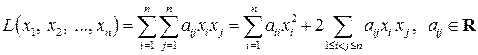
при помощи неособенного линейного преобразования (10.4) можно привести к каноническому виду (10.6):

,

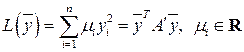где .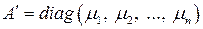

□ Доказательство теоремы проведем конструктивным способом, используя метод Лагранжа выделения полных квадратов. Задача заключается в том, чтобы найти неособенную матрицу 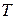такую, чтобы в результате линейного преобразования (10.4) получилась квадратичная форма (10.6) канонического вида. Эта матрица будет получаться постепенно как произведение конечного числа матриц специального типа.

Пункт 1(подготовительный).

1.1. Выделим среди переменных 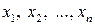такую, которая входит в квадратичную форму в квадрате и в первой степени одновременно (назовем ее ведущей переменной). Перейдем к пункту 2.

1.2. Если в квадратичной форме нет ведущих переменных (при всех : ), то выберем пару переменных, произведение которых входит в форму с отличным от нуля коэффициентом и перейдем к пункту 3.

1.3. Если в квадратичной форме отсутствуют произведения разноименных переменных, то данная квадратичная форма уже представлена в каноническом виде (10.6). Доказательство теоремы завершено.

Пункт 2 (выделение полного квадрата).

2.1. По ведущей переменной выделим полный квадрат. Без ограничения общности предположим, что ведущей переменной является переменная 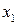. Группируя слагаемые, содержащие 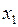, получаем

.

Выделяя полный квадрат по переменной 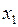в 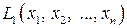, получим

.

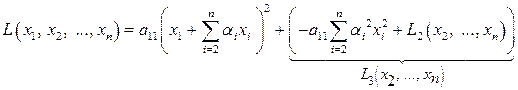Таким образом, в результате выделения полного квадрата при переменной получим сумму квадрата линейной формы

,

в которую входит ведущая переменная , и квадратичной формы от переменных , в которую ведущая переменная уже не входит. Сделаем замену переменных (введем новые переменные )

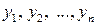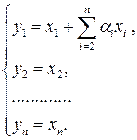
Выразив старые переменные 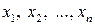через новые :

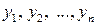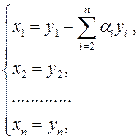
получим матрицу

() неособенного линейного преобразования 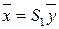, в результате которого квадратичная форма (10.1) примет следующий вид

.

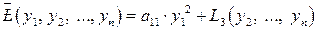С квадратичной формой 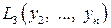поступим также, как и в пункте 1.

2.1. Если ведущей переменной является переменная , то можно поступить двумя способами: либо выделять полный квадрат при этой переменной, либо выполнить переименование (перенумерацию) переменных:

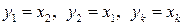
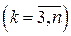
с неособенной матрицей преобразования:

.

Пункт 3 (создание ведущей переменной). Выбранную пару переменных заменим на сумму и разность двух новых переменных, а остальные старые переменные заменим на соответствующие новые переменные. Если, например, в пункте 1 было выделено слагаемое

(, ),

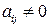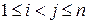то соответствующая замена переменных имеет вид

.

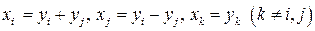При этом

,

и в квадратичной форме (10.1) будет получена ведущая переменная.

Например, в случае замены переменных:

матрица этого неособенного линейного преобразования имеет вид

.

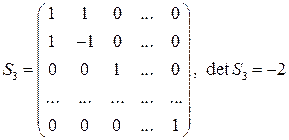В результате приведенного алгоритма (последовательного применения пунктов 1, 2, 3) квадратичная форма (10.1) будет приведена к каноническому виду (10.6).

Заметим, что в результате производимых преобразований над квадратичной формой (выделение полного квадрата, переименование и создание ведущей переменной) мы использовали элементарные неособенные матрицы трех типов (они являются матрицами перехода от базиса к базису). Искомая матрица 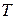неособенного линейного преобразования (10.4), при котором форма (10.1) имеет канонический вид (10.6), получается путем произведения конечного числа элементарных неособенных матриц трех типов. ■

Пример 10.2. Привести квадратичную форму

к каноническому виду методом Лагранжа. Указать соответствующее неособенное линейное преобразование. Выполнить проверку.

Решение. Выберем ведущей переменную 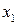(коэффициент ). Группируя слагаемые, содержащие 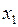, и выделяя по ней полный квадрат, получим

где обозначено

Сделаем замену переменных (введем новые переменные )

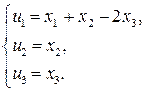
Выразив старые переменные 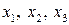через новые :

получим матрицу

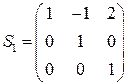
неособенного линейного преобразования , в результате которого исходная квадратичная форма примет вид

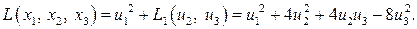
К квадратичной форме 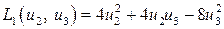применим метод выделения полного квадрата при ведущей переменной :

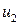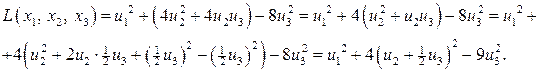
Сделаем снова замену переменной (введем новые переменные )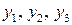

Выразив переменные через новые :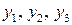

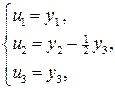
получим матрицу

неособенного линейного преобразования 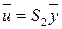, в результате которого квадратичная форма примет искомый канонический вид

Вычислим матрицу 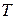неособенного линейного преобразования (10.4). Учитывая равенства

, ,

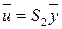получим, что матрица 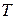имеет вид

.

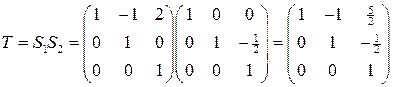Выполним проверку проведённых вычислений. Матрицы исходной квадратичной формы и канонической формы имеют вид

, .

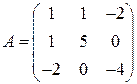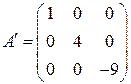Убедимся в справедливости равенства (10.5):

.

Дата добавления: 2015-05-09