Первый закон термодинамики

З-4.5

З-4.4

З-4.3

З-4.2

З-4.1

Задачи

Решение.

П-4.2

Решение.

П-4.1

Примеры

Вычислить среднюю массовую и среднюю объемную теплоемкости окиси углерода при постоянном объеме для интервала температур 0-1200 ºС, если известно, что для окиси углерода
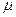( с_рm) ₀¹²⁰⁰=32,192 кДж/(кмоль·К).

Сопоставить полученные результаты с табличными данными.

кДж/(м³·К);

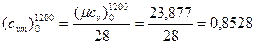кДж/(м³·К);

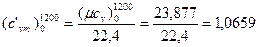кДж/(м³·К).

Из приложения Д

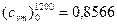кДж/(м³·К);

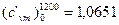кДж/(м³·К).

Воздух в количестве 6 м³ при давлении р₁ = 0,3 МПа и температуре t₁ = 25 ºС нагревается при постоянном давлении до t₂ = 130 ºС.

Определить количество подведенной к воздуху теплоты, считая
с = const.

Для данного случая формула (4.5) примет вид:

.

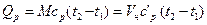Массу газа найдем из уравнения

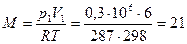кг,

а объем газа при нормальных условиях – из уравнения

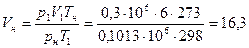нм³.

На основании формул (4.1) имеем

кДж/(кг·К);

кДж/(нм³·К).

Следовательно,

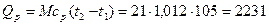кДж,

или

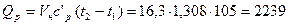кДж.

Баллон с водородом выносится из помещения с температурой 5 ºС в машинный зал, где температура достигает 25 ºС.

Определить количество теплоты, полученной газом после выравнивания температуры, если начальное давление в баллоне составляло 12 МПа. Объем баллона 40 дм³.

Ответ: Q_v = 84 кДж.

Воздух выходит из компрессора при p₁ = 0,7 МПа и t₂ = 160 ºС и поступает в холодильник. На выходе из холодильника температура воздуха равна 25 ºС.

Определить количество теплоты, отданной охлаждающей воде в течение часа, если производительность компрессора V = 6 м³/мин.

Ответ: Q = 275435 кДж/ч.

В регенеративном подогревателе газовой турбины воздух нагревается при постоянном давлении от t₁ =130 ºС до t₂ =500 ºС.

Определить количество теплоты, сообщенной воздуху в единицу времени, если расход его составляет 250 кг/ч. Ответ дать в килоджоулях в секунду и в киловаттах. Для решения воспользоваться таблицами.

Ответ: Q =27 кДж/с=27 кВт.

Используя таблицу 3, найти объемную теплоемкость кислорода при постоянном объеме и постоянном давлении, считая с = const.

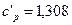Ответ: кДж/(м³·К); кДж/(м³·К).

Определить значение массовой теплоемкости кислорода при постоянном объеме и постоянном давлении, считая с = const.

Ответ: с_p = 0,916 кДж/(кг·К); с_v = 0,654 кДж/(кг·К).

Первый закон термодинамики является частным случаем закона сохранения и превращения энергии. Он устанавливает эквивалентность при взаимных превращениях механической и тепловой энергии и математически может быть выражен следующим образом:

Q = L, (5.1)

где Q – количество теплоты, превращенной в энергии, Дж;

L – работа, полученная за счет теплоты Q, Дж.

Аналитическое выражение первого закона термодинамики или основное уравнение теплоты в дифференциальной форме для любого тела

dQ = dU + dL, (5.2)

где dQ – количество теплоты, сообщенное извне рабочему телу массой М кг;

dU – изменение внутренней энергии рабочего тела;

dL – работа, совершенная рабочим телом по преодолению внешнего давления.

Каждый из трех членов этого уравнения может быть в зависимости от характера изменения состояния положительным, отрицательным или равным нулю. Для бесконечно малого изменения состояния
1 кг любого газа уравнение (5.2) примет вид:

dq = du + dl. (5.3)

Так как

dа = pdv,

то

dq = du + pdv. (5.4)

Для конечного изменения состояния уравнения (5.2) и (5.3) примут вид

Q = ΔU + L, (5.5)

q = Δu + l. (5.6)

Работа расширения 1 кг газа

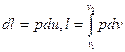, (5.7)

Изменение внутренней энергии идеального газа для любого процесса при бесконечно малом изменении состояния (для 1кг)

du = c_vdt. (5.8)

В теплотехнических расчетах обычно требуется знать изменение внутренней энергии Δu, а не ее абсолютное значение. Интегрируя уравнение (5.8) в пределах от t₁ до t₂, получаем

Δu = c_vm(t₂ - t₁), (5.9)

где c_vm – средняя массовая теплоемкость при постоянном объеме в пределах от t₁ до t₂.

Заменяя в уравнении (5.4) величину pdv через (d(pv) – vdp) получаем

dq = du + d(pv) – vdp = d(u + pv) – vdp.

Выражение u + pv является параметром состояния. В технической термодинамике этот параметр называется энтальпия и обозначается буквой i. Таким образом

i = u + pv, (5.10)

следовательно, основное уравнение первого закона термодинамики, выраженное через энтальпию, имеет вид

dq = di – vdp. (5.11)

Так как для идеальных газов di = c_d ·dT, то

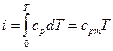, (5.12)

где c_рm – средняя массовая теплоемкость при постоянном давлении в пределах от 0º до Т.

В теплотехнических расчетах обычно требуется знать изменение энтальпии, а не ее абсолютное значение. Интегрируя уравнение (5.11) при p = const, получаем

q_p = i₂ – i₁. (5.13)

Дата добавления: 2015-05-09