Аналитическое выражение первого начала термодинамики

Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом:

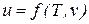; (53)

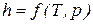. (54)

Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями

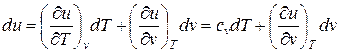; (55)

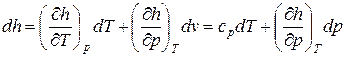. (56)

Соотношения (55) и (56) получены, исходя из анализа зависимостей (19), (48), который показывает, что для изохорного процесса (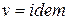) частная производная внутренней энергии по температуре равна истинной изохорной теплоемкости

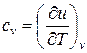, (57)

а для изобарного процесса (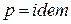) частная производная энтальпии по температуре равна истинной изобарной теплоемкости

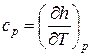. (58)

В результате подстановки выражений (55) и (56) в уравнение (48) и разделения переменных получим:

. (59)

Данное соотношение (59) называется первым началом термодинамики для простых тел в аналитической форме.

Выражения в квадратных скобках уравнения (59) в литературе часто называют калорическими коэффициентами, которые могут быть определены по формулам, полученным с использованием дифференциальных соотношений термодинамики,

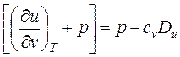, (60)

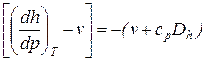, (61)

где 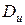– коэффициент Джоуля – Гей Люссака,

; (62)

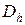– коэффициент Джоуля-Томсона,

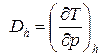. (63)

Коэффициенты Джоуля – Гей Люссака (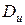) и Джоуля-Томсона (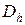) реальных газов определяются по таблицам термодинамических свойств, представленным в справочной литературе.

Дата добавления: 2015-05-09