
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод термодинамических потенциалов
|
|
|
|
Цель метода – выразить производные таким образом, чтобы их можно было вычислить, используя уравнения состояния.
Задачи:
1) Доказать соотношения Гиббса-Гельмгольца.
Решение: Приравнивая, друг другу вторые производные термодинамических потенциалов, получим:
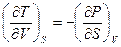 ;
; 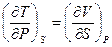 ;
; 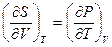 ;
; 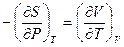 ;
;
E W F Φ
2) Доказать, что 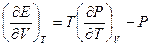 и
и 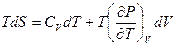 . Используя связь между давлением и плотностью энергии черного излучения
. Используя связь между давлением и плотностью энергии черного излучения 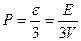 , получить закон Стефана – Больцмана.
, получить закон Стефана – Больцмана.
Решение: Используя первое начало термодинамики:
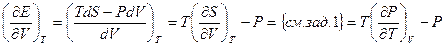 .
.
 Для идеального газа
Для идеального газа 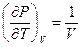 и, следовательно
и, следовательно 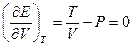 . Для ван-дер-ваальсовского газа
. Для ван-дер-ваальсовского газа 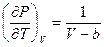 и
и 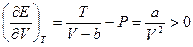 . Таким образом, энергия ван-дер-ваальсовского газа при расширении увеличивается. Подавляется
. Таким образом, энергия ван-дер-ваальсовского газа при расширении увеличивается. Подавляется 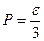 ,
, 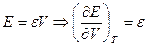 в полученное уравнение, находим:
в полученное уравнение, находим:
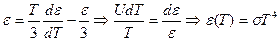 .
.
Пусть 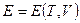 . Тогда
. Тогда 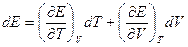 = {из полученного соотношения} =
= {из полученного соотношения} = 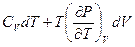 .
.
3) Доказать указанные термодинамические равенства (на основании первого начала термодинамики и задачи 1).
a. 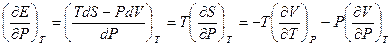
b. 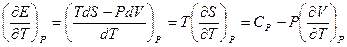
c. 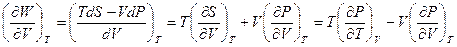
d. 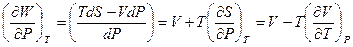
e. 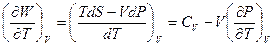 .
.
4) Найти для одного моля 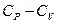 .
.
Решение: 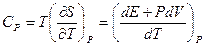 ={из задачи 2}=
={из задачи 2}= 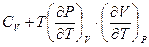 .
.
Для идеального газа 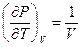 ;
; 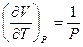 . Следовательно,
. Следовательно, 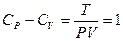 -уравнение Майера. Для ван-дер-ваальсовского газа чтобы найти
-уравнение Майера. Для ван-дер-ваальсовского газа чтобы найти 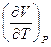 , выразим
, выразим 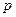 из уравнения состояния и продифференцируем полученное равенство:
из уравнения состояния и продифференцируем полученное равенство:
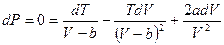 ,
,
откуда
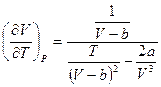 =
= 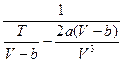 =
= 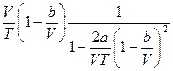 .
.
Так как 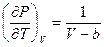 , то
, то 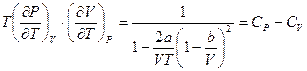 .
.
В первом приближении по малым параметрам 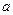 и
и 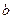
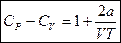 .
.
5) Найти уравнение адиабаты.
Решение: 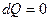 , и как следует из задачи 2.
, и как следует из задачи 2. 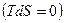 :
:
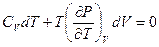 (1).
(1).
a. Идеальный газ 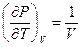 . Подставляя в (1) и разделяя переменные, получаем:
. Подставляя в (1) и разделяя переменные, получаем: 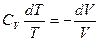 . Следовательно,
. Следовательно, 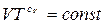 или, с учетом того, что
или, с учетом того, что 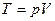
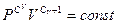 , или
, или 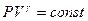 (
(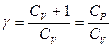 ).
).
b. Ван-дер-ваальсовский газ 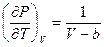 . Из (1) получаем
. Из (1) получаем 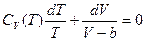 Þ
Þ 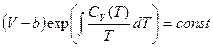 .
.
6) Найти уравнение политропы 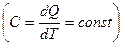 .
.
Решение: Воспользуемся результатом задач 2 и 3г:
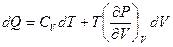 ,
, 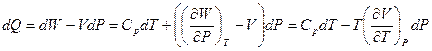 . Следовательно
. Следовательно 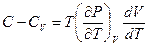 , и
, и 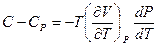 . Разделим одно из уравнений на другое:
. Разделим одно из уравнений на другое:
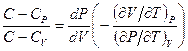 =
= 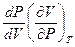 .
.
Для идеального газа 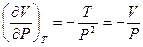 , и уравнение принимает вид:
, и уравнение принимает вид:
χ= 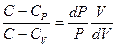 или
или 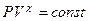 .
.
7) Найти 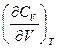 и
и 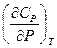 .
.
Решение:
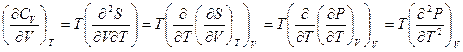 ;
; 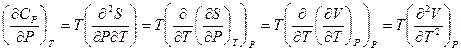 .
.
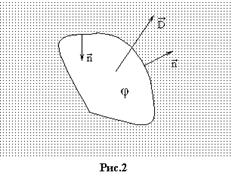
8) Найти работу поляризации единицы объема диэлектрика.
Решение: Выберем модель – бесконечный диэлектрик, поле в котором создается проводником с зарядом 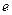 потенциалом
потенциалом 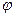 (на поверхности
(на поверхности 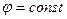 , а на бесконечности
, а на бесконечности 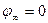 ). Внесем заряд
). Внесем заряд 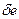 из бесконечности на поверхность проводника. При этом придется совершить работу против сил электрического поля. Эта работа пойдет на поляризацию и увеличение энергии электрического поля. По определению
из бесконечности на поверхность проводника. При этом придется совершить работу против сил электрического поля. Эта работа пойдет на поляризацию и увеличение энергии электрического поля. По определению 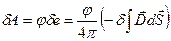 = {за счет того, что нормаль внешняя к диэлектрику} =(
= {за счет того, что нормаль внешняя к диэлектрику} =(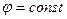 )=
)= 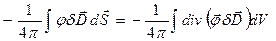 = =
= = 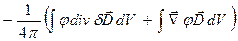 = {т.к. в объеме нет сторонних зарядов
= {т.к. в объеме нет сторонних зарядов 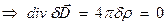 }=
}= 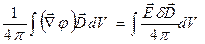 .
.
Работа над единицей объема равна 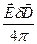 и складывается (
и складывается (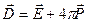 ) из работы по изменению электрического поля внутри диэлектрика
) из работы по изменению электрического поля внутри диэлектрика 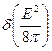 и работы поляризации
и работы поляризации 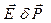 .
.
NB 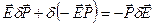 - работа внешнего источника при изменении поля на
- работа внешнего источника при изменении поля на 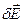 .
.
9) Работа по намагничиванию единицы объема магнетика.
Решение: Само магнитное поле работы над зарядами не совершает, но индуцируемое переменным магнитным полем вихревое электрическое поле способно совершать работу. Обратно, работа, взятая с обратным знаком, есть работа, которую совершает внешняя сила, поддерживающая протекание токов, по созданию электромагнитного поля. Закон сохранения энергии для электронов имеет вид 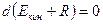 .
.
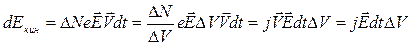 , следовательно:
, следовательно:
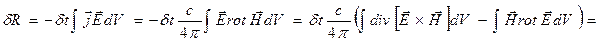
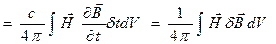 .
.
Эта работа складывается из (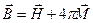 ) работы по увеличению энергии магнитного поля
) работы по увеличению энергии магнитного поля 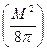 и работы по намагничиванию единицы объема
и работы по намагничиванию единицы объема 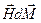 . Если к последней добавить изменение потенциальной энергии единицы объема магнетика
. Если к последней добавить изменение потенциальной энергии единицы объема магнетика 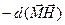 , то получим
, то получим 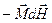 - работу внешнего поля при его изменении на
- работу внешнего поля при его изменении на 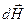 над магнетиком
над магнетиком 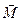 .
.
10) Найти работу упругих сил.
Решение: Выберем в качестве модели неограниченно упругую среду, вектор деформации которой 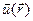 . Определим бесконечно малую работу, которую необходимо затратить на создание поля
. Определим бесконечно малую работу, которую необходимо затратить на создание поля 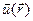 . Эта работа производится внешним источником сил против сил внутренних напряжений. Следовательно, работа сил внутренних напряжений будет с обратным знаком. Сила внутренних напряжений
. Эта работа производится внешним источником сил против сил внутренних напряжений. Следовательно, работа сил внутренних напряжений будет с обратным знаком. Сила внутренних напряжений 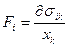 , где
, где 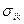 - тензор напряжений (на бесконечности компоненты тензора обнуляются).
- тензор напряжений (на бесконечности компоненты тензора обнуляются).
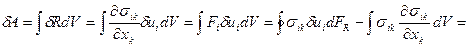
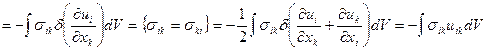 ,
,
где 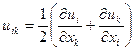 - тензор деформаций.
- тензор деформаций.
Следовательно, работа упругих сил над единицей объема 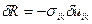 .
.
11) Доказать, что если из трех переменных A,B,C являются дифференцируемой функцией двух других переменных, то выполняются соотношения:
1. 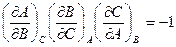
2. 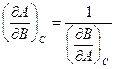
На основании этих равенств установим связь между термическими коэффициентами:
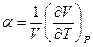 - коэффициент температурного расширения.
- коэффициент температурного расширения.
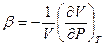 - коэффициент изотермического сжатия.
- коэффициент изотермического сжатия.
 - коэффициент термического давления.
- коэффициент термического давления.
Решение: Рассмотрим поверхность 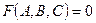 и три ее сечения плоскостями
и три ее сечения плоскостями 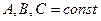 . Для точек поверхности:
. Для точек поверхности:
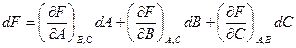 .
.
В сечениях получаются плоские кривые:
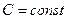 Þ
Þ 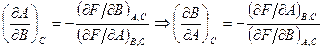
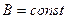 Þ
Þ 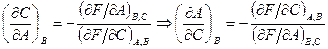
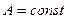 Þ
Þ 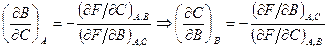
Перемножая эти равенства, получаем условие задачи. Если 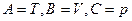 то нетрудно получить искомое соотношение
то нетрудно получить искомое соотношение 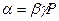 .
.
12) Показать, что 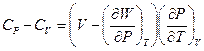 .
.
Решение: Как следует из результата задачи 4: 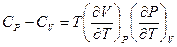 , так как (см. 3г)
, так как (см. 3г) 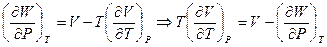 , то получаем требуемое условие.
, то получаем требуемое условие.
Метод функциональных определителей (якобианов)
Рассмотрим две функции двух переменных: 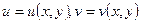
Определитель
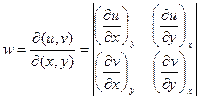 - называется якобианом,
- называется якобианом,
так что 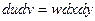 .
.
Свойства якобиана следуют из его определения:
1) При 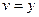
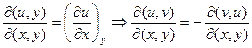 ;
;
2) 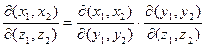 , т.е. с якобианами можно формально обращаться как с дробями.
, т.е. с якобианами можно формально обращаться как с дробями.
3) 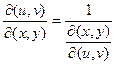
Задачи:
13. Найти 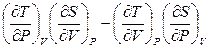 .
.
Решение:
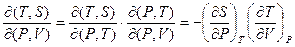 = (из соотношений Максвелла)=
= (из соотношений Максвелла)= 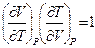 .
.
14. Найти 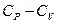 методом якобианов.
методом якобианов.
Решение:
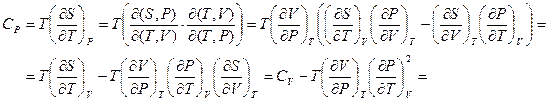
(из соотношений Максвелла)= 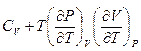 .
.
15. Доказать, что 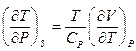 .
.
Решение:
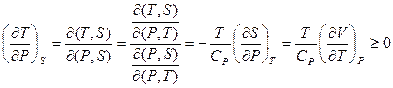 (из соотношений Максвелла).
(из соотношений Максвелла).
16. Доказать, что 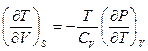 .
.
Решение:
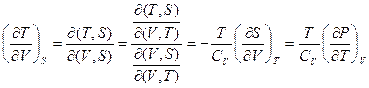 .
.
17. Доказать, что 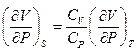 .
.
Решение:
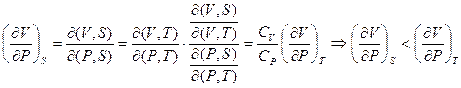 .
.
18. Доказать, что 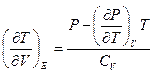 .
.
Решение:
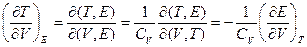 = (См. задачу 2.) =
= (См. задачу 2.) = 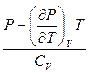 .
.
19. Термодинамическая система расширяется так, что ее энергия постоянна. Как изменяется ее температура? Будет ли такой процесс адиабатным?
Решение: Необходимо найти производную 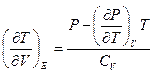 . Для идеального газа
. Для идеального газа 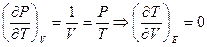 . Для ван-дер-ваальсовского газа:
. Для ван-дер-ваальсовского газа:
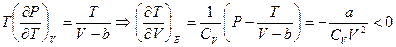
(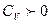 , следовательно, газ охлаждается.). Чтобы ответить на второй вопрос, необходимо найти производную:
, следовательно, газ охлаждается.). Чтобы ответить на второй вопрос, необходимо найти производную:
 (при
(при 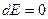 из первого начала термодинамики находим
из первого начала термодинамики находим 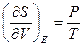 )=
)= 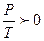 . Так как
. Так как 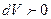 , следовательно
, следовательно 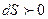 , т.е. процесс необратим.
, т.е. процесс необратим.
20. Для единицы объема диэлектрика найти 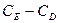 .
.
Решение: 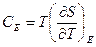 ,
, 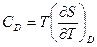 . (
. (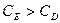 , так как при постоянном
, так как при постоянном  внешний источник тепла должен затратить дополнительную работу
внешний источник тепла должен затратить дополнительную работу  по поляризации.)
по поляризации.) 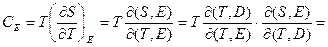 (
(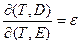 -диэлектрическая проницаемость)=
-диэлектрическая проницаемость)= 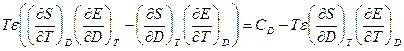 .
.
Производную 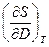 найдем из выражения для плотности свободной энергии
найдем из выражения для плотности свободной энергии 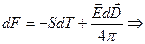
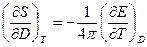 .
.
Таким образом
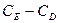 =
= 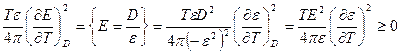 .
.
NB Эта формула определяют изменение теплоемкости вещества конденсатора при отключении его от источника питания ( ).
).
21. Найти работу, совершаемую газом при квазистатическом адиабатическом переходе.
Решение: По условию 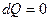 , т.е.
, т.е. 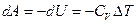 , т.е. газ совершает работу за счет запасов внутренней энергии.
, т.е. газ совершает работу за счет запасов внутренней энергии.
22. 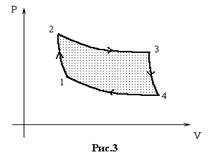 Доказать, что для цикла Карно уравнение Клаузиуса
Доказать, что для цикла Карно уравнение Клаузиуса 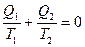 , где Q1, T1 – количество тепла и температура нагревателя; Q2, T2 – холодильника.
, где Q1, T1 – количество тепла и температура нагревателя; Q2, T2 – холодильника.
Решение: Цикл Карно – один из примеров получения полезной работы (см. ниже) от неравновесной системы (нагреватель - холодильник). Для этого необходимо рабочее тело. Участки 2-3 и 4-1 – изотермы (соответствующие температурам 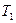 и
и 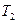 ,
, 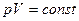 ).Участки 3-4 и 1-2 – адиабаты (
).Участки 3-4 и 1-2 – адиабаты (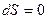 ), следовательно
), следовательно 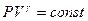 (рис.3). Так как рабочее тело возвращается в исходное состояние, то для всего процесса
(рис.3). Так как рабочее тело возвращается в исходное состояние, то для всего процесса 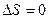 . С другой стороны:
. С другой стороны: 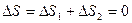 , так как на участке 2–3
, так как на участке 2–3 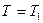 , а на
, а на 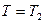 , то
, то 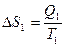 ,
, 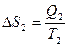 откуда и следует утверждение задачи.
откуда и следует утверждение задачи.
23. Доказать, что пересечение двух адиабат невозможно, так как это приводит к нарушению принципа Томсона.
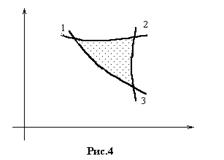 Решение: Надо напомнить содержание этого принципа. Он гласит, что невозможен круговой процесс, при котором все тепло переходит в работу. Если
Решение: Надо напомнить содержание этого принципа. Он гласит, что невозможен круговой процесс, при котором все тепло переходит в работу. Если 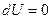 следовательно на этом участке
следовательно на этом участке 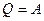 . Однако, необходимо вернуть рабочее тело в исходное состояние. Для этого необходим холодильник. Если бы после расширения все молекулы газа сами по себе заняли исходный объем, то такой процесс был бы возможен. Итак, предположим противное, т.е., что адиабаты пересекаются. Соединив их изотермой, получим круговой процесс (23).
. Однако, необходимо вернуть рабочее тело в исходное состояние. Для этого необходим холодильник. Если бы после расширения все молекулы газа сами по себе заняли исходный объем, то такой процесс был бы возможен. Итак, предположим противное, т.е., что адиабаты пересекаются. Соединив их изотермой, получим круговой процесс (23).
1-2 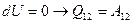
2-3 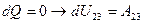
3-1: 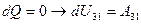
Суммарная работа 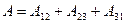 , но т.к. тело возвращается в исходное состояние, то
, но т.к. тело возвращается в исходное состояние, то 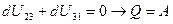 , т.е. все тепло перешло в работу. Мы получили противоречие.
, т.е. все тепло перешло в работу. Мы получили противоречие.
24. Вывести выражение для энтропии, в случае, когда 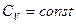 .
.
Решение: Из первого начала получаем:
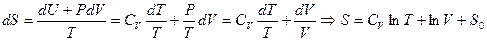 .
.
При расширении в вакуум идеального газа 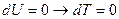 и
и 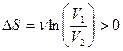 . Следовательно, процесс необратим.
. Следовательно, процесс необратим.
25. Доказать, что в процессе при постоянном давлении возрастание энтропии в γ раз больше, чем в процессе при постоянном объеме.
Решение:
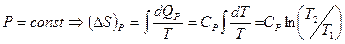
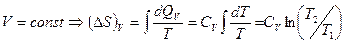
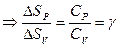
26. Получить выражение для коэффициентов теплового расширения ван-дер-ваальсовского газа.
Решение: В задаче 4 было получено выражение:

в первом приближении (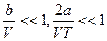 )
)
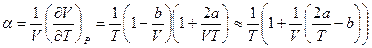 .
.
27. Установить критерии термодинамического и механического равновесия.
Решение: В состоянии термодинамического равновесия энтропия максимальна. Рассмотрим две части замкнутой системы. Суммарная энтропия в состоянии равновесия максимальна (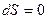 ). Так как
). Так как 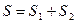 , то
, то 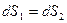 . Следовательно:
. Следовательно:
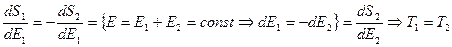
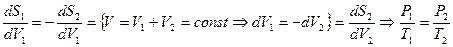 ;
;
(если система замкнута и 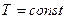 , то
, то 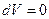 , если
, если 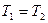 то
то 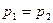 . Здесь использовано первое начало термодинамики в виде
. Здесь использовано первое начало термодинамики в виде 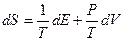 .
.
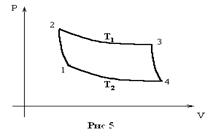
28. Найти плотность энтропии поля излучения, если 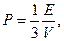
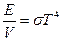 . Изобразить изотермы и адиабаты для цикла Карно такого газа.
. Изобразить изотермы и адиабаты для цикла Карно такого газа.
Решение: Используем первое начало термодинамики:
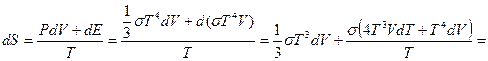
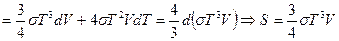 .
.
 Следовательно, плотность энергии
Следовательно, плотность энергии 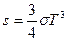 . Так как
. Так как 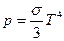 то изотермы и изобары для такой системы– суть одно и тоже. Адиабата такого газа определяется уравнением
то изотермы и изобары для такой системы– суть одно и тоже. Адиабата такого газа определяется уравнением 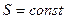 или
или 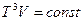 . В переменных
. В переменных 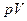 (
(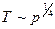 )
) 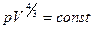 .
.
1-2, 3-4 на рисунке – изотермы, а 2-3, 4-1 – адиабаты.
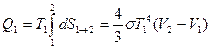
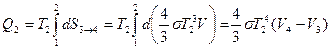
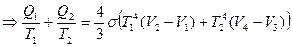
Но для участков 2-3, 1-4 (адиабат) 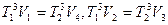 Поэтому для фотонного газа выполняется уравнение Клаузиуса:
Поэтому для фотонного газа выполняется уравнение Клаузиуса: 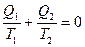 .
.
29. Два одинаковых идеальных газа с одинаковыми температурами и числом частиц, но разными давлениями 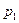 и
и 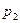 , находятся в двух сосудах. Сосуды соединяются. Найти изменение энтропии.
, находятся в двух сосудах. Сосуды соединяются. Найти изменение энтропии.
Решение: Так как температуры систем одинаковы, то 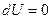 (так как кинетическая энергия молекул и следовательно температура не изменяются). Поэтому
(так как кинетическая энергия молекул и следовательно температура не изменяются). Поэтому
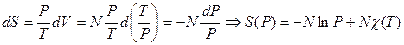
До соединения 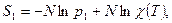
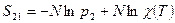 , а после
, а после  .
.
Установившееся давление определяется из соотношения:
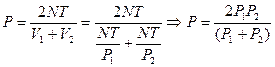
Таким образом, изменение энтропии
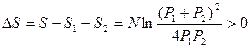
30. Две колбы наполнены одинаковым идеальным газом, находящимся при одном давлении, но с разными температурами 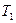 и
и 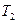 . Сосуды соединяются. Найти изменение энтропии (число частиц в колбах одинаково).
. Сосуды соединяются. Найти изменение энтропии (число частиц в колбах одинаково).
Решение: Используем общую формулу(R = 1):
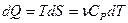 (для процесса при постоянном давлении),
(для процесса при постоянном давлении), 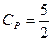 . Поэтому для начальных и конечных состояний (
. Поэтому для начальных и конечных состояний (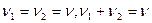 ).
).
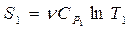
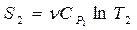
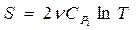 .
.
Конечную температуру 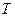 определим из соотношения:
определим из соотношения:
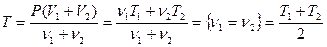
Поэтому 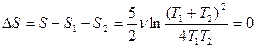 (если
(если 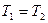 ).
).
31. Определить скорость звуковой волны распространяющейся в ван-дер-ваальсовском газе.
Решение: Рассмотрим один моль вещества (ван-дер-ваальсовский газ) (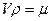 ). Согласно механике сплошных сред:
). Согласно механике сплошных сред:
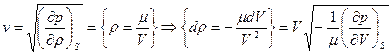
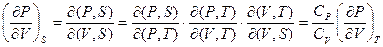
Следовательно
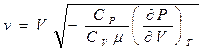 .
.
Для ван-дер-ваальсовского газа 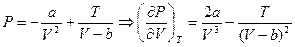 .
.
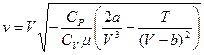 = (в первом приближении
= (в первом приближении 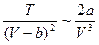 ) =
) = 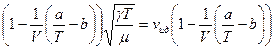 (
(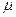 – масса одного моля газа).
– масса одного моля газа).
32. Найти изменение температуры с высотой, используя адиабатичность расширения восходящих потоков воздуха.
Решение: (В этой задаче будем пользоваться уравнением Менделеева - Клайперона в общем виде: 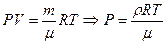 ).
).
Изменение давления с высотой определяется формулой: 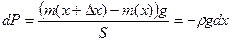
(так как на верхний слой давит меньший столб воздуха, чем на нижний).
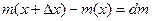 - масса столбика высотой
- масса столбика высотой 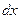 .
.
Уравнение адиабаты 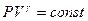 можно переписать в виде:
можно переписать в виде: 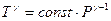 ,
, 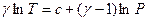 или
или 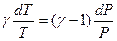 . Подставляя
. Подставляя 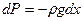 ,
, 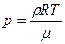 получим сразу:
получим сразу:
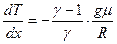 .
.
Для воздуха 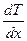 = 10
= 10 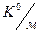 .
.
32. Определить температуру кромки крыла самолета, движущегося со скоростью 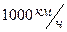 . Температура окружающего воздуха
. Температура окружающего воздуха 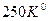 .
.
Решение: Уравнение непрерывности сводится к 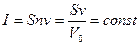 (поток постоянен в каждом сечении).
(поток постоянен в каждом сечении).
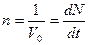 (
(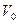 – объем, приходящийся на одну частицу) – концентрация. За время
– объем, приходящийся на одну частицу) – концентрация. За время 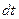 изменяются:
изменяются:
- Кинетическая энергия
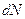 частиц связанная с их поступательным движением по трубке
частиц связанная с их поступательным движением по трубке 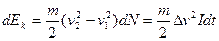 .
. -
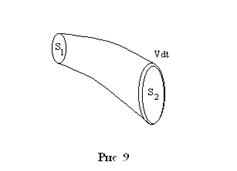 Внутренняя энергия (кинетическая энергия хаотичного движения)
Внутренняя энергия (кинетическая энергия хаотичного движения)
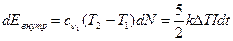 (для двухатомного газа).
(для двухатомного газа).
- Совершается работа
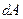 над этими же
над этими же 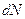 частицами за время
частицами за время 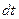 :
:
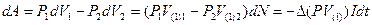
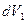 – объем, занимаемый
– объем, занимаемый 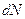 – частицами вблизи сечения 1. Из первого начала термодинамики в расчете на одну частицу:
– частицами вблизи сечения 1. Из первого начала термодинамики в расчете на одну частицу:
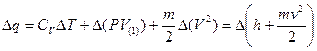
здесь 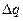 – количество тепла, полученное частицей при движении от сечения 1 к 2,
– количество тепла, полученное частицей при движении от сечения 1 к 2, 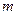 – масса одной молекулы,
– масса одной молекулы, 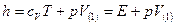 – удельная энтальпия.
– удельная энтальпия.
Используя уравнения Менделеева – Клайперона 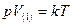 и Майера
и Майера 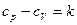 запишем выражение для удельных внутренней энергии и энтальпии:
запишем выражение для удельных внутренней энергии и энтальпии:
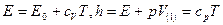
Так как течение адиабатическое, то (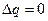 )
)
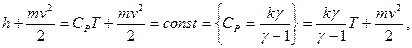
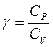
Из этого уравнения получим (сравнивая эту величину на бесконечности и вблизи, где 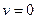 ):
):
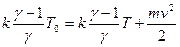 ,
,
но 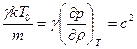 - скорость звука. Следовательно:
- скорость звука. Следовательно:
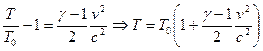 .
.
С учетом условий задачи:
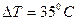 и
и 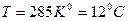 .
.
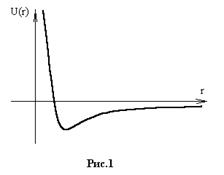
33. Рассмотреть эффект Джоуля – Томсона.
Решение: на эффекте Джоуля – Томсона построен один из методов охлаждения газов (позволяет получать температуры до  ). Сам процесс заключается в продавливании газа через полупроницаемую перегородку (дроссель). Пусть изначально газ находился при давлении
). Сам процесс заключается в продавливании газа через полупроницаемую перегородку (дроссель). Пусть изначально газ находился при давлении 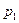 и занимал объем
и занимал объем 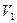 , а после –
, а после – 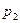 (
(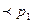 ) и
) и 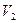 . Работа газа
. Работа газа 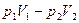 ввиду теплоизолированности системы есть изменение его внутренней энергии (
ввиду теплоизолированности системы есть изменение его внутренней энергии (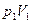 – работа по вытеснению газа из объема
– работа по вытеснению газа из объема 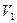 ,
, 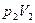 – работа газа по занятию объема
– работа газа по занятию объема 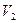 ):
):
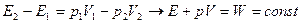
Вычислим производную:
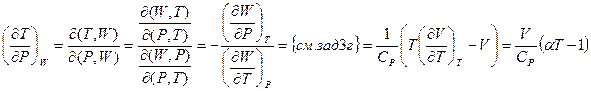
где 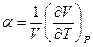 - коэффициент теплового расширения. Для ван-дер-ваальсовского газа (см. задачу 4) в первом приближении:
- коэффициент теплового расширения. Для ван-дер-ваальсовского газа (см. задачу 4) в первом приближении:
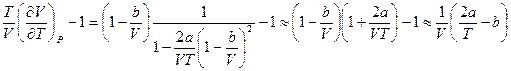
 таким образом
таким образом
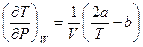 .
.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 3005; Нарушение авторских прав?; Мы поможем в написании вашей работы!