Обе эти величины могут быть измерены экспериментально

Если то газ охлаждается (), если наоборот – нагревается. Если - то эффект отсутствует. Совместно с уравнениями и в переменных это дает так называемую кривую инверсии. Для идеального газа такой эффект отсутствует.

34. Получить абсолютную шкалу температур.

Решение: Необходимо поставить в соответствие друг другу две температурные шкалы 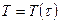, где 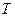– абсолютная шкала, а 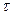– произвольная.

.

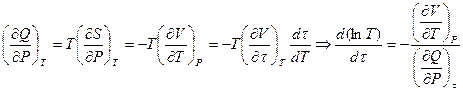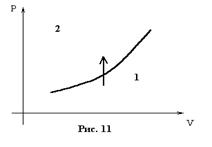
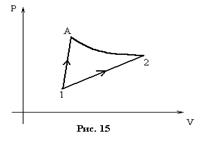
35. Исследовать магнитокалорический эффект.

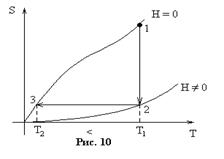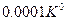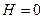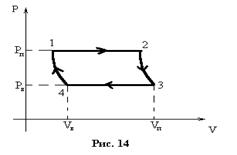
Решение: Магнитоколарический эффект применяется для получения сверхнизких температур (до ) парамагнитных солей. Идея заключается в том, что при энтропия системы больше, чем при 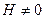. Участок 1-2 на рисунке описывает изотермическое включение поля, а участок 2-3 – адиабатическое выключение. Запишем первое начало термодинамики с учетом работы магнитного поля ():

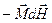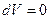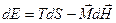(1)

Если внутренняя энергия ,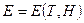

то

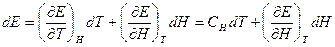(2)

.

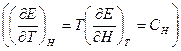Подставляя (2) в (1) и выражая 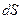, получаем:

.

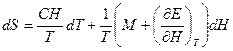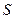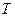Приравнивая друг к другу вторые производные от по и 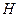, находим:

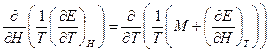
или

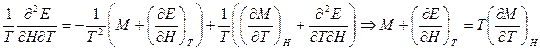
Следовательно

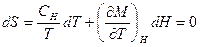(при адиабатическом выключении).

Таким образом

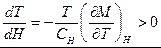(так как 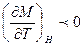). То есть при уменьшении 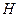уменьшается .

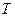35. Получить .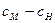

Решение: Как следует из предыдущей задачи:

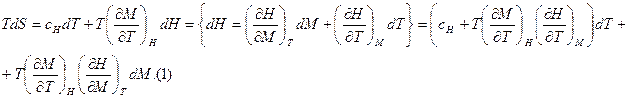
Если 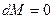, то из (1)следует, что

.

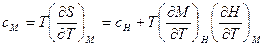Таким образом:

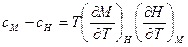
Системы с переменным числом частиц.

Рассмотрим две фазы какого-либо вещества и укажем критерии равновесия фаз (предполагается, что при этом состояния термодинамического и механического равновесия уже достигнуты, т.е. 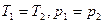). В силу аддитивност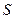и и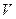

.

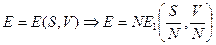
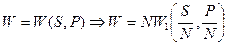
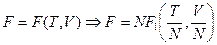
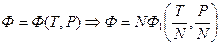(индекс 1 означает термодинамический потенциал одной молекулы).

Учтем зависимость от 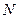термодинамических параметров слагаемым .

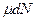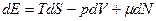
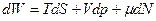
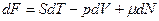
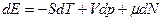
откуда

,

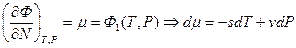(где 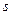и 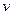- удельные энтропия и объем)

и .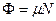

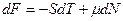(объем выделен 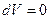, но число частиц в нем меняется). Следовательно:

,

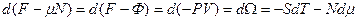где 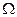- омега-потенциал.

Если для двух фаз давления и температуры совпадают, то энтропия максимальна (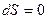). Тогда в силу того, что

:

. (*)

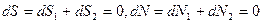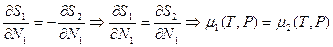Кривая (*) на фазовой диаграмме называется кривой равновесия фаз. Следовательно, критерий равновесия фаз – равенство их химических потенциалов. Чтобы получить уравнение этой кривой на диаграмме 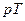, продифференцируем (*):

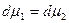
или с учетом выражения для :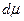

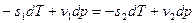
откуда следует уравнение:

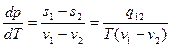, определяющее кривую равновесия фаз (уравнение Клайперона - Клаузиуса).

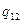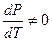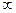Здесь – количество теплоты, в расчете на одну молекулу. Так как или , то 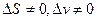. Это значит, что первые производные ( 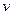и 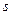) при переходе через кривую (т.н. фазовом переходе) претерпевают скачок. Такой переход называется фазовым переходом первого рода.

36. При каком давлении вода будет кипеть при .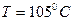

Решение:

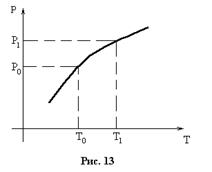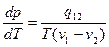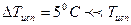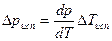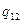I способ: Воспользуемся уравнением Клайперона – Клаузиуса. . Поскольку , то можно воспользоваться приближенным соотношением: , где – удельная теплота парообразования (на 1 моль), 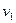– удельный объем пара, 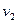– воды (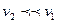). Поэтому

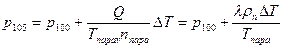, где 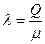- удельная (на единицу массы) теплота парообразования, - молярная масса.

II способ: Рассмотрим цикл Карно для одного моля воды, который испаряется при 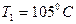(и соответствующем давлении 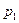) и конденсируется при 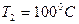(и давлении 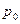). При испарении и конденсаци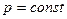и и 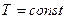, поэтому изотермы будут одновременно и изобарами. КПД цикла Карно будет равен: 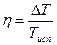. С другой стороны .

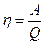Но 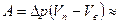{площадь фигуры} , .

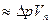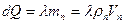Приравнивая два выражения 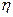, получаем: 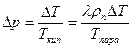. Численное значение .

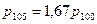37. Определить, насколько изменится температура воды, если ее течением переносит на глубину .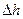

Решение: Будем считать, что слои воды не обмениваются теплом, т.е. 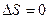для каждого слоя. Изменение температуры при этом можно определить из соотношения: .

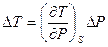Из задачи 15 следует, что 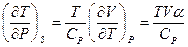, ( 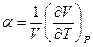- коэффициент теплового расширения).

.

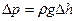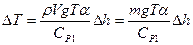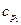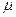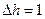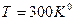Поэтому , где – теплоемкость одного моля воды, - молярная масса. Если км, , то .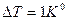

38. Один моль воды охлаждается от температуры 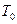до 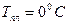и замерзает. При этом тепло отводится к другому молю воды с той же начальной температурой 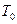с максимальной эффективностью (так, что суммарная энтропия не изменяется). Какое количество воды при этом испарится? Какую работу производит при этом рефрижератор?

Решение: Процессы испарения и конденсации идут при постоянном давлении. При нагревании и охлаждении:

,

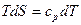следовательно

.

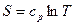Изменения энтропии при испарении и конденсации, соответственно равны ,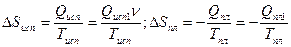

где 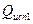и 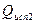– количества теплоты на 1 моль, 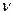- количество молей. Суммарная энтропия по условию равна нулю. Следовательно

,

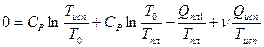откуда можно найти 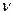. Работа рефрижератора есть разность количества тепла, отданного для нагревания:

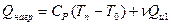
и полученного при охлаждении другого моля (и замораживании его) ;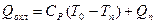

.

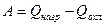39. Поршень с малой теплоемкостью скользит без трения внутри изолированного цилиндра. Объемы 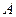и 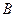наполнены одинаковым количеством идеального одноатомного газа. Начальная температура газа 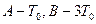. Каково отношение объемов в начальный момент и после установления термодинамического равновесия? Как изменится энтропия одного моля? Какую полезную работу может совершить система при условии, что передача тепла от одного объема к другому обратима?

Решение:

Т.к. все время 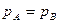, то 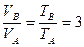в начальный момент. Т.к. 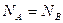и система теплоизолирована, то после установления термодинамического равновесия. 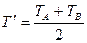={усредненная кинетическая энергия} 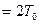и .

И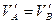зменение энтропии и при постоянном давлении ():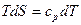

, .

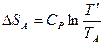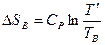Подставляя 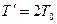, , 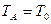, 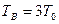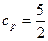получим .

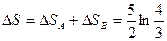Если бы передача тепла происходила обратимо (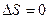), то в соответствии с первым началом термодинамики конечную температуру можно было бы определить из соотношения:

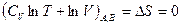
или

, .

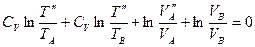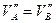Положим , , .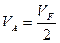

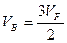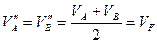Тогда

().

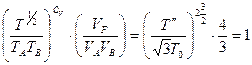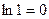Следовательно .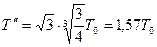

Работа, в силу теплоизолированности системы есть разность внутренних энергий в начале и конце процесса: .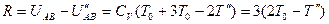

40. Выразить изменение температуры, энтропии и энтальпии через начальный и конечный объем.

Решение:

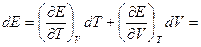{см. задачу 2} =

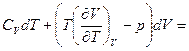{см. задачу 2 для ВДВ газа} = 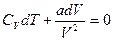(по условию). Отсюда

(*)

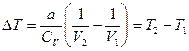Т.к. энтропия – функция состояния, то 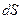– полный дифференциал и, следовательно, 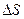не зависит от пути. Пройдем его через точку 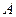(по изохоре и затем по изобаре). Тогда ((см. задачу 2) ).

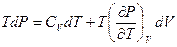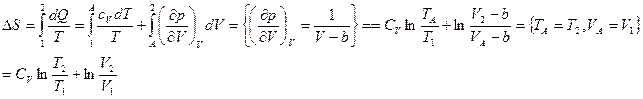
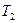( выражается через 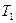по (*)).

Энтальпия 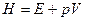, но т.к. 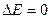, то .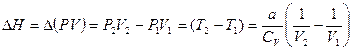

41. Вода проливается через пористую перегородку (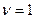) под давлением 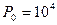атм в большой сосуд с давлением 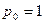атм. Температура воды 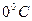, теплота испарения 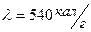, плотность воды постоянна. Какая часть воды испарится?

Решение: Указанный процесс является дросселированием, при котором сохраняется энтальпия (см. задачу 32). Начальная энтальпия воды:

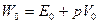, где .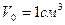

Энтальпия после продавливания:

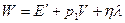, где 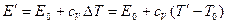, , 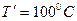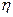- часть воды, перешедшая в пар. По условию 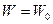. Следовательно

,

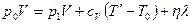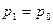. Поэтому

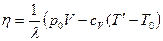. Численное значение для 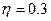(при данных задачи). Следовательно, 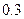воды переходит в пар.

42. Колба наполнена газообразным гелием при температуре 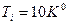(выше критической точки) и теплоизолирована. Газ может медленно вытекать через капиллярную трубку до тех пор пока давление в колбе не станет равным 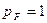атм, а температура 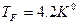(точка кипения гелия). Считая газ идеальным, найти начальное давление газа в колбе 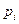, если в конце процесса колба оказывается полностью наполненной жидким гелием. Удельная теплота испарения гелия 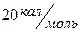, для газообразного гелия .

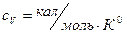Решение: Т.к. система теплоизолирована, то 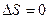. Это изменение энтропии складывается из двух частей – первая - 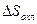– при охлаждении, вторая - при сжижении 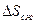. Из первого начала термодинамики для газа:

,

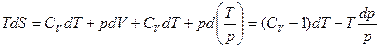откуда

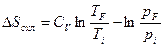(1).

В процессе сжижения температура постоянна и равна 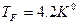. Следовательно 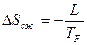(2).

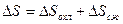(3).

Подставляя (1) и (2) в(3), находим потенцированием: 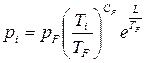. Численное значение равно 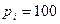атм.

43. Шарообразный спутник радиусом 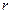, окрашенный в черный цвет, вращается по круговой орбите вокруг солнца. Температура солнца 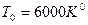. Угол, под которым солнце видно со спутника, 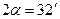. Какова равновесная температура спутника?

Решение: Плотность энергии 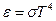(см. задачу 2 для черного излучения в полости). Поток энергии через отверстие в стенке полости с черным излучением 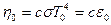(фотоны движутся со скоростью света). В равновесии энергия, получаемая спутником в единицу времени равна излучаемой за то же время. Энергия, излучаемая солнцем в единицу времени равна 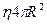( 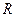– радиус солнца). Следовательно, энергия, получаемая спутником в единицу времени: 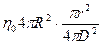( 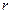– радиус спутника, 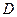– расстояние от солнца до спутника). Энергия, излучаемая спутником 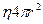. Приравнивая эти величины, находим:

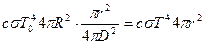.Вводя обозначение 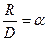- угловой размер, получаем .

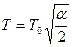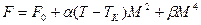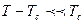44. Свободная энергия ферромагнетика в отсутствие внешнего поля (при , где 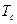-температура Кюри), 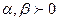и не зависят от температуры, 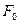- свободная энергия в ненамагниченном состоянии. Найти равновесную намагниченность и температурную зависимость восприимчивости выше точки Кюри.

Решение: 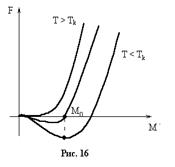В состоянии равновесия 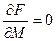, отсюда 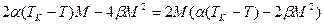, (1)

отсюда 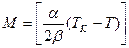при 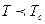Если же 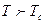, то левая часть (1) отрицательна и тогда у него есть лишь один корень 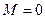. Схематически зависимость F(M) изображена на рис. 16. Если отключить магнитное поле, то к 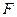добавиться работа по намагничиванию внешним полем 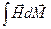. Отсюда значение поля в зависимости от :

.

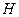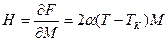Восприимчивость при .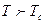

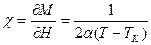45. Рассмотреть термодинамику сверхпроводников.

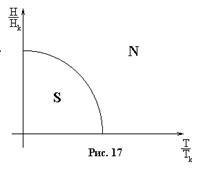Решение: Экспериментально удалось получить зависимость критического поля от температуры – кривую, отделяющую нормальную область от сверхпроводящей: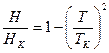

1. 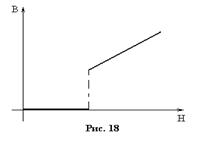В сверхпроводящей фазе всегда 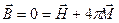. Это значит, что сверхпроводник является диамагнетиком с .

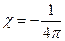В свободной энергии необходимо учесть зависимость как от температуры так и от величины намагниченности

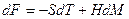
Такой термодинамический потенциал минимален при заданных 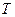и 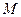. Однако экспериментально контролировать изменение 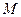трудно, гораздо легче это делать для внешнего поля 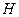. Введем термодинамический потенциал, который минимален при заданных 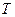и .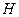

.

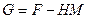Тогда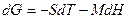

При изменении магнитного поля на величину 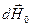источники поля совершают работу над единицей объема

.

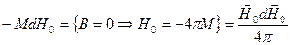Следовательно, при изменении поля т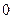о до 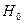источник поля совершает работу .

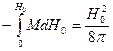Эта работа будет запасена в свободной энергии сверхпроводника

.

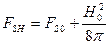В точке переход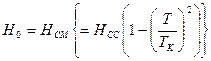а , а 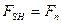– плотности свободной энергии нормального металла.

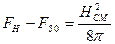(1)

и, следовательно

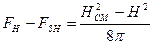(2)

(то же для 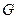)(при фазовом переходе непрерывны как 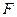так и ).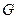

Последняя формула показывает, что при данной температуре и 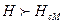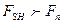и энергетически выгодно нормальное состояние, а при 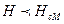– сверхпроводящее (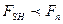). При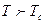 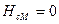и нормальное состояние будет при любом поле. Поскольку 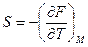, то

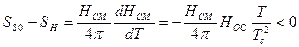
Следовательно, сверхпроводящее состояние более упорядочено (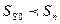). Пр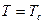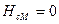и и 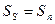. Это значит, что при переходе при 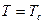не выделяется теплоты (фазовый переход 2-го рода). При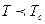 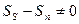и при таком переходе выделяется теплота (фазовый переход 1-го рода). Найдем эту теплоту. При переходе из сверхпроводящей фазы в нормальную 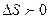(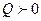)– теплота поглощается и наоборот - при обратном переходе теплота выделяется. В силу непрерывности 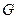вдоль границы сверхпроводник - нормальный металл в состоянии равновесия

.

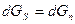
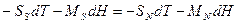Отсюда получаем вышеуказанную кривую фазового равновесия:

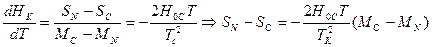
Но 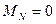, а ,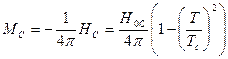

поэтому теплота, выделяющаяся при 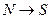переходе:

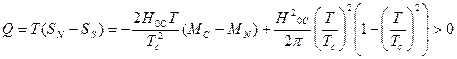(равно нулю если ).

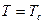Наконец, теплоемкость изменяется скачком при любой температуре:

.

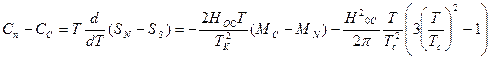Дата добавления: 2015-05-09