Определим АЧХ и ФЧХ фильтра

Где.

.

Системной функцией цифрового фильтра называется отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала

Выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики.

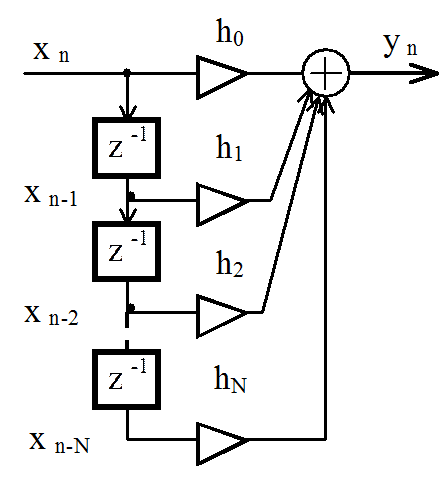
Нерекурсивный цифровой фильтр

2.4. Системная функция цифрового фильтра. Формы программной реализации фильтра

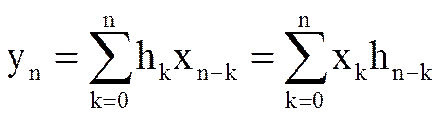
Y(z) = H(z) X(z),

Системная функция H(z) представляет собой Z-преобразование импульсной характеристики цифрового фильтра.

Полюсом системной функции называется значение комплексной переменной z, при котором системная функция H(z) стремится к бесконечности.

Нулем системной функции называется значение комплексной переменной z, при котором системная функция H(z) равна нулю.

Формы программной реализации фильтра:

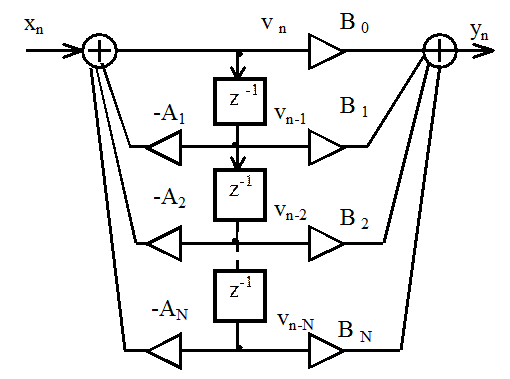
1. Прямая форма

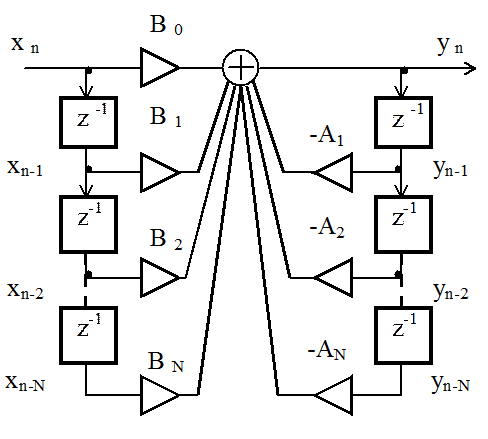
Рисунок 2.5 – Прямая форма программной реализации фильтра

.

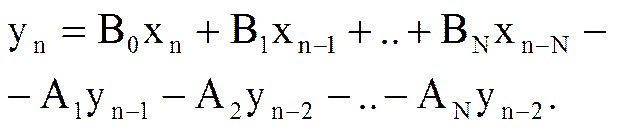
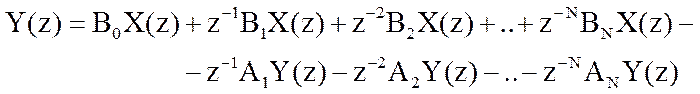
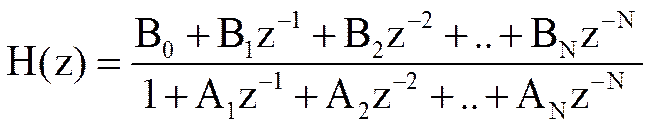Системная функция цифрового фильтра в общем случае представляет собой дробно-рациональную функцию. Полином числителя описывает нерекурсивную часть фильтра, а полином знаменателя – рекурсивную.

Чтобы найти нули системной функции, нужно полином числителя приравнять нулю и найти корни полученного уравнения.

Чтобы найти полюсы системной функции, нужно полином знаменателя приравнять нулю и найти корни полученного уравнения.

Знаки перед коэффициентами A в выражении для системной функции и в разностном уравнении противоположны.

2.Каноническая форма.

Каноническая форма программной реализации фильтра

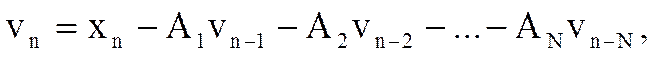
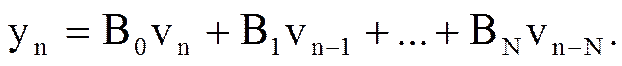
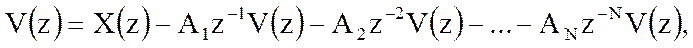
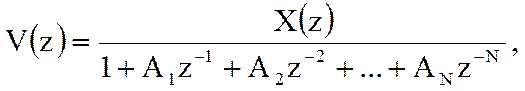
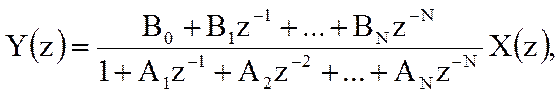
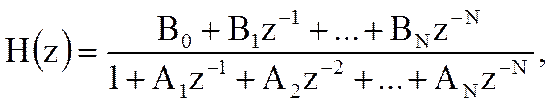
Достоинством канонической формы является в два раза меньшее количество элементов задержки, следовательно, ячеек памяти вычислительного устройства.

Представив системную функцию фильтра в виде произведения или суммы системных функций второго порядка, представим фильтр в виде последовательного или параллельного соединения звеньев второго порядка.

,

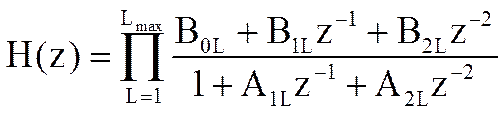
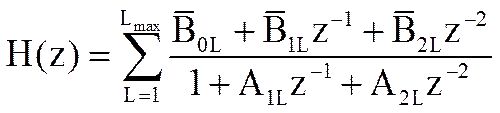где L – порядковый номер звена, L_max – максимальное значение номера звена

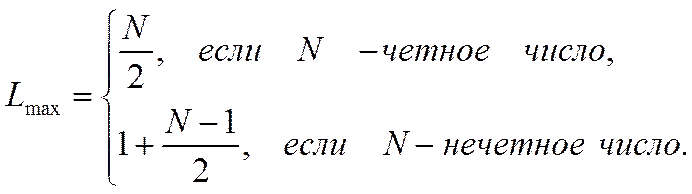
При четном N фильтр состоит из N/2 звеньев второго порядка, при нечетном N фильтр состоит из одного звена первого порядка и (N-1)/2 звеньев второго порядка.

Системная функция звена первого порядка отличается от системной функции звена второго порядка тем, что коэффициенты B₂ и A₂ равны нулю.

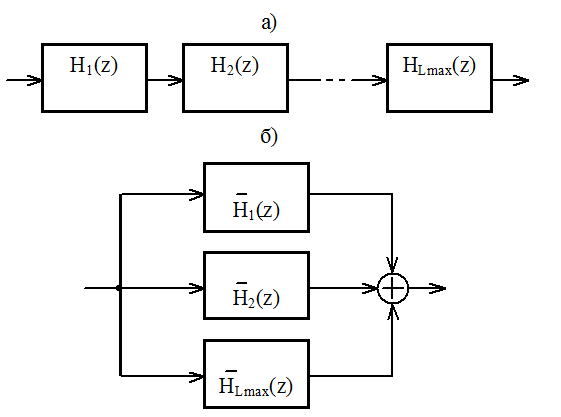
Последовательное (а) и параллельное (б) соединение

звеньев фильтра

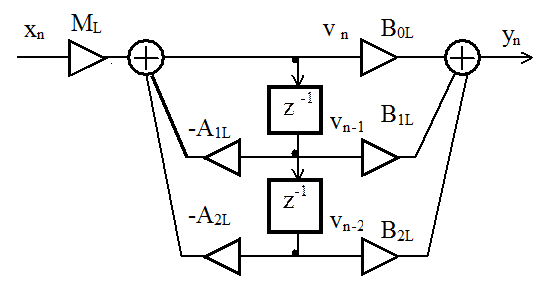
Типовое звено второго порядка

2.5.Частотная характеристика цифрового фильтра

Комплексным коэффициентом передачи фильтра 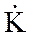является отношение комплексной амплитуды 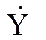выходного сигнала фильтра к комплексной амплитуде входного синусоидального сигнала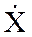

.

Частотной характеристикой цифрового фильтра называется зависимость комплексного коэффициента передачи фильтра от частоты.

Амплитудно-частотной характеристикой (АЧХ) 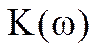называется зависимость модуля комплексного коэффициента передачи от частоты.

.

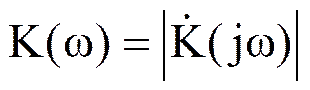Фазочастотной характеристикой (ФЧХ) называется зависимость аргумента комплексного коэффициента передачи фильтра от частоты.

.

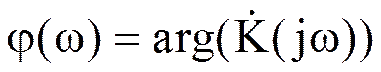Для определения комплексного коэффициента передачи фильтра подадим на вход фильтра с прямой формой реализации комплексный сигнал

.

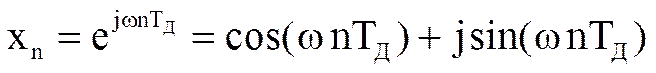Согласно определению комплексного коэффициента передачи комплексный выходной сигнал должен быть равен

.

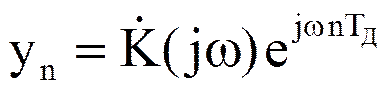Выходной комплексный сигнал фильтра определяется следующим соотношением

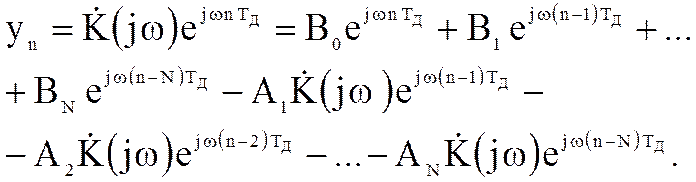
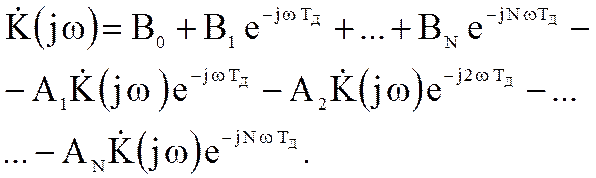
Из последнего соотношения получим

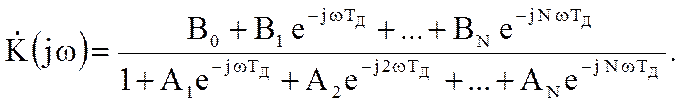
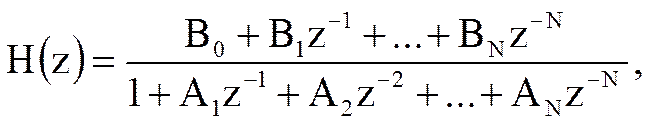
Сравнивая последнее соотношение с выражением для системной функции цифрового фильтра, можно сформулировать правило определения комплексного коэффициента передачи при известной системной функции фильтра: для нахождения комплексного коэффициента передачи нужно в выражении для системной функции заменить z на :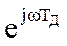

,

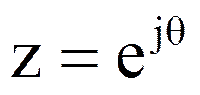где 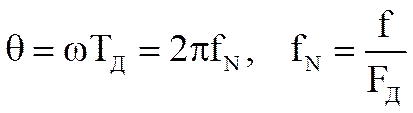- нормированная частота – отношение текущей частоты f к частоте дискретизации F_Д.

2.6. Цифровой резонатор

Цифровой резонатор представляет собой звено второго порядка, у которого коэффициенты системной функции B₁ и B₂ равны нулю.

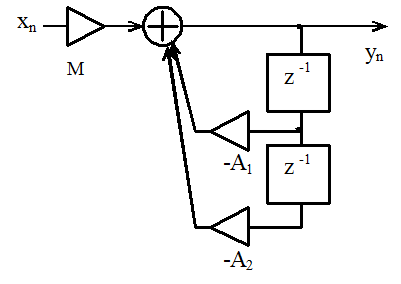
Цифровой резонатор

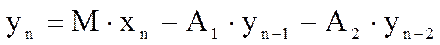
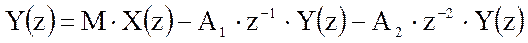
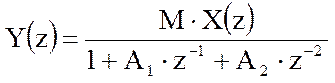
Системная функция резонатора описывается следующим соотношением

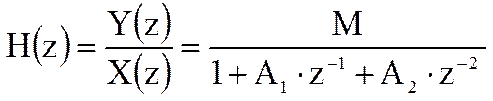
Определим комплексный коэффициент передачи резонатора при A₁=0.

Подставляя в выражение для системной функции 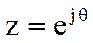, получим

.

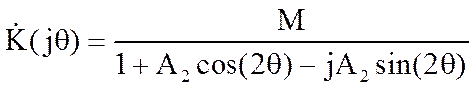Последнее соотношение позволяет определить АЧХ и ФЧХ резонатора:

,

.

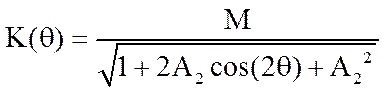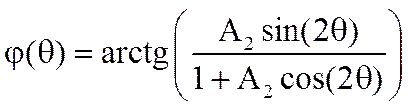При 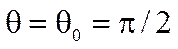резонансный коэффициент передачи равен

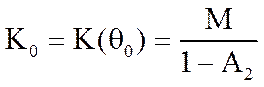
На границах интервала Котельникова

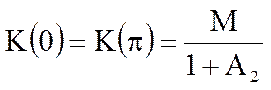
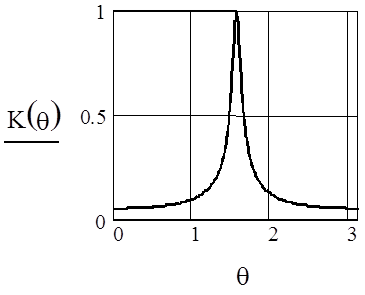
АЧХ резонатора при 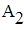=0.9, 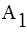=0, M=1-

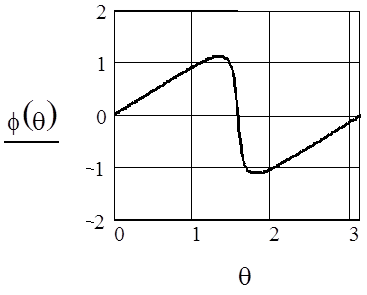
ФЧХ резонатора при =0.9, =0

АЧХ резонатора при A₂ =0.99, A₁=0, M=1-A₂

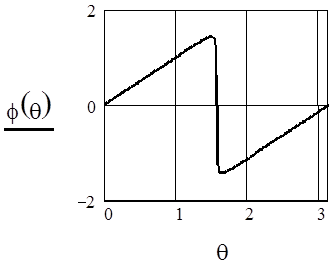
ФЧХ резонатора при A₂=0.99, A₁=0

Сравнение характеристик при разных значениях коэффициента А₂ показывает, что при стремлении А₂ к единице полоса пропускания резонатора уменьшается (резонанс становится более острым) и увеличивается крутизна ФЧХ вблизи резонансной частоты.

Определим полюсы системной функции. Для этого приравняем знаменатель нулю и найдем корни полученного квадратного уравнения

,

.

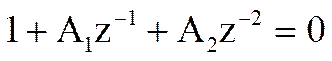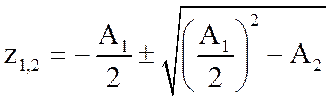В цифровом резонаторе должно выполняться условие

.

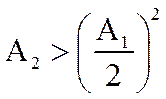Поэтому полюсы системной функции являются комплексно-сопряженными и определяются следующим соотношением

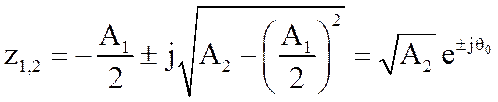, где .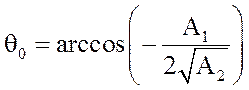

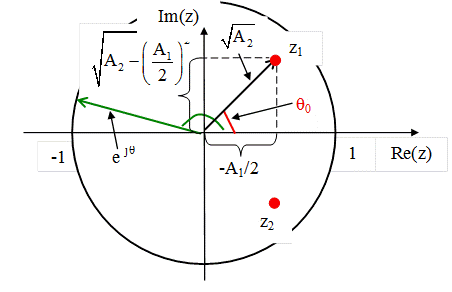
Полюсы системной функции z₁ и z₂

На рисунке показаны полюсы системной функции резонатора на комплексной плоскости z. Окружность единичного радиуса с центром в начале координат является геометрическим местом точек, для которых выполняется условие

.

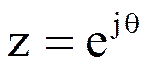При изменении θ от 0 до π частота изменяется от 0 до F_Д / 2. При этом конец вектора 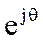перемещается по окружности единичного радиуса. Расстояние конца этого вектора от полюса системной функции минимально при 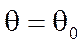, т.е. при 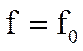, где 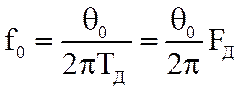- резонансная частота резонатора.

Подставляя в последнее соотношение θ₀ получим

.

Из последнего соотношения видно, что резонансная частота зависит от частоты дискретизации F_Д и коэффициентов системной функции A₁ и A₂. При A₁=0 резонансная частота равна четверти частоты дискретизации, при A₁<0 резонансная частота меньше четверти частоты дискретизации, а при A₁> 0 – больше четверти частоты дискретизации.

Для выяснения влияния коэффициента А₁ на свойства резонатора рассмотрим АЧХ и ФЧХ при А₁<0 и при A₁>0.

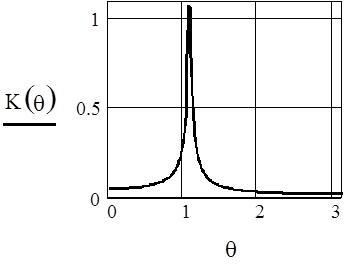
АЧХ резонатора при A₂=0.9, A₁= -0.9, M=1-A₂

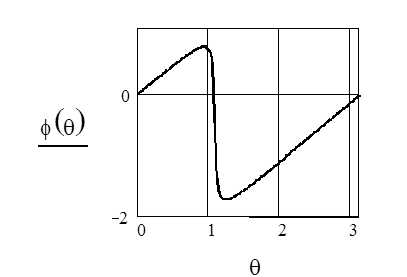
ФЧХ резонатора при A₂=0.9, A₁= -0.9

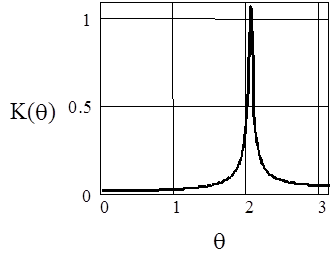
AЧХ резонатора при A₂=0.9, A₁= 0.9, M=1-A₂

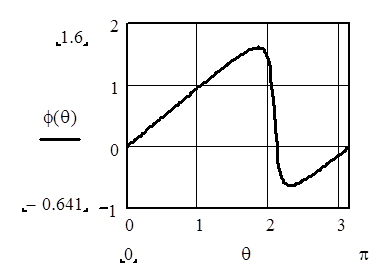
ФЧХ резонатора при A₂=0.9, A₁=0.9

Из приведенных рисунков видно, что коэффициент А₁ сильно влияет на резонансную частоту резонатора. В результате АЧХ и ФЧХ сдвигаются вдоль оси частот. При этом нарушается симметрия АЧХ, становятся различными абсолютные значения максимального и минимального фазового сдвигов, вносимых резонатором, изменяется максимальное значение коэффициента передачи.

2.7. Однородный фильтр

Однородным называется нерекурсивный фильтр, у которого все коэффициенты системной функции одинаковы. Этот фильтр называют также фильтром скользящего среднего.

Однородный фильтр второго порядка

Из рисунка видно, что выходной сигнал фильтра определяется следующими соотношениями

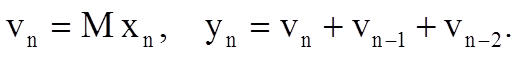
Определим Z-преобразования последовательностей v_n и y_n

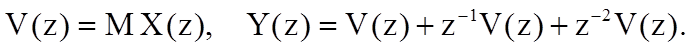
Определим системную функцию фильтра

.

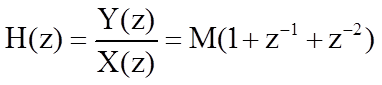Используя подстановку 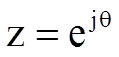, определим комплексный коэффициент передачи

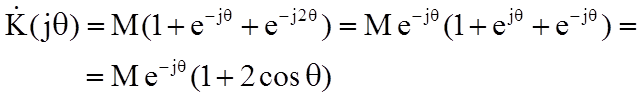
Обозначим

.

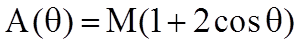Тогда

,

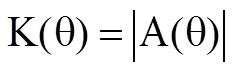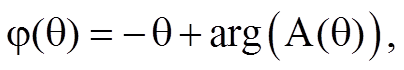
где

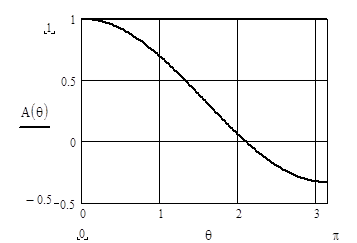
Функция A(θ) однородного фильтра 2-го порядка при M=1/3

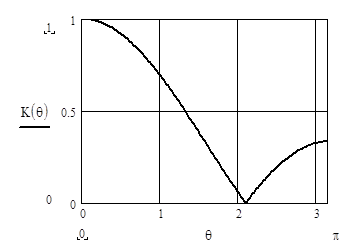
АЧХ однородного фильтра 2-го порядка при M=1/3

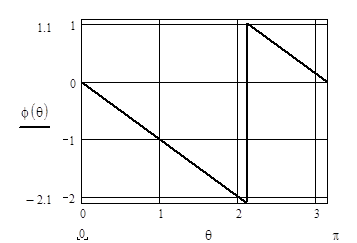
ФЧХ однородного фильтра 2-го порядка

Поскольку ФЧХ принято представлять в интервале значений фазы от –π до π, то соотношение для 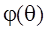корректируется путем прибавления или вычитания 2 π

2.8. Триангулярный фильтр

Последовательное соединение двух одинаковых однородных фильтров порядка N образует триангулярный фильтр порядка 2N.

Последовательное соединение двух однородных фильтров 2-го порядка

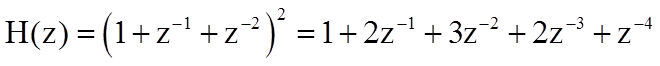
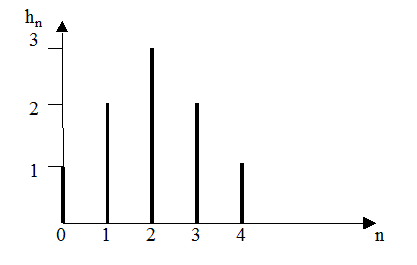
Импульсная характеристика

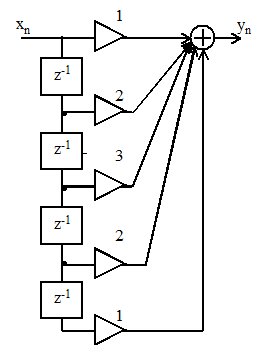
Триангулярный фильтр 4-го порядка

2.9.Устойчивость цифровых фильтров

Критерии устойчивости цифровых фильтров:

1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)

Цифровой фильтр устойчив, если при ограниченном входном сигнале выходной сигнал фильтра также ограничен.

Условие ограниченности входного сигнала определяется соотношением

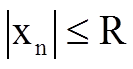
Условием ограниченности выходного сигнала является

.

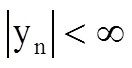2. Критерий оценки устойчивости по импульсной характеристике фильтра

Выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра

.

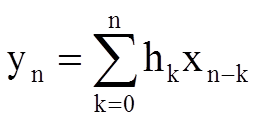Абсолютное значение n-го отсчёта выходного сигнала удовлетворяет неравенству

.

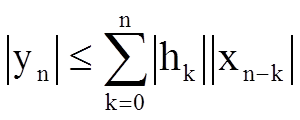При 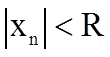справедливо неравенство

.

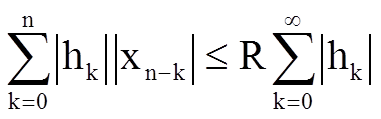Следовательно,

.

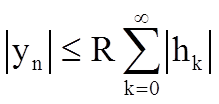Таким образом, чтобы обеспечить выполнение условия 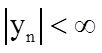, достаточно выполнить условие

.

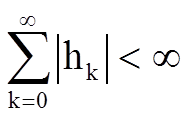Дата добавления: 2015-05-09