Сформируем взвешенную функцию ошибки

Весовая функция определяется следующим соотношением

При g<1 пульсации в полосе пропускания меньше, чем в полосе задерживания, а при g>1 наоборот. При g=1 пульсации в полосе задерживания такие же, как в полосе пропускания.

В случае оптимального решения имеет по крайней мере K+2 экстремума.

Обозначим через 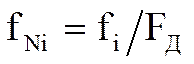, где i= 0,1,..K+1, нормированные частоты экстремумов.

На этих частотах должно выполняться условие

,

где i=0,1,..K+1

Приведенные соотношения представляют собой систему K+2 линейных уравнений с K+2 неизвестными, из которых K+1 неизвестная – коэффициенты C_k аппроксимирующей функции A(θ), а K+2-ая – неизвестная ошибка .

Трудность решения задачи состоит в том, что частоты f_Ni неизвестны.

Поэтому сначала произвольно выбирают K+2 значения частот, решают приведенную систему уравнений, находят C_k и и анализируют ошибку аппроксимации во всем интервале частот. Если в некоторых точках фактическая ошибка превосходит , то выбирают новое множество экстремальных частот путем рассмотрения K+2 точек, где эта ошибка максимальна и имеет чередующийся знак.

В этой процедуре значение на каждом шаге возрастает и, в конце концов, сходится к своей верхней границе.

В соответствии с этим алгоритмом написана машинная программа, нашедшая широкое применение при расчете фильтров.

2.15. Синтез рекурсивных цифровых фильтров методом билинейного Z – преобразования

Передаточная характеристика аналогового фильтра связана с импульсной характеристикой фильтра прямым преобразованием Лапласа

По аналогии с предыдущим соотношением дискретное преобразование Лапласа импульсной характеристики цифрового фильтра определяется выражением

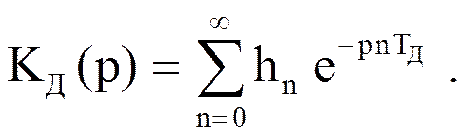
Системная функция цифрового фильтра представляет собой Z-преобразование импульсной характеристики фильтра

Из сопоставления двух последних соотношений следует, что для нахождения H(z) при известной передаточной характеристике аналогового фильтра-прототипа нужно сделать подстановку

Передаточная характеристика аналогового фильтра-прототипа K(p) представляет собой дробно-рациональную функцию, у которой числитель и знаменатель выражаются полиномами относительно комплексной переменной p.

где n<m

Последняя подстановка не позволяет получить системную функцию в виде дробно-рациональной функции с полиномами относительно комплексной переменной z в числителе и знаменателе.

Чтобы найти системную функцию, воспользуемся приближенным выражением для ln(z)

.

Следовательно,

Последнее соотношение получило название билинейного Z- преобразования.

Докажем, что билинейное Z-преобразование преобразует устойчивый аналоговый фильтр в устойчивый цифровой фильтр. Для этого из последнего соотношения выразим z через p = s + jw

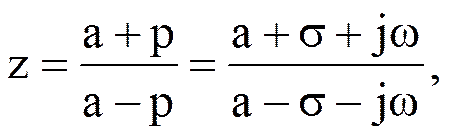
где .

Откуда

Из последнего соотношения видно, что при s<0 (условие устойчивости аналогового фильтра-прототипа) (условие устойчивости цифрового фильтра). На рисунке показаны затемненные области устойчивости аналогового фильтра - прототипа в плоскости p и цифрового фильтра в плоскости z.

Области устойчивости цифрового фильтра и

аналогового фильтра-прототипа

Таким образом, билинейное Z-преобразование преобразует левую полуплоскость плоскости p в круг единичного радиуса с центром в начале координат.

Найдем связь между цифровыми и аналоговыми частотами, на которых коэффициенты передачи цифрового фильтра и аналогового фильтра-прототипа одинаковы.

Используя билинейное Z – преобразование, можно выразить передаточную характеристику аналогового фильтра через системную функцию цифрового фильтра

Следовательно, комплексный коэффициент передачи аналогового фильтра можно выразить через системную функцию цифрового фильтра

С другой стороны, комплексный коэффициент передачи цифрового фильтра связан с системной функцией следующим соотношением

Из двух последних соотношений видно, что коэффициенты передачи цифрового фильтра и аналогового фильтра-прототипа равны при выполнении условия

Преобразуя последнее соотношение, получим

*

Таким образом, частота аналогового фильтра – прототипа связана с частотой цифрового фильтра при равенстве их комплексных коэффициентов передачи нелинейной зависимостью.

Однако, чем выше частота дискретизации, тем ближе частота аналогового фильтра – прототипа к частоте цифрового фильтра.

Если частота цифрового фильтра удовлетворяет условию , то с погрешностью не более 5% можно считать аналоговую и цифровую частоты одинаковыми.

Указанная нелинейная зависимость вызывает сжатие АЧХ цифрового фильтра по сравнению с АЧХ аналогового фильтра – прототипа.

АЧХ цифрового фильтра и аналогового фильтра – прототипа при использовании билинейного Z – преобразования

Чтобы избежать сужения полосы пропускания цифрового фильтра аналоговый прототип рассчитывают, исходя не из граничных частот полосового фильтра, а из частот, определенных по формуле * при подстановке в эту формулу граничных частот полосового фильтра. При этом получают цифровой фильтр с заданными граничными частотами.

Задача.

Требуется найти цифровой эквивалент аналоговой RC – цепи, представленной на рисунке

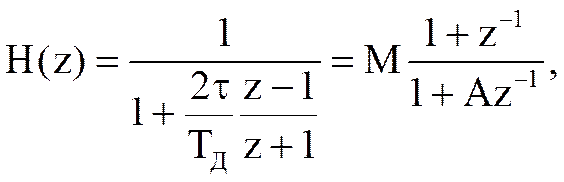
где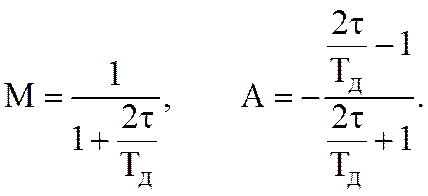

Дата добавления: 2015-05-09