Формирование остатка двоичного числа по модулю 3

Контроль сложения на основе остатков по мод 3

Контроль сложения на основе остатков по М 2

Контроль сдвига

Операция сдвига проверяется также с помощью схем контроля по четности. Для этой цели на выходе регистра сдвига РГА[0:n] устанавливается триггер со счетным входом, который представляет собой сумматор по М 2 накапливающего типа. Триггер контроля перебросится столько раз, сколько единиц будет в коде. На прямом выходе триггера будет значение, соответствующее М2 (РГА[0:n]).

Рассмотрим математическую постановку задачи. Ищем

S = A + B.

Представим слагаемые и сумму в векторной записи как последовательность двоичных коэффициентов:

S = { S_n , S_n-1, … S₁ , S₀ }

A = { a_n , a_n-1, … a₁ , a₀ }

B = { b_n , b_n-1, … b₁ , b₀ }

C = { c_n , c_n-1, … c₁ , c₀ } – перенос

S_i = a_i Å b_i Å c_i

S₁ = a₁ Å b₁ Å c₁

_{………….}

S_k = a_k Å b_k Å c_k

S_n Å S_n-1 Å … S₁ Å S₀ = (a_n Å a_n-1 Å … a₁ Å a₀) Å (b_n Å b_n-1 Å … b₁ Å b₀) Å (c_n Å c_n-1 Å … c₁ Å c₀)

Приведем это соотношение к более компактной записи

M2 (S) = M2 (A) Å M2 (B) Å M2 (C) (1.13)

В соответствии с этими выражениями построена схема контроля по четности, обеспечивающая обнаружение ошибки при выполнении операции сложения. Как следует из (9.5), необходимо также предусмотреть суммирование по мод 2 цифр переносов, которые возникают между разрядами при суммировании.

Однако, как отмечалось выше, данный метод контроля, основанный на использовании операций с остатками суммирования по мод2, обеспечивает обнаружение лишь нечетных ошибок.

Идея этого способа состоит в том, что каждому слагаемому ставится в соответствие некоторый контрольный код, который представляет собой остаток этого числа по модулю 3. Одновременно с суммированием, выполняется суммирование контрольных кодов, которое позволяет обнаружить ошибку (это же относится и к любой другой арифметической операции).

S = A+B; A + B = 3 (a + b) + R (A) + R (B) (1.14)

R(A) – остаток числа А по мод 3.

R(A) – остаток числа В по мод 3.

A = a × 3 + R (A)

B = b × 3 + R (B) a,b - целые числа или 0

R (A+B) = R (A) + R (B) = g × 3 + R [ R (A) + R (B) ], где

R (A) и R(B) Î { 0,1,2 }, g Î { 0,1 }, R (A) + R (B) = [0..4] подставив в (9.6) получим A + B = 3 (a + b + g) + R [ R)A) + R(B) ] и

R (A+B) = R [ R)A) + R(B) ] (1.15)

Соотношение (1.15) является математическим решением задачи контроля и на ее основе строится логическая схема контроля.

Из теории известно, что контроль по модулю 3 обнаруживает все одиночные и часть двойных ошибок.

Рассмотрим двоичное число А₂, ½A½> 1

A= a_n× 2ⁿ + a_n-1× 2^n-1 + …+ a₁× 2¹ + a₀× 2⁰

От этого двоичного числа перейдем к четверичному числу:

A = a_m × 4^m + a_m-1 × 4^m-1 + …+ a₁ × 4¹ + a₀ × 4⁰

Каждая четверичная цифра числа получается из 2-х разрядов двоичного числа.

m = (n+1) /2 при ``n`` нечетном и m = n/2 при ``n`` четном

a_m = a_n× 2 + a_n-1 a₀= a₁× 2 + a₀

a_m-1 = a_n-2× 2 + a_n-3 (1.16)

Пример:

2¹2⁰ 2¹2⁰ 2¹2⁰ 2¹2⁰

A₂ = 1 0 1 1 0 1 0 1 = 181₁₀

4³ 4² 4¹ 4⁰

Цифры двоичного числа А разбиты на пары, которые соответствуют четверичным цифрам. Над двоичными цифрами каждой пары проставлены их двоичные веса, чтобы было легче определить четверичные цифры.

A₄ = 2 × 4³ + 3 × 4² +1 × 4¹ +1 × 4⁰ = 128 + 48 + 4 + 1 = 181₁₀

R (A) = R (a_m× 4^m) + R (a_m-1× 4^m-1) +… + R (a_i× 4ⁱ) + R (a₀)

так как остаток от суммы равен сумме остатков слагаемых, разложим бином 4ⁱ в ряд:

4ⁱ = (3 + 1)ⁱ = 3ⁱ + C₁× 3 ^i-1 + C₂× 3 ^i-2 + …+ C_i-1× 3 + 1

где C₁, C₂, …C_i-1 – биномиальные коэффициенты,

R (4ⁱ) = 1 – остаток по модулю 3 величины 4ⁱ, тогда

R (A) = R (a_m) + R (a_m-1) +… + R (a₁) + R (a₀)

R (A) = R (a_m +a_m-1 +… + a₁ + a₀)

Остаток по модулю 3 некоторого числа А равен остатку суммы его четвертичных цифр.

Вычислим остаток по мод3 двоичного числа:

А₂ = 0 1 1 0 1 1 0 1 1 0.

Пользуясь соотношениями (1.16), переведем его в четверичный код:

А₄ = 1 2 3 1 2 - четверичное число.

Преобразуем это число, заменив каждую цифру остатком по мод 3:

R_I(A) = (1 2 0 1 2) – остаток по мод 3 каждой четверичной цифры числа А (остаток под мод 3 первого ранга).

R_II(A) = (1 2 0) – попарное суммирование цифр остатков по мод 3 первого ранга (остаток второго ранга).

R_III(A) = (1 2) – результат попарного суммирования цифр предыдущего остатка (остаток третьего ранга).

R_IV(A) =0 – окончательная сумма по мод 3 двоичного числа А₂.

Проанализировав процесс формирования остатка по мод 3, найдем логические выражения на основании которых можно построить соответствующую логическую схему (операция сложения заменяется логической операцией).

Таблица 1.8

a1	a0	a	R|(a)

Запишем в таблице истинности (табл. 1.8) правила перехода от пары двоичных цифр ``a<sub>1</sub>a<sub>0</sub>`` к четверичной цифре ``a<sub>0</sub>`` и к остатку R(a₀).

Запишем формальные выражения

a₀:= если (a₁ & a₀ ) то 3, иначе

если (a₁ & 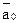) то 2, иначе

если ( & a₀) то 1, иначе

если ( & 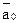) то 0;

R_I (a₀):= если ( & 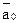) Ú (a₁ & a₀ ) то 0, иначе

если (a₁ & 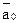) то 2, иначе (1.9.)

если ( & a₀) то 1.

Выражение (1.9.) представляет собой логические правила формирования не только любой цифры остатка по мод 3 1-го ранга, но является справедливым и для получения цифр остатков всех последующих рангов. Как следует из примера и табл. 1.8, формирование каждой цифры остатка следующего ранга происходит из соответствующей пары цифр предыдущего ранга. Каждая их этих цифр может иметь одно из трех значений: 0,1,2.

Таблица 1.9.

RI(i)	RI(i-1)	RII(j)

В соответствии с этими соображениями составим таблицу истинности (табл. 9.3), в которой отображена логическая зависимость между парой цифр остатка 1-го ранга и соответствующей цифрой остатка по мод 3 2-го ранга. Добавим, что эта таблица справедлива и для формирования цифр остатков последующих рангов.

На основании этой таблицы можно составить логические выражения для формирования остатков 2-го уровня и построить логические схемы.

Способ контроля правильности выполнения операции сложения на основе остатков по модулю 3 достаточно сложен, но применяется, если нужно обеспечить очень высокую достоверность вычислений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Имеется некоторое десятичное число А= − 0.75. Преобразовать в двоичный код и записать в двоичном формате для │А│<1.

2. Записать целое десятичное число В= − 346 в двоичном формате для │А│>1.

3. Записать десятичное число А= 437∙10^-3 в двоичном коде в формате с плавающей точкой в нормализованном виде.

4. Преобразовать десятичное число В= − 0.43 в двоичный код и записать в прямом, обратном и дополнительном кодах.

5. Преобразовать десятичные числа (простые дроби) А= 31/32, В= 17/64 в двоичный код и выполнить операцию вычитания по алгоритмам ПП, ПО, ПД.

6. Выполнить операцию вычитания для чисел А, В из пункта 5 по алгоритмам ДД, ОО.

7. Для десятичных чисел А=57939, В=27405 выполнить операцию сложения в двоично-десятичном коде 8421.

8. Для десятичных чисел А=57939, В=27405 выполнить операцию вычитания в двоично-десятичном коде 8421 по алгоритму ПД.

9. Для двоичных чисел А=0.0110101 В=0.11011101 выполнить операцию сложение с контролем на основе остатков по модулю 2.

10. Сформировать остаток двоичного числа по модулю 3 для чисел А₁=101100010111 и А₂= 110111001011.

Дата добавления: 2015-05-09