Решение типовых задач

Пример 1. Привести выражение 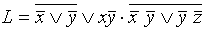к ДНФ, а затем сократить ее (если это возможно).

Решение. “Понижаем” отрицания по правилу де Моргана. Получаем 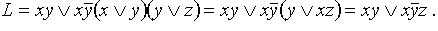По правилу Блейка (имеются дизъюнктные слагаемые, содержащие у и 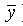) к последнему выражению можно добавить слагаемое x z, котороепоглотит второе слагаемое в L.

Ответ: L = xy Úxz

В задачах 1–10, б) надо просто применять правило Блейка, а затем уже правило поглощения

Теорию, применяемую к задачам 11–20, подробно обсуждали в разд. 3, 6, поэтому ограничимся решением примеров.

Пример 2а. Дана ДНФ 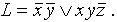. Требуется для этой функции найти полином Жегалкина и перейти от ДНФ к КНФ, а затем и к СКНФ. Сначала найдем полином Жегалкина (вторым способом). Для этого ставим двойное отрицание и по правилам де Моргана “убираем” дизъюнкцию, потом “убираем” отрицания по правилу 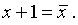. После этого раскрываем скобки, учитывая при этом, что четное число слагаемых (по модулю 2) равно 0, а нечетное – одному такому слагаемому. Тогда

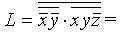((x+ 1)(y +1)+1)(xy (z +1)+1)+1=(xy+x+y+ 1+1)(xyz+xy+ 1)+1=

= (xy+x+y)(xyz+xy+ 1)+1= xyz + xyz + xyz + xy+xy+ xy+ xy +
+ x+ y+ 1= xyz+x+y+ 1.

Последнее выражение и является полиномом Жегалкина.

Для того чтобы перейти к КНФ для выражения L (в соответствии с разд. 3) ставим над L два отрицания и, оставляя временно верхнее отрицание безизменения, приводим оставшееся выражение к ДНФ. Затем по правилу де Моргана получаем КНФ. Таким образом, можем получить

.

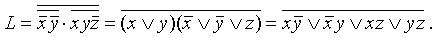Далее по правилу Блейка можем из последнего выражения исключить yz, тогда получим: 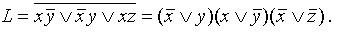. Это и есть КНФ.

Чтобы из последнего выражения получить СКНФ, нужно в первой и второй дизъюнкции добавить 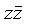, а в третьей – 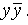Затем воспользуемся распределительным законом:

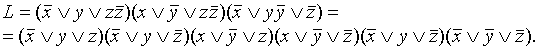
Последнее выражение и есть СКНФ.

Пример 2б. Пусть имеется выражение . Требуется записать L в виде ДНФ, а затем перейти к СДНФ.

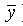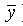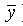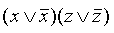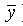Ясно, что ДНФ можно получить простым раскрытием скобок. В обеих скобках есть , которое поглощает слагаемые, содержащие , поэтому. Это и есть ДНФ. Для того чтобы получить СДНФ, умножаем на , а умножаем на (y Ú )и раскрываем скобки. Тогда

.

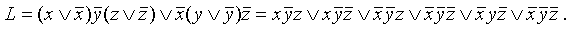С самого начала надо позаботиться о правильном порядке переменных, что требуется для СДНФ, но последнее выражение еще не является СДНФ, так как содержит два одинаковых слагаемых. После уничтожения одного из них получим окончательный ответ:

Разберем пример решения задач типа 21–30.

Пример 3. Пусть требуется для функции

f(x, y, z) = (x ~ z) | ((x y) ~ (y z)):

а) составить таблицу истинности;

б) написать для неё СДНФ или СКНФ (если это возможно);

в) сократить СДНФ по карте Карно;

г) найти по таблице истинности полином Жегалкина.

Решение:

а) в таблицу истинности данной функции полезно включить таблицы истинности промежуточных функций:

xyz	x ~ z	x y	y z	(x y) ~ (y z)	(x~ z)|((x y) ~ (yz)

б) составить СДНФ и СКНФ по полученной таблице. В соответствии с теорией разд. 4 СДНФ составляется по единицам таблицы истинности, причем если f(x, y, z) = 1, то если х = 0, в соответствующей конъюнкции СДНФ берется , а если х = 1 в СДНФ берется х. Аналогично поступают и с другими переменными, поэтому СДНФ для данной функции имеет вид:

.

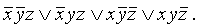СКНФ составляется по нулям таблицы истинности, т. е. если
f(x, y, z) = 0 и х = 0, то в соответствующей дизъюнкции берётся х, а если х = 1, то . Таким образом, СКНФ для данной функции имеет вид:

.

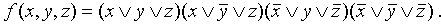
Заметим, что по определению СДНФ и СКНФ, переменные (в каждой конъюнкции и дизъюнкции соответственно) должны следовать в одинаковом порядке;

в) составим полином Жегалкина по таблице истинности. Напишем его сначала с неопределёнными коэффициентами:

f(x, y, z) = a₀ + a ₁ x+ a ₂ y+ a ₃ z+ a ₄ xy+ a ₅ xz+ a ₆ yz+ a ₇ xyz.

Подставим в него по очереди все 8 наборов переменных и найдём коэффициенты полинома Жегалкина.

• x = 0, y = 0, z = 0: a ₀ = 0;
• x = 0, y = 0, z = 1: a ₃ = 1;
• x = 0, y = 1, z = 0: a ₂ = 0;
• x = 0, y = 1, z = 1: a ₂ + a ₃ + a ₆ = 1, a ₆ = 0;
• x = 1, y = 0, z = 0: a ₁ = 1;
• x = 1, y = 0, z = 1: a ₁ + a ₃ + a ₅ = 0, a ₅ = 0;
• x = 1, y = 1, z = 0: a ₁+ a ₂ + a ₄ = 1, a ₄ = 0;
• x = 1, y = 1, z = 1: a ₀ + a ₁ + a ₂ + a ₃ + a ₄ + a ₅ +a ₆ + a ₇ =0.

Так как a ₀ =a ₂ =a ₄ =a ₅ =a ₆ = 0, тогда a ₁ +a ₃ +a ₇ = 0, откуда a ₇ = 0, и полином Жегалкина для данной функции имеет вид: f (x, y, z) = x+ z (для данной функции у является фиктивной переменной);

г) составим теперь для данной функции карту Карно и сократим её. Сначала составим таблицу:

Откуда f(x, y, z) = 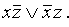. Опять оказалось, что у – фиктивная переменная.

Пример 4 .

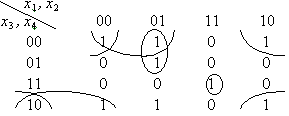
Получаем всего 4 объединения, т. е. 4 конъюнкции в ДНФ: f = (x₁,x₂, x₃,x₄) =

Заметим, что при правильно составленном объединении единиц правило Блейка может привести только к ДНФ с тем же числом символов переменных (в нашем примере их 11).

Пример 5. Пусть дан ориентированный граф (рис. 12), причем ребра a,b,h являются ориентированными (их направление указано стрелками), а остальные ребра не ориентированы. Требуется методами булевой алгебры найти пути и сечения между вершинами 2 и 4.

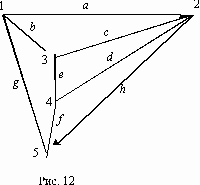
Составляем структурную матрицу S,затем вычеркиваем из нее 4-ю строчку и 2-й столбец (тем самым получаем минор М (4, 2)):

.

Раскрытие определителей производится по известному правилу: определитель равен сумме (в данном случае дизъюнкции) произведений элементов, умноженных на свои алгебраические дополнения (в данном случае просто миноры). При этом для определителей 3 -го порядка можно пользоваться и правилом треугольника.

Тогда получаем

Искомые пути, расположенные в порядке прохождения ребер:

П ₂₄ = d Ú hf Ú ce Ú hgbe.

Сечения же получатся отрицанием этих путей. Применяя правила де Моргана (заменяя конъюнкцию на дизъюнкцию и наоборот), затем раскрывая скобки, получаем: (знаки отрицания опущены во всех равенствах, кроме 1-го):

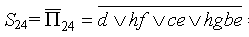= d (hÚ f)(cÚe)(hÚgÚbÚe)

S ₂₄ = d (h Ú f)(e Ú ch Ú cg Ú cb) = d (he Ú ch Ú cgh Ú сbh Ú fe f Ú ch Ú fcg Ú fcb),

или, применяя в скобках правило поглощения, получаемÚ

S ₂₄ = d (he Ú ch Ú fe f Ú cg Ú fcb),

S ₂₄ =dhe Ú dch Ú dfе Ú dfcg Ú dfcb.

Дата добавления: 2015-05-09