
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
РЫБИНСК 2007 2 страница
|
|
|
|
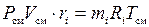 .
.
Последнее выражение преобразуем к виду
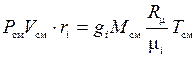 .
.
Если записать выражения для каждого компонента смеси, а затем просуммировать, получим
 ;
; 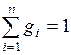 ,
,
тогда
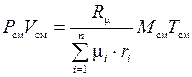 .
.
Таким образом
 , а
, а  . (1.19)
. (1.19)
Получим расчетные зависимости для 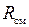 и
и 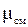 , если смесь задана массовыми долями
, если смесь задана массовыми долями 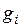 . Запишем уравнение состояния для М кг газовой смеси и для
. Запишем уравнение состояния для М кг газовой смеси и для  кг компонентов газов, входящих в смесь, через их парциальные объемы:
кг компонентов газов, входящих в смесь, через их парциальные объемы:
 ;
;  .
.
Если записать второе выражение для каждого компонента, а затем их просуммировать, то получим
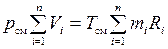 .
.
Перепишем его в виде
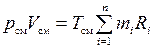 .
.
Поделив последнюю зависимость на уравнение состояния смеси для М кг, получим зависимость для расчета R см и mсм через массовый состав:
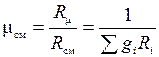 ;
; 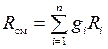 . (1.20)
. (1.20)
Последние выражения позволяют по объемным долям и молекулярным массам компонентов рассчитать газовую постоянную смеси и среднюю молекулярную массу.
Зная соотношения между массовыми и объемными долями газов, можно рассчитать парциальные давления
 ;
; 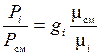 или
или 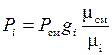 . (1.21)
. (1.21)
Запишем закон Бойля-Мариотта для i -го компонента и всей смеси
 ,
,
откуда
 ,
,
тогда
 или
или 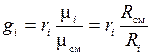 . (1.22)
. (1.22)
Приравнивая зависимости (1.21) и (1.22), получим формулы перевода массовых долей в объемные и наоборот:
 ;
; 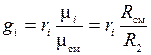 . (1.23)
. (1.23)
Плотность газовой смеси:

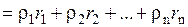 ,
,
таким образом,
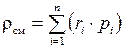 . (1.24)
. (1.24)
Выразим 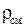 через массовый состав смеси:
через массовый состав смеси:
 ,
,
следовательно, 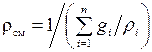 .
.
1.3. Теплоемкость смеси газов
Пусть известны ci – зависимость массовых теплоемкостей компонентов от температуры
 .
.
Для одного килограмма газовой смеси массовая теплоемкость может быть рассчитана по формуле
 . (1.25)
. (1.25)
Или с учетом зависимости теплоемкостей от температуры
 .
.
Если задан объемный состав, то удобней пользоваться объемными теплоемкостями:
для 1 м3 компоненты: 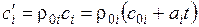 ,
,
для 1 м3 смеси:  . (1.26)
. (1.26)
Или с учетом зависимости от температуры:
 . (1.27)
. (1.27)
1.4. Энтропия газовой смеси
Воспользовавшись объединенным выражением первого и второго начал термодинамики, запишем
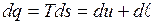
или
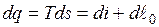 .
.
Распишем выражения, входящие в правые части
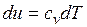 ;
;  ;
;  ;
;  .
.
Тогда после подстановки получим
 ;
;  .
.
Предполагая газ совершенным, а, следовательно, подчиняющимся уравнению состояния в форме Клапейрона-Менделеева, преобразуем, правые части к виду удобному для интегрирования (исключим лишнюю переменную)
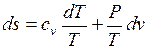 ;
; 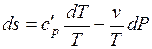 .
.
Запишем уравнение состояния и выразим из него давление и удельный объем
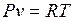 ;
;  ;
;  или
или 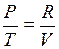 ;
; 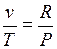 .
.
После подстановки в (1.26) и (1.27)
 ;
;  .
.
Проинтегрируем (1.26) и (1.27) от состояния 1 до состояния 2:
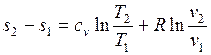 ; (1.28)
; (1.28)
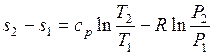 . (1.29)
. (1.29)
Если в качестве независимых переменных будут выбраны  и
и  , то выражение для расчета изменения энтропии в политропных процессах может быть преобразовано к виду
, то выражение для расчета изменения энтропии в политропных процессах может быть преобразовано к виду
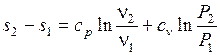 . (1.30)
. (1.30)
Известно, что энтропия является аддитивной функцией состояния, а, следовательно, для системы, состоящей из «n» частей, должны вычисляться соотношения
 . (1.31)
. (1.31)
С другой стороны энтропия может быть рассчитана по зависимости, в которой в явной форме аддитивность не отражена
 . (1.32)
. (1.32)
По своей сути выражения (1.32) и (1.31) эквивалентны.
Энтропия смеси идеальных газов представляет собой сумму энтропий газов, входящих в смесь
 . (1.33)
. (1.33)
Для газа с параметрами  и
и 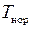 следует, что его энтропия в соответствии с (1.29) равна
следует, что его энтропия в соответствии с (1.29) равна
 , (1.34)
, (1.34)
где 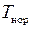 – температура нормировки;
– температура нормировки;  – парциальное давление;
– парциальное давление;  – давление нормировки.
– давление нормировки.
Парциальное давление компонента в смеси можно определить по ранее приведенной зависимости
 .
.
Тогда второе слагаемое правой части выражения (1.34) может быть сведено к виду
 .
.
Следовательно, выражение для энтропии газовой смеси (1.33), представленное в виде аналогичном (1.31), можно переписать
 . (1.35)
. (1.35)
Выражение, стоящее в скобках в правой части (1.35), представляет собой энтропию 1 кг компонента при параметрах смеси, которую можно обозначить, как 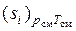 , а последнюю сумму можно определить как приращение энтропии в процессе необратимого смешения идеальных газов, входящих в смесь. Так как по смыслу величина
, а последнюю сумму можно определить как приращение энтропии в процессе необратимого смешения идеальных газов, входящих в смесь. Так как по смыслу величина  , то выражение (1.35) может быть переписано в виде
, то выражение (1.35) может быть переписано в виде
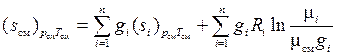 . (1.36)
. (1.36)
Учитывая формулу соотношения массовых и объемных долей 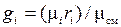 , перепишем (1.36)
, перепишем (1.36)
 . (1.37)
. (1.37)
Из (1.37) следует, что смешение различных газов при 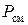 ,
,  приводит к возрастанию энтропии на величину энтропии смешения
приводит к возрастанию энтропии на величину энтропии смешения
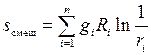 (1.38)
(1.38)
или для отдельно взятого i -го компонента
 . (1.39)
. (1.39)
Выражение (1.32) учитывает возрастание энтропии i -го компонента за счет необратимости процесса смешения.
1.5. Задание для самостоятельного решения
Исходные данные для выполнения индивидуального задания необходимо взять из табл. 1 Приложения 1 в соответствии со своим вариантом.
Газовая смесь задана одним из выше рассмотренных способов. Известны давление смеси  , Па, температура смеси
, Па, температура смеси  , К и объем смеси
, К и объем смеси 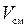 , м3.
, м3.
Требуется определить:
– состав смеси через другие доли;
– газовые постоянные компонентов и смеси;
– кажущуюся молекулярную массу смеси через объемные и массовые доли;
– массу смеси и входящих в нее компонентов;
– парциальные объемы и плотности компонентов;
– плотности компонентов и смеси при нормальных условиях через объемные и массовые доли;
– мольную, объемную и массовую изобарную и изохорную теплоемкость для вышеуказанной температуры;
– средние мольные, объемные и массовые изобарные и изохорные теплоемкости для заданного интервала температуры;
– затраты тепла на изобарное нагревание (охлаждение) четырех молей, 10 м3 и 10 кг смеси в заданном интервале температуры;
– энтропию компонентов входящих в смесь и энтропию газовой смеси в целом.
1.6. Пример выполнения индивидуального задания
Дано:
1. Смесь задана следующим объемным составом.
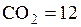 %;
%;  %;
%; 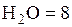 %,
%,
или в объемных долях
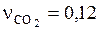 ;
;  ;
;  .
.
2. Температура, при которой определяется истинная теплоемкость смеси,  °С (2273 К).
°С (2273 К).
3. Интервал температур, для которого определяется средняя теплоемкость смеси:
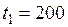 °С (
°С (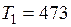 К);
К);
 °С (
°С ( К).
К).
Решение.
1. В исходных данных смесь газов задана объемными долями. Воспользовавшись формулой раздела 1.2 определим через массовые доли состав смеси
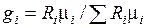 .
.
Запишем молярные массы компонентов:
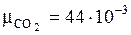 кг/моль;
кг/моль; 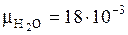 кг/моль;
кг/моль;
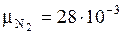 кг/моль;
кг/моль; 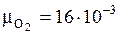 кг/моль;
кг/моль;
Тогда массовая доля углекислого газа:
 .
.
Аналогично находим массовые доли остальных компонентов:
 ;
;  ;
; 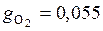 .
.
Сумма массовых долей:
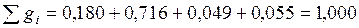 .
.
2. Газовые постоянные компонентов определяем по формуле:
 , Дж/(кг·К);
, Дж/(кг·К);

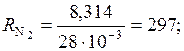
 ;
; 
3. Газовую постоянную смеси находим по формуле (1.16) раздела 1.2:
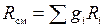 ;
;
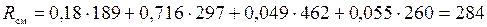 Дж/(кг·К).
Дж/(кг·К).
4. Найдем значение кажущейся молекулярной массы смеси, заданной объемными долями, формуле (1.18):


 кг/моль.
кг/моль.
Если смесь задана массовыми долями, то 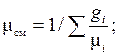
 кг/моль.
кг/моль.
Сделаем проверку полученных значений  , учитывая, что
, учитывая, что
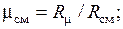
 кг/моль.
кг/моль.
5. Найдем парциальные давления компонентов через объемные доли:
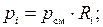
 (Па) = 12 (кПа);
(Па) = 12 (кПа);
 (кПа);
(кПа);
 (кПа);
(кПа);
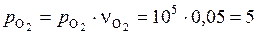 (кПа).
(кПа).
Парциальные давления компонентов, выраженные через массовые доли: 
 (кПа);
(кПа);
 (кПа);
(кПа);
 (кПа);
(кПа);
 (кПа).
(кПа).
Сделаем проверку:  ;
;
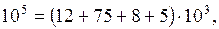

6. Найдем массу смеси: 
 (кг).
(кг).
7. Определим массовые доли компонентов через массовые доли:

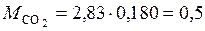 (кг);
(кг);
 (кг);
(кг);
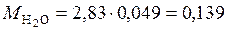 (кг);
(кг);
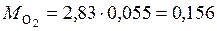 (кг).
(кг).
Сделаем проверку: 
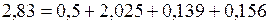 .
.
8. Рассчитаем парциальные объемы компонентов через объемные доли:
 (при
(при  и
и  ):
):
 (м3);
(м3);  (м3);
(м3);
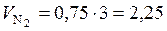 (м3);
(м3);  (м3).
(м3).
Сделаем проверку: 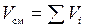 ;
;
 ;
;
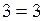 .
.
9. Вычислим парциальную плотность компонентов:
 (при
(при 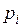 и
и  ):
):
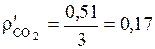 (кг/м3);
(кг/м3); 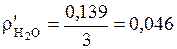 (кг/м3);
(кг/м3);
 (кг/м3);
(кг/м3); 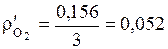 (кг/м3).
(кг/м3).
10. Найдем плотности компонентов при заданных условиях (при  и
и  ):
):  ;
;
 (кг/м3);
(кг/м3);  (кг/м3);
(кг/м3);
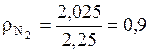 (кг/м3);
(кг/м3);  (кг/м3).
(кг/м3).
11. Плотность газовой смеси при заданных условиях (при  и
и  ):
):
– через объемные доли:
 ,
,
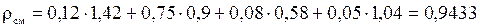 (кг/м3);
(кг/м3);
– через массовые доли:
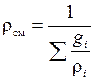 ,
,
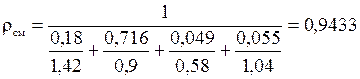 (кг/м3);
(кг/м3);
– через парциальные плотности компонентов:
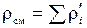 ;
;
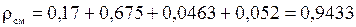 (кг/м3).
(кг/м3).
Сделаем проверку:
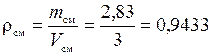 (кг/м3).
(кг/м3).
12. Найдем плотности компонентов при нормальных физических условиях (при  Па и
Па и  К):
К):
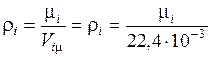 (кг/м3);
(кг/м3);
 (кг/м3);
(кг/м3); 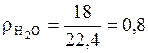 (кг/м3);
(кг/м3);
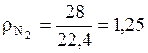 (кг/м3);
(кг/м3);  (кг/м3).
(кг/м3).
13. Найдем плотность смеси при нормальных условиях:
– через объемные доли:  ,
,
 (кг/м3);
(кг/м3);
– через массовые доли:
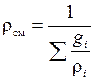 ,
,
 (кг/м3).
(кг/м3).
Сделаем проверку: 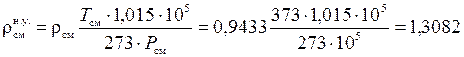 (кг/м3).
(кг/м3).
14. Находим теплоемкость смеси при  К:
К:
– молярную изобарную: 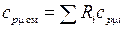 .
.
По табл. 1 Приложения 2 находим молярные изобарные теплоемкости компонентов:  (Дж/(кг·К);
(Дж/(кг·К);
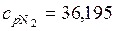 (Дж/(кг·К);
(Дж/(кг·К); 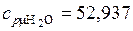 (Дж/(кг·К);
(Дж/(кг·К);
 (Дж/(кг·К);
(Дж/(кг·К);

 (Дж/кг·).
(Дж/кг·).
Молярную изохорную теплоемкость смеси найдем из уравнения Майера:
 ;
;
 Дж/(моль·К).
Дж/(моль·К).
Определим массовые теплоемкости:
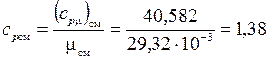 кДж/(кг·К);
кДж/(кг·К);
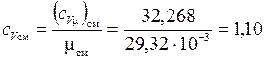 кДж/(кг·К).
кДж/(кг·К).
15. Находим среднюю теплоемкость смеси в диапазоне изменения температур от 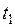 до
до 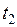 по формуле:
по формуле:
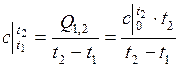 .
.
Значения средних теплоемкостей  выбираем по температуре
выбираем по температуре 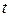 из табл. 1-5 Приложения 2.
из табл. 1-5 Приложения 2.
– Найдем среднюю мольную изобарную теплоемкость смеси в интервале температур от 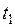 до
до 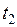 :
:
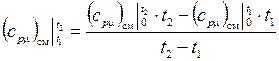 ,
,
где  ;
;
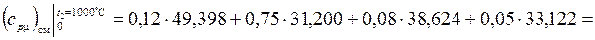

 Дж/(моль·К);
Дж/(моль·К); 
 Дж/(моль·К);
Дж/(моль·К);
 Дж/(моль·К).
Дж/(моль·К).
Найдем среднюю мольную изохорную теплоемкость, используя уравнение Майера:
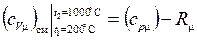 ;
;
 Дж/(моль·К).
Дж/(моль·К).
– Величину средней объемной теплоемкости определим по известной средней мольной теплоемкости и формуле:
 ;
;
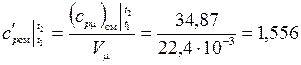 кДж/(м3·К);
кДж/(м3·К);
 кДж/(м3·К).
кДж/(м3·К).
– Найдем значение средней массовой теплоемкости смеси:
 кДж/(кг·К);
кДж/(кг·К);
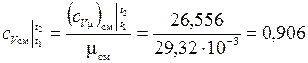 кДж/(кг·К).
кДж/(кг·К).
16. Найдем затраты тепла на нагревание при  :
:
– двух молей смеси ( моль):
моль):
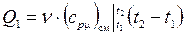 ;
;
 (кДж).
(кДж).
– 10 м3 смеси (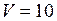 м3):
м3):
 ;
;
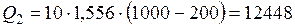 (кДж).
(кДж).
– 7 кг смеси ( кг):
кг):
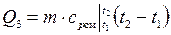 ;
;
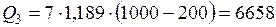 (кДж).
(кДж).
2. Процессы смешения
Решение большого количества технических задач часто сопряжено со смешением различных газов (жидкостей) или разных количеств одного и того же газа (жидкости), находящихся в различных термодинамических состояниях. Для организации процессов смещения разработан достаточно большой ряд самых разнообразных смесительных устройств и аппаратов.
При термодинамическом анализе процессов смешения обычно задача сводится к определению параметров состояния смеси по известным параметрам состояния исходных смешивающихся компонентов.
Решение этой задачи будет различным в зависимости от условий, при которых осуществляется этот процесс. Все способы образования смесей газов или жидкостей, происходящие в реальных условиях, можно разделить на три группы: 1) процесс смешения в постоянном объеме; 2) процесс смешения в потоке; 3) смешение при заполнении объема.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 292; Нарушение авторских прав?; Мы поможем в написании вашей работы!