
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
РЫБИНСК 2007 4 страница
|
|
|
|
Рассчитав параметры потоков после смешения можно проанализировать процесс с позиции второго начала термодинамики. Для этого необходимо вычислить энтропию, эксергию потоков до и после процесса смешения и потери эксергии после смешения. Удельные эксергии потока в различных сечениях рассчитываемых смесительных аппаратов и устройств могут быть найдены по зависимостям
 . (2.11)
. (2.11)
Эксергетический КПД процесса смешения определяется отношением эксергии газовой смеси к сумме эксергий смешивающихся компонентов
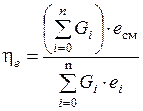 . (2.12)
. (2.12)
Суммарный поток потерь эксергии в процессе смешения может быть найден по известному значению суммарной эксергии смешивающихся потоков и численному значению эксергетического КПД
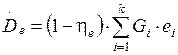 . (2.13)
. (2.13)
Если учитывать поэлементную необратимость процесса в различных сечениях аппарата смешения, то в случае расчета эжектора можно найти потери в сопловом устройстве смешивающего аппарата
 . (2.14)
. (2.14)
Тогда необратимость диффузора устройства может быть найдена как очевидная разность с учетом аддитивности как энтропии, так и эксергии
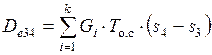 . (2.15)
. (2.15)
Однако наибольшую необратимость имеет непосредственно процесс смешения. Потери эксергии на смешении могут быть определены по известным параметрам до и после смешения.
Например для пароструйного эжектора, показанного на рисунке потери смешения, возникающие при смешении, находятся в соответствии с параметрами в характерных расчетных сечениях
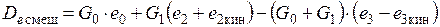 . (2.16)
. (2.16)
Поток эксергии на выходе из диффузора
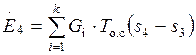 . (2.17)
. (2.17)
Проверка расчетов может быть выполнена на основании первого начала термодинамики. Сумма эксергии на входе в аппарат должна быть равна эксергии на выходе сложенной с суммарными потерями эксергии
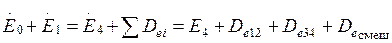 . (2.18)
. (2.18)
По рассчитанным значениям строится диаграмма потоков эксергии и анергии.
2.5. Индивидуальные задания по расчету
смешения потоков
Приведенные в настоящем разделе примеры задач на расчет процессов смешения потоков носят наиболее общий характер часто встречающихся элементов, требующих термодинамического обсчета в процессе создания промышленных устройств и сложной техники. В качестве примера в пособии приведен расчет пароструйного эжектора пароэжекторной установки. В авиационном двигателестроении можно привести пример смесителя двух контурного воздушно-реактивного двигателя, эжекторы, применяемые в системах кондиционирования и вентиляции, пароструйные и газоструйные насосы и т. д.
В предлагаемых для самостоятельного решения обычно заданы термо-газодинамические характеристики (параметры) смешивающихся потоков. Требуется определить параметры на выходе из устройства поэлементно в характерных сечениях (узлах), найти потери эксергии приращение энтропии. Определить суммарные потери и построить эксергетическую диаграмму. Сделать проверку осуществленного расчета по тождественности баланса эксергии. Сумма эксергии на входе должна быть равна сумме эксергии на выходе плюс сумма всех потерь эксергии по тракту аппарата
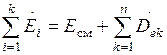 . (2.18)
. (2.18)
Погрешность баланса не должна превышать одного процента. Решение пароструйного эжектора вести с использованием табл. 7-8 Приложения водяного пара и 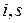 -диаграммы.
-диаграммы.
Для газовых смесей расчет можно вести с введением предположения об идеальности или с учетом их реальных свойств. Во втором случае необходимо использовать приведенные в Приложении 2 табл. значений термодинамических параметров для различных газов.
Приведем ряд индивидуальных заданий, наиболее часто встречающихся в инженерных проектировочных расчетах. При их выполнении во всех случаях рассчитать потоки и потери эксергии и построить эксергетическую диаграмму.
1. В канале смешиваются газы, поступающие из трех трубопроводов: 2 кг воздуха при p 1 = 200 кПа и T 1 = 500 К, 3 кг углекислого газа при p 2 = 200 кПа и T 2 = 400 К; 5 кг кислорода при p 3 = 300 кПа и T 3 = 300 К. При постоянных теплоемкостях определить температуру, удельный объем и энтропию смеси при давлении 100 кПа.
2. В сборном газоходе котельной смешиваются уходящие газы трех котлов, имеющие атмосферное давление. Для упрощения принимается, что эти газы имеют одинаковый состав, а именно: CO2 = 11,8 %; O2 = 6,8 %; N2 = 75,6 %; H2O = 5,8 %. Часовые расходы газов составляют: V 1 = 7100 м3/ч; V 2 = 2600 м3/ч; V 3 = 11200 м3/ч, а температуры газов соответственно равны: t 1 = 170 °C, t 2 = 220 °C, t 3 = 120 °C. Определить температуру, энтропию газов после смешения и их объемный расход через дымовую трубу при этой температуре.
3. Уходящие газы из трех паровых котлов при давлении 100 кПа смешиваются в сборном газоходе и через дымовую трубу удаляются в атмосферу. Объемный состав уходящих газов из отдельных котлов следующий:
из первого котла – CO2 = 10,4 %, O2 = 7,2 %, N2 = 77,0 %, H2O = 5,4 %
из второго котла – CO2 = 11,8 %, O2 = 6,9 %, N2 = 75,6 %, H2O = 5,8 %
из третьего котла – CO2 = 12,0 %, O2 = 4,1 %, N2 = 77,8 %, H2O = 6,1 %.
Часовые расходы газов составляют:
m1 = 12000 кг/ч, m2 = 6500 кг/ч, m3 = 8400 кг/ч, а температуры газов соответственно t 1 = 130 °C, t 2 = 180 °C, t 3 = 200 °C.
Определить температуру, массовый расход и энтропию уходящих газов после смешения в сборном газоходе.
4. В газоходе смешиваются три газовых потока, имеющих одинаковое давление, равное 200 кПа. Первый поток представляет собой азот с объемным расходом V 1 = 8200 м3/ч при t 1 = 200 °C, второй поток – двуокись углерода с V 2 = 7600 м3/ ч при t 2 = 500 °C и третий поток – воздух с V 3 = 6400 3/ч при t 3 = 800 °C. Определить температуру, энтропию и объемный расход газов после смешения в общем газопроводе.
5. Продукты сгорания из газохода парового котла в количестве 400 кг/ч при температуре 900 °C должны быть охлаждены до 500 °C и направлены в сушильную установку. Газы охлаждаются смешением газового потока с потоком воздуха при температуре 20 °C. Давление в обоих газовых потоках одинаково. Определить газовый расход воздуха, если известно, что R газ = R возд. Теплоемкость продуктов сгорания принять равной теплоемкости воздуха.
Вычислить массовый расход эжектирующего потока пара, потери эксергии в эжекторе и определить его эксергетический КПД при следующих данных.
2.6. Пример выполнения индивидуального задания
по расчету смешивающихся потоков
Для работающего на водяном паре пароэжекторного аппарата, в котором насыщенный пар с расходом G 0 = 1,00 кг/с сжимается от давления p 0 = 1,5 кПа (t 0 = 13,0 °C) до давления pm = 5 кПа, вычислим массовый расход G 1, эжектирующего потока пара. Последний имеет параметры p 1 = 0,3 МПа и t 1 = 150 °C. Необратимое расширение в сопле происходит при is ¢ = 0,90, необратимое сжатие в диффузоре – при iSD = 0,70 [4].
Решение.
Рассмотрим сначала идеальный случай обратимого пароструйного аппарата. В поперечных сечениях 0,1 и 4 пренебрегаем кинетической энергией по сравнению с термодинамической энтальпией потока вещества, т. е. положим W 0 = W 1 = W 4 = Wm = 0. Тогда для пароструйного аппарата справедливы два уравнения баланса энергии и энтропии в виде:
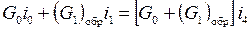 *
*
и
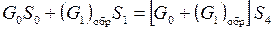 *.
*.
Для обратимого пароструйного аппарата состояние 4* на i, s -диаграмме определяется точкой пересечения прямой, соединяющей состояния 0, 1 с изобарой P = Pm (рис. 2.7). Из уравнений баланса получаем отношение массовых расходов
 .
.
Это двойное уравнение служит, во-первых, для определения состояния с использованием дополнительного условия i 4* = i (pm 1 S 4*) и, кроме того, для определения mобр. С помощью таблиц водяного пара [7-10] находим i 4* = 2576,9 кДж/кг и S4* = 8,4454 кДж/(кг×К). Отсюда получаем:
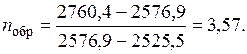
Если мы хотим получить то же конечное давление pm в реальном, необратимо работающем пароструйном аппарате, то необходимо подвести существенно больший массовый расход эжектирующего потока пара
G > (G)обр. Он расширяется в эжектирующем сопле до давления p 0 (конечное состояние 2 на рис. 2.7) и приобретает скорость:
 .
.
Для вычисления скорости W 3 после необратимого смешения с практически покоящимся паром низкого давления применим теорему импульсов к выделенному на рис. 2.6 объему, в котором происходит смешение. Изменение потока импульса равно результирующей k всех сил, действующих на границах смесительного объема:
 .
.
 Рис. 2.7. Изменение состояния водяного пара
в пароструйном аппарате
Рис. 2.7. Изменение состояния водяного пара
в пароструйном аппарате
|
Эти силы представляют собой силы давления в двух поперечных сечениях потока и касательные силы на стенках. Сделаем два упрощающих предположения: k = 0 и p 3 = p 0, которые точно никогда не выполняются. С учетом этих предположений и при W 0 = 0 из уравнения импульсов получаем:
G 0/ G 1 = W 2/ W 3 – 1. (2.3.)
Скорость W 3 должна иметь такую величину, чтобы смесь, вытекающая из диффузора в состоянии 4, приобрела на изобаре p = pm скорость
W 4» 0. Тогда должно выполняться условие:
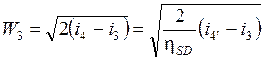 .
.
Подставляя теперь выражения для W 2 и W 3 в уравнение (2.3), получим:
 .
.
Можно еще (рис. 2.7) с хорошим приближением положить, что
i 4’ – i 3 = i 4* – i 3* ибо изобары p = p 0 и p = pm на i, S -диаграмме очень слабо расходятся. Кроме того, из i, S -диаграммы находим следующее соотношение:
 .
.
Отсюда окончательно получаем:
 .
.
При заданных значениях КПД находим:
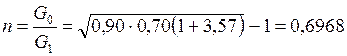 .
.
Таким образом, необходим расход эжектирующего пара
G 1 = 1,435 кг/с вместо (G 1)обр = 0,280 кг/с в идеальном случае обратимых процессов.
Вычислим потери эксергии в необратимо работающем пароструйном аппарате и определим его эксергетический КПД. Сделаем предположение, что эксергия водяного пара равна нулю при нормальных условиях окружающей среде: t о.с = 20 °С; p о.с = 0,1 МПа. Сопоставим сначала параметры состояния для различных сечений, эти данные приведены в табл. 2.2, где указаны величины i, S, e, удельная эксергия потока e = i – i о.с – T о.с(S – S о.с) и эксергия кинетической энергии e кин = W 2/2. Эти значения вычислены с использованием таблиц водяного пара и соотношений, указанных при рассмотрении примера.
Значения эксергии e 0, e 2 и e 3, соответствующие давлению p 0 = 1,5 Па, все отрицательны. Это означает, что покоящийся водяной пар в указанных состояниях не может произвести никакой полезной работы, если его с помощью какого-либо обратимого стационарного процесса течения перевести в состояние, соответствующее параметрам окружающей среды.
Таблица 2.2
| Состояние | i, кДж/кг | S, кДж/(кг×К) | W, м/с | e, кДж/кг | e кин, кДж/кг |
| О.С | 2525,5 2760,4 2097,7 2433,9 2664,0 84,0 | 8,8288 7,0771 7,3345 8,5093 8,7038 0,2963 | 678,3 | – 59,8 688,6 – 49,5 – 57,7 115,3 | 662,4 230,0 |
В таком процессе необходимо затратить большое количество работы, что приводит к еще более низкому давлению.
Потоки эксергии в различных сечениях пароструйного аппарата изображены схематически на рис. 2.8.
Суммарный поток эксергии, вводимой пароэжекторным аппаратом, равен сумме эксергий эжектирующего и эжектируемого потоков на входе в устройство
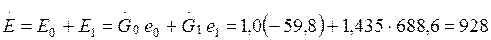 кВт.
кВт.
Эксергетический КПД аппарата определяется следующим образом:
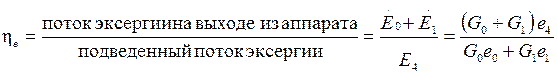 ,
,
откуда получаем
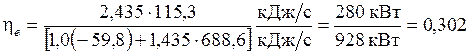 .
.
Почти 70 % подведенной эксергии теряется из-за необратимости процессов.
Суммарный поток потерь эксергии равен:
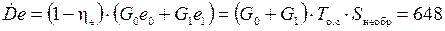 (кВт).
(кВт).
Из них теряется в сопле:
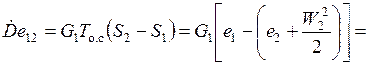
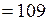 (кВт)
(кВт)
и в диффузоре
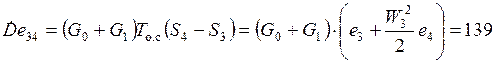 (кВт).
(кВт).
Но наибольшие потери эксергии возникают при смешении:
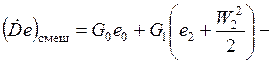
 (кВт).
(кВт).
 Рис. 2.8. Схема распределения
потоков эксергии
в пароструйном аппарате
Рис. 2.8. Схема распределения
потоков эксергии
в пароструйном аппарате
|
Проверка энергетического баланса по проведенному расчету дает удовлетворительное совпадение

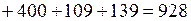 кВт.
кВт.
По полученным результатам в масштабе построим диаграмму потоков эксергии (рис. 2.8).
Таким образом, процессы в пароструйном аппарате имеют большую степень необратимости. Эти большие потери эксергии экономически можно оправдать лишь тем, что пароструйный аппарат имеет очень простую конструкцию (не содержит никаких движущихся частей) и что он представляет собой единственное устройство для сжатия среды, которое работает при очень малых давлениях и больших массовых расходах и может переработать большие объемные расходы необходимого рабочего тела табл.2.3.
Таблица 2.3
Результаты расчета смешения в потоке
| Номер варианта | Втекающий насыщенный пар | Эжектирующий пар | Давление сжатия pm, кПа | КПД сопла, h SS | КПД диффузора, h SD | |||
| G 0, кг/ с | p 0, кПа | t 0, °C | p 1, МПа | t 1, °C | ||||
| 1,7 | 0,3 | 0,9 | ||||||
| 1,1 | 0,8 | |||||||
| 2,3 | 1,6 | 0,8 | ||||||
| 3,6 | 0,9 | |||||||
| 1,0 | 0,2 | 0,9 | ||||||
| 2,0 | 17,5 | 0,5 | 0,8 |
Окончание табл. 2.3
| 2,5 | 0,8 | 0,8 | ||||||
| 24,1 | 0,9 | |||||||
| 3,5 | 26,7 | 0,5 | 0,8 | |||||
| 1,5 | 0,4 | 0,8 |
Построить диаграмму потоков эксергии и анергии (рис. 2.8).
 Рис. 2.9. Диаграмма потоков эксергии и анергии эжектора
Рис. 2.9. Диаграмма потоков эксергии и анергии эжектора
|
2.7. Смешение при заполнении объема
Задачи аналогичного типа часто встречаются на газозаправочных станциях при заполнении баллонов компремированным газом. Похожие процессы имеют место и на других машиностроительных и газоразделительных предприятиях.
При этом в емкостях, поступающих на заправку, практически всегда есть некоторое количество остаточной массы газа, находящейся в нем под давлением. Многие промышленные предприятия, научно-исследовательские лаборатории оснащены рампами с размещенными на них сосудами высокого давления, выполняющими роль аккумуляторных резервуаров для хранения сжатого воздуха. По мере его использования запасы сжатого воздуха восполняются. При этом реализуется все тот же процесс смешения при заполнении баллона, емкости, резервуара.
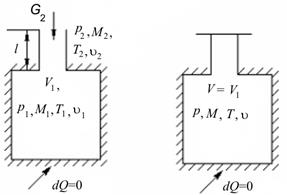 Рис. 2.10. Смешение при
заполнении объема
Рис. 2.10. Смешение при
заполнении объема
|
Пусть сосуд постоянного объема  требуется заполнить газом (жидкостью) до давления р. В сосуде находится газ с параметрами
требуется заполнить газом (жидкостью) до давления р. В сосуде находится газ с параметрами  , масса которого М 1. Газ (жидкость) с параметрами
, масса которого М 1. Газ (жидкость) с параметрами 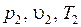 вводится в сосуд через трубопровод (рис. 2.10). Очевидно, что необходимо выполнение неравенства по давлению
вводится в сосуд через трубопровод (рис. 2.10). Очевидно, что необходимо выполнение неравенства по давлению
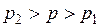 .
.
Процесс смешения протекает адиабатно. Чтобы поместить газ в сосуд необходимо совершить работу проталкивания, величина которой определяется очевидным соотношением
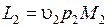 .
.
Эта работа в конечном итоге совершается над газом, находившемся в сосуде
 .
.
Но т. к. система адиабатна, то эта работа может быть совершена лишь за счет внутренней энергии системы
 .
.
Очевидно, что в соответствии с законом сохранения вещества 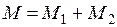 . Тогда после приравнивания правых частей выражений для расчета работы, получим
. Тогда после приравнивания правых частей выражений для расчета работы, получим
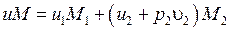
или
 ,
,
откуда
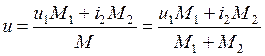 . (2.4)
. (2.4)
Удельный объем смеси
 . (2.5)
. (2.5)
Зная и и u, с помощью диаграмм состояния нетрудно определить остальные параметры (р, Т и S).
Для идеальных газов они могут быть определены аналитически.
 ,
, 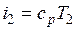 ,
, 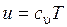 ,
, 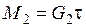 ,
,
где t – время натекания.
 , (2.6)
, (2.6)
где 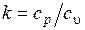 – показатель изоэнтропы идеального газа.
– показатель изоэнтропы идеального газа.
Давление газа после смешения
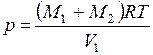 . (2.7)
. (2.7)
По Т и р находится S.
Если не пренебрегать кинетической энергий потока с массой 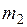 и модулем скорости
и модулем скорости 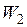 , подаваемую в резервуар при заполнении объема, то внутреннюю энергию конечной массы в объеме по завершению процесса заполнения можно рассчитать из уравнения баланса полной энергии
, подаваемую в резервуар при заполнении объема, то внутреннюю энергию конечной массы в объеме по завершению процесса заполнения можно рассчитать из уравнения баланса полной энергии
 , (2.8)
, (2.8)
где 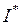 – энтальпия изоэнтропийно-заторможенного потока.
– энтальпия изоэнтропийно-заторможенного потока.
Перепишем последнее выражение через удельные величины и соответствующие массы
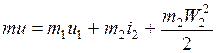 . (2.9)
. (2.9)
Считая газ идеальным, а его теплоемкость постоянной последнее уравнение перепишется в виде
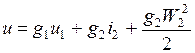 . (2.10)
. (2.10)
Выражение (2.10) с учетом 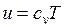 , а
, а 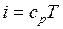 перепишется в виде
перепишется в виде
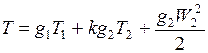 , (2.11)
, (2.11)
где 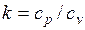 – отношение изобарной и изохорной теплоемкостей;
– отношение изобарной и изохорной теплоемкостей;
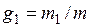 ;
; 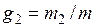 – массовые доли компонентов газа находящегося в баллоне до смешения и поступившего в баллон в процессе смещения.
– массовые доли компонентов газа находящегося в баллоне до смешения и поступившего в баллон в процессе смещения.
Для реального газа определив в процессе расчета давление 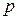 , внутреннюю энергию
, внутреннюю энергию 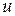 и удельный объем
и удельный объем  по таблицам термодинамических параметров газа Приложение 2 можно определить энтропию, плотность и другие недостающие параметры и произвести расчет энтропии так, как это рекомендуется, следуя методики расчета изложенной в главе «Газовые смеси» настоящего пособия.
по таблицам термодинамических параметров газа Приложение 2 можно определить энтропию, плотность и другие недостающие параметры и произвести расчет энтропии так, как это рекомендуется, следуя методики расчета изложенной в главе «Газовые смеси» настоящего пособия.
Процесс смешения существенно необратим и приращение энтропии при его осуществлении можно найти как разность энтропии смеси газа и суммы энтропий смешивающихся газов в состоянии до процесса смешения.
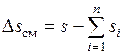 (2.12)
(2.12)
или через удельные энтропии и соответствующие массы смеси и исходных газов
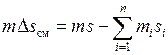 . (2.13)
. (2.13)
После деления на массу результирующей смеси зависимость (2.13) сводится к виду
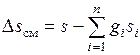 . (2.14)
. (2.14)
2.8. Индивидуальное задание на расчет процесса смешения при заполнении объема
Типичная задача может быть сформулирована следующим образом в резервуаре содержащем 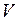 м3 находится некоторый известный газ при определенном давлении
м3 находится некоторый известный газ при определенном давлении 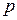 и температуре
и температуре 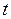 по трубопроводу в него подается в течении времени
по трубопроводу в него подается в течении времени 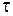 газ того же (или другого) химического состава с расходом
газ того же (или другого) химического состава с расходом 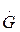 кг/с при давлении
кг/с при давлении  и температуре
и температуре 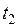 . Гидравлические потери отсутствуют. Считая газ идеальным определить параметры образовавшейся смеси, рассчитать энтропии и эксергию компонентов до смешения и газовой смеси, определить потери эксергии при смешении и построить эксергетическую диаграмму.
. Гидравлические потери отсутствуют. Считая газ идеальным определить параметры образовавшейся смеси, рассчитать энтропии и эксергию компонентов до смешения и газовой смеси, определить потери эксергии при смешении и построить эксергетическую диаграмму.
2.9. Пример выполнения индивидуального задания по расчету процесса смешения при заполнении объема
Условие задачи.
В резервуаре объемом 5 м3 находится кислород под давлением 300 кПа и температуре 47 °С. По трубопроводу в резервуар после открытия крана начинает поступать углекислый газ под давлением 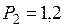 МПа и температуре
МПа и температуре  °С в течении 5 с с расходом 0,12 м3/с. Считая газ идеальным, рассчитать параметры газа после смешения. Найти приращение энтропии, потери эксергии и построить эксергетическую диаграмму. Скорость течения углекислого газа 10 м/с.
°С в течении 5 с с расходом 0,12 м3/с. Считая газ идеальным, рассчитать параметры газа после смешения. Найти приращение энтропии, потери эксергии и построить эксергетическую диаграмму. Скорость течения углекислого газа 10 м/с.
Дано:
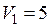 м3 м3
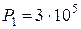 Па Па
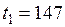 °С °С
 Па Па
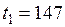 °С °С
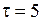 С С
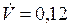 м3/с м3/с
 м/с м/с
|


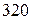 К К

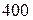 К К
|
Р, Т, 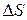 , , 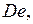 Е 1, Е 2, Е –? Е 1, Е 2, Е –?
|
Анализ.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 822; Нарушение авторских прав?; Мы поможем в написании вашей работы!