Процессы, приводящие к уменьшению энтропии, в изолированных или замкнутых системах невозможны

Если к термодинамической системе, состоящей из огромного числа частиц, подходить с позиции вероятностных законов, то представляется очевидным, что любой самопроизвольный процесс протекает в направлении, при котором система переходит из менее вероятного в более вероятное состояние.

Этот вывод может служить одной из формулировок второго начала термодинамики.

Покажем, что статистическая формула Больцмана S = R ×ln W, которая выражает энтропию через вероятность термодинамического состояния W,действительно соответствует определению энтропии через приведенную (т.е. деленную на температуру) теплоту d Q / T. Доказательство выполним для модели идеального газа, начав с вычисления теплоты, приобретенной системой при обратимом изотермическом (Δ U = 0, см. далее) расширении 1 моля идеального газа.

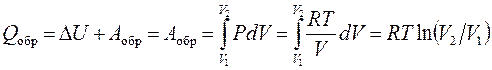. (3.4)

Очевидно, что чем больше объем V, тем больше вероятность нахождения в нем рассматриваемого моля газа. Заменяя отношение V ₂/ V ₁ равным ему W ₂/ W ₁ и сопоставляя деленное на Т соотношение (3.4) с вытекающим из формулы Больцмана изменением энтропии

D S = S ₂ – S ₁ = R ×ln(W ₂/ W ₁), получаем D S = Q _обр/ T, которое соответствует определению (3.3).

Далее, не сложно показать, что найденная работа обратимого изотермического расширения (3.4) всегда больше работы соответствующего необратимого процесса

А _необр = P (V ₂ – V ₁) = RT (V ₂ – V ₁)/ V ₂ = RT (1 – V ₁/ V ₂), (3.5)

когда отпущенный при объёме V ₁ поршень первоначально сжатого в цилиндре газа в условиях постоянного внешнего давления P (возможно после нескольких колебаний) остановится в положении с объёмом V ₂. Неравенство вычисленных работ А _обр > А _необр для рассмотренного идеального газа в изотермическом (Δ U = 0) процессе с учетом первого закона термодинамики приводит к неравенству Q _обр > Q _необр. Его деление на T дает неравенство Δ S > Q _необр / T, (3.6)

которое обосновывает принципиальную часть второго начала термодинамики (3.3').

Второе начало термодинамики исключает возможность создания вечного двигателя второго рода, т.е. устройства, в котором при помощи кругового процесса охлаждается источник тепла, причем все количество теплоты превращается в механическую работу. Возможно лишь частичное превращение теплоты в работу (в противоположность обратному процессу).

Коэффициент полезного действия процесса, в котором происходит превращение теплоты в работу: 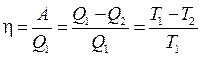. (3.7)

Q ₁и Q ₂ – количества теплоты отданное нагревателем и поглощенное холодильником, находящимся, соответственно, при температуре Т ₁и Т ₂. Второе равенство в (3.7) справедливо для полностью обратимых процессов (например, для цикла Карно).

Все естественные процессы (например, в тепловых машинах) протекают с меньшим коэффициентом полезного действия.

Дифференциальная форма соотношения (3.6) после подстановки в него (3.2) объединяет 1-ое и 2-ое начала термодинамики: TdS > dU + PdV + δ A _необр. При этом в совершаемой системой общей работе по всем ее видам выделена работа расширения PdV. В окончательной форме основного термодинамического соотношения

TdS ≥ dU + PdV + δ A (3.8)

знак равенства относится к обратимым процессам, а знак неравенства - к необратимым.

В изолированной системе (dU = 0, dV = 0,δ A= 0), т. е. при фиксированных U и V, как следует из (3.8), могут протекать процессы только с возрастанием энтропии: (dS) _U,V ≥ 0 (3.9)

В результате такого самопроизвольного процесса при рассматриваемых условиях (U, V = const) система приходит в состояние равновесия, а её энтропия достигает максимального значения. Соответствующие критерии равновесия в математической форме имеют вид:

(dS) _U,V = 0, (d ² S) _U,V < 0. (3.10)

3. 2. Характеристические функции

Совершаемая системой работа А, при её выражении из основного термодинамического соотношения (3.8)

δ A ≤ TdS - dU - PdV (3.11)

будет максимальной при обратимом процессе (знак равенства в (3.11)). Например, максимальную полезную работу в химической реакции можно получить, если проводить её в обратимом гальваническом элементе.

Величина полезной работы будет зависеть от условий протекания реакции.

3.2.1. В самопроизвольном процессе при условии постоянства S, V (dS =0, dV =0),согласно (3.11), δ A ≤ - (dU) _{S , V}. Максимальная полезная работа равна убыли внутренней энергии системы U:

(A _обр) _{S , V} = - (Δ U) _{S , V} = - (U ₂ – U ₁) _{S , V} (3.12)

Внутренняя энергия как характеристическая функция объема V и непосредственно не измеряемой энтропии S не удобна и редко используется в термодинамике для решения практических задач.

3.2.2. Для самопроизвольного процесса при постоянных S, Р из (3.11) следует

δ A ≤ (- dU - PdV) _{S , Р} = − (dU + PdV) _{S , Р} = − (dН) _{S , Р}. (3.13)

Максимальная полезная работа при данных условиях равна убыли энтальпии системы Н = U + PV.

3.2.3. Для самопроизвольного процесса при постоянных Р и Т соотношение (3.11) можно представить в виде

δ A ≤ − d (U + PV − TS) _{T , Р} , (3.14)

поскольку дифференциал в последнем выражении при постоянных Р и Т действительно соответствует (3.11). Функция

G = U + PV – TS = H – TS (3.15)

называется термодинамическим потенциалом Гиббса или энергией Гиббса. Для обратимого процесса при постоянных Р и Т максимальная полезная работа равна убыли этой важнейшей для химии термодинамической функции состояния.

3.3. Критерии возможности и направленности самопроизвольного процесса и условия равновесия

Если направленность самопроизвольного процесса в изолированной системе определяется возрастанием энтропии (3.9), а равновесие – условиями её максимума (3.10), то для закрытых систем ответы на эти вопросы получают на основании величины полезной работы А > 0.

Максимальная полезная работа при задаваемых условиях постоянства параметров процесса (нижние индексы) определяется убылью соответствующей функции состояния или соответствующего термодинамического потенциала:

δ A = - (dU) _{S , V} , δ A = - (dH) _{S , P} , δ A = - (dF) _{T , V} , δ A = - (dG) _{T , P} . (3.16)

Т. о. при самопроизвольном протекании физико-химического или химического процесса в закрытой системе соответствующие условиям процесса термодинамические потенциалы должны уменьшаться, достигая в равновесии минимальных величин, удовлетворяющих критериям равновесия:

(dU) _{S , V} = 0, (dH) _{S , P} = 0, (dF) _{T , V} = 0, (dG) _{T , P} = 0; (3.17)

(d ² U) _{S , V} > 0, (d ² H) _{S , P} >0, (d ² F) _{T , V} >0, (d ² G) _{T , P} >0. (3.18)

К ранее введенным добавлен изохорно-изотермический потенциал (энергия Гельмгольца) F = U – TS. Поскольку большинство процессов в закрытых системах совершаются при постоянных Т и Р, то наиболее важны и используемы на практике соотношения для энергии Гиббса.

3.4. Основные термодинамические функции индивидуальных веществ

Количество тепла, принимаемое молем вещества, при повышении его температуры на 1 градус, называется его мольной теплоемкостью, соответственно при постоянном объеме или при постоянном давлении

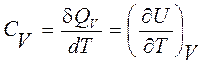, . (3.19)

Непосредственное использование 1-го начала термодинамики в форме (3.2') показывает, что C_V связана с изменением внутренней энергии. Дифференциал энтальпии Н = U + P · V при постоянном давлении (dH)_Р = dU + P · dV = (δ Q) _Р сопоставленный с (3.2') показывает, что C_Р взаимосвязана с изменением энтальпии.

Вытекающая из последнего соотношения взаимосвязь мольных теплоемкостей при постоянном давлении и постоянном объеме для газов (верхняя строка в (3.20)) легко устанавливается с использованием мольного уравнения Менделеева-Клапейрона.

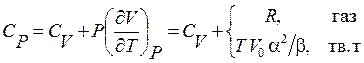(3.20)

Для твердых тел (нижняя строка) эта взаимосвязь выражается через молярный объем при 0 К (V ₀), изобарический коэффициент термического расширения (α) и изотермический коэффициент сжимаемости твердого тела (β).

Энтальпия нагревания вещества при изменении температуры от Т ₁ до Т ₂ − результат интегрирования C_Р (3.19):

. (3.21)

Температурное изменение энтропии при постоянном давлении следует из исходных определений энтропии (3.3) и теплоемкости C_Р:

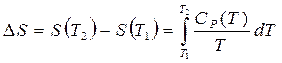. (3.21')

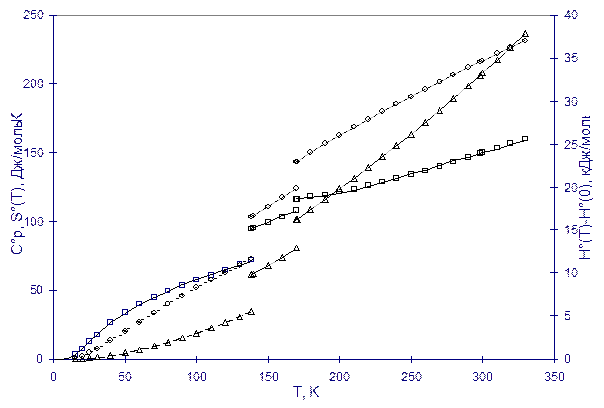
На рисунке приведен результат калориметрических измерений теплоемкости (квадратики) циклогексена - исходной функции для расчета энтальпии (кружочки) и энтропии (треугольники).

Термохимия (термодинамический раздел химии), кроме теплоемкости, занимается определением температур T_k и теплот 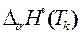фазовых и полиморфных превращений.

При наличии такой информации основные (наиболее используемые) термодинамические функции рассчитываются по формулам

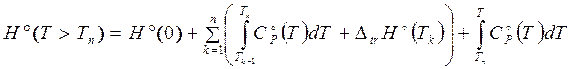, (3.23)

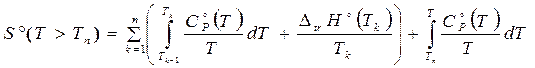. (3.24)

Дополненные стандартными энтальпиями образования (см. далее) они составляют основу термодинамических банков данных.

3.5. Термодинамические функции реакций

Предваряя анализ тепловых эффектов химических реакций, ещё раз остановимся насимвольном уравнении химической реакции

ν'₁ A₁ + ν'₂ A₂ = ν₃ A₃ + ν₄ A₄. (3H₂ + N₂ = 2NH₃) (3.25')

Δ n ₁ = − ν'₁·ξ, Δ n ₂ = − ν'₂·ξ, Δ n ₃ = +ν₃·ξ, Δ n ₄ = +ν₄ ξ. (3.26')

Реагенты в уравнении реакции, естественно, со сменой знака перенесём в правую часть

0 = ν₁ A₁ + ν₂ A₂ + ν₃ A₃ + ν₄ A₄. (0 = −3H₂ −N₂ + 2NH₃).

Стехиометрические коэффициенты для реагентов при этом следует считать отрицательными: (ν₁ = -ν'₁, ν₂ = - ν'₂). Компактное и математически изящное уравнение химической реакции из произвольного числа компонентов принимает вид:

0 = Σν _i A _i, ν _i < 0 для реагентов. (3.25)

Все текущие, в том числе и конечные количества реагентов и продуктов реакции единообразно выражаются через реакционную переменную ξ,:

Δ n_i = ν _i ξ, n_i = n _{0 i} + ν _i ξ. (3.26)

Изменение числа молей при протекании реакции пропорционально стехиометрическому коэффициенту – закон кратных отношений.

Если реакция происходит при постоянном объеме V, то указанный закон будет действовать и для концентраций (C_i = n_i /(V, л)) − молярности). Разделив (3.26) на V получим

Δ С_i = ν _i ξ', С_i = С _{0 i} + ν _i ξ', где ξ' = ξ/ V (3.26')

Закон сохранения массы для реакции (3.25) с использованием соотношений (3.26) 0 = ΣΔ m_i = Σ(M_i Δ n_i) = ξ Σ(M_i ν _i) сводится к равной нулю стехиометрической сумме мольных масс M_i: Σ M_i ν _i = 0.

Реакции синтеза аммиака 3H₂ + N₂ = 2NH₃ соответствует менее привычная для химиков _{(1) (2) (3)}

форма (3.25): 0 = −3H₂ − N₂ + 2NH₃. Убывающим по реакции веществам соответствуют отрицательные стехиометрические коэффициенты, а прибывающим – положительные. В частности, исходному «стехиометрическому» составу n ₀₁ =3 моль, n ₀₂ =1 моль, n ₀₃ =0 моль при «полном, 100%-ном» завершении реакции соответствует ξ = 1 моль(последняя строка нижеследующей таблички).

Таблица. Три задачки

1	2	3		1	2	3
(3.26): n 0 i = ni - νi ξ	ξ=(ni - n 0 i)/ νi	(3.26): ni = n 0 i + νi ξ
			(0-1)/(-1)=1	5-3*1=2		10+2*1=12
4+3*2=10	4+2=6		(4-0)/2=2
			(2-0)/2=1	3-3*1=0	1-1=0

Дата добавления: 2015-05-09