Исходные данные выделены жирным шрифтом

Изменение химического и фазового состава системы при протекании реакции влечет за собой изменение ее термодинамических характеристик и свойств.

Текущее изменение энтальпии

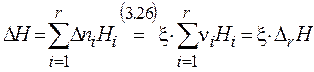(3.27) 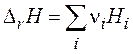(3.28)

выражается через стехиометрически определенную энергетическую характеристику реакции – энтальпию реакции D _r H.

При определении энтальпии химического соединения H_i необходимо выбрать уровень ее отсчета. Для этой цели используется функция

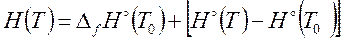, (3.29)

которая в теплотехнической литературе получила название полной энтальпии. Кроме энтальпии нагревания от T ₀ до T (в квадратных скобках) она выражена через энтальпию образования химического соединения из простых веществ при T ₀.

Комиссия ИЮПАК по термодинамике определила (1975 г.) в качестве основного стандартного состояния для газообразных веществ простое вещество в состоянии идеального газа с давлением Р º = 1 атм при любой фиксированной температуре. Для твердых и жидких веществ основное стандартное состояние – это состояние чистого вещества, находящееся под давлением Р º = 1 атм. Если специально не оговорено, принято T ₀ = 298,15 К.

Все стандартные значения отмечаются маленьким кружочком в позиции верхнего индекса с указанием температуры в скобках.

Стандартная энтальпия реакции общего вида 0 = Σν _i A _i из формул (3.28), (3.29) выражается через стандартные энтальпии образования реагентов и продуктов 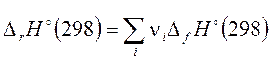. (3.30)

Пример: CH₄ + CO₂ = 2 CO + 2 H₂.

D _rH °(298) = -(-74,85) - (-393,51) + 2×(-110,5) + 2×(0) = 247,36 кДж/моль

В свою очередь, D _fH °(298) химического соединения – это D _rH °(298)образования моля этого соединения из простых веществ.

Например:

C, графит + 1/2 O₂ = CO, D _fH °(298) = –110,54 кДж/моль

H₂ + 1/2 O₂ = H₂O, ж D _fH °(298, ж) = –285,84 КДж/моль

3.5.1. Зависимость теплового эффекта реакции от температуры

можно получить, если формулу (3.29) с T ₀ = 298,15 К подставить в формулу (3.28):

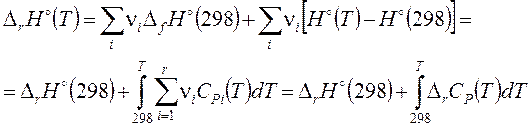
(3.31)

Дифференциальная форма температурной зависимости энтальпии реакции носит название уравнения Кирхгоффа

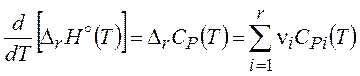. (3.32)

Если в данном температурном интервале D _rC_Р > 0, то при повышении температуры энтальпия возрастает, и наоборот.

Ранее определив другую важнейшую функцию – энтропию, мы уже привели формулу (3.24), которая определяет стандартное ее значение по данным о теплоемкости и энтальпиям D _trH ° фазовых и полиморфных превращений.

Заменив букву H буквой S вместо формул (3.27) и (3.28) для энтальпии получаем пропорциональное координате реакции изменение энтропии системы, выраженное через энтропию реакции .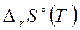

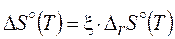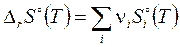, , (3.28')

В отличие от энергетических функций, 3-й закон термодинамики однозначно определяет нулевой уровень отсчета энтропии для каждого «нормального» вещества при 0 К.

Наконец, стандартные энтальпия и энтропия составляют стандартную энергию Гиббса реакции – её важнейшую термодинамическую характеристику: D _rG ° = D _rH ° – T D _rS °. (3.33)

3.6. Энтропия идеального газа и идеальной газовой смеси.

Подставив дифференциал мольного объема 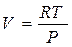идеального газа 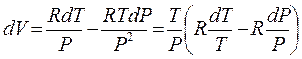в основное термодинамическое соотношение TdS = C_V dT + РdV и использовав связь (3.20) C_V = C_P – R получаем . Интегрирование от T ₁ и P ₁ до Т и Р даёт .

Энтропийная постоянная идеального газа S′ при конкретизированных T ₁ = 1 К, P ₁ = P ° = 101325 Па = 1 атм – это энтропия 1 моля газа при стандартном давлении P ° и температуре 1 К может быть вычислена методами статистической термодинамики по молекулярным постоянным. Т. о. абсолютная энтропия моля идеального газа

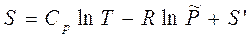, (3.35)

где стоящие под знаком ln T = T /1К и 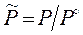- безразмерные величины.

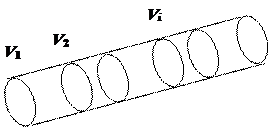
В стеклянный цилиндр, разделенный перегородками, поместим по ni молей разных газов. P и T во всех отсеках одинаковы.

S _{(до смешения)} = (3.36)

После разрушения перегородок и необратимого (диффузионного) смешения каждый из газов займет весь объем. При этом температура останется неизменной, поскольку внутренняя энергия газа не зависит от объема. Одинаковое и равное давление P после разрушения перегородок становится общим давлением 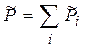, которое по закону Дальтона складывается из парциальных 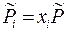, где 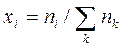- мольная доля i- гокомпонента в смеси.

Энтропия системы после смешения газов равна

S _{(после смешения)} = . (3.37)

Изменение энтропии в результате смешения газов называют энтропией смешения D S _см = S _{(после смешения)} – S _{(до смешения)}:

D S _см = 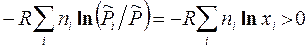. (3.38)

Оказывается, что это выражение определяет энтропию смешения не только газовых, но и жидких и твердых идеальных растворов. При смешении компонентов энтропия системы необратимо возрастает.

3.7. Энергия Гиббса смеси. Химический потенциал компонента

в растворе

Определение основных понятий химической термодинамики и получение общих соотношений продолжим на примере идеально газовой системы.

Энтальпию i -го компонента при (необязательном) условии постоянства C_p легко получить из её определения (3.19):

H_i = C_Рi × T + H _{0 i}, (3.39)

где H _{0 i} = U _{0 i} – внутренняя энергия моля идеального газа при 0 К.

Составим из 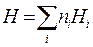и S (3.37) энергию Гиббса G = H – TS = 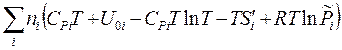. Объединив все слагаемые , которые зависят от природы i ‑го вещества и температуры, но не зависят от состава смеси, получаем

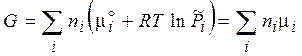, (3.40) 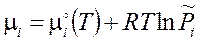. (3.41)

Величина μ _i называется химическим потенциалом i‑го компонента в газовой смеси. 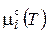- стандартный химический потенциал компонента при парциальном давлении .

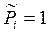Используя определение парциального давления , из (3.41) получаем другую форму химического потенциала 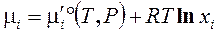(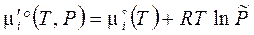), (3.41')

которую можно применять уже не только к газовым, но и к конденсированным смесям.

При протекании химических процессов происходит изменение состава реакционной смеси. Соответствующее изменение G:

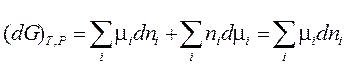, (3.42)

Можно показать, что 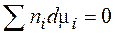, а из (3.42) следует фундаментальное определение химического потенциала 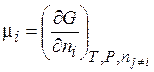(3.41'').

Являясь важнейшей характеристикой вещества в растворе, химический потенциал i‑го вещества - это, прежде всего, частная производная от энергии Гиббса по его мольному количеству в растворе.

3.8. Термодинамический закон действующих масс (ТЗДМ)

Для химической реакции общего вида 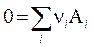(для реагентов n _i < 0) изменению состава компонентов при постоянных Т и Р, согласно (3.42), соответствует дифференциальное, а затем и конечное изменение энергии Гиббса.

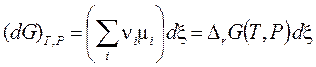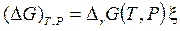, . (3.43)

По химическим потенциалам и стехиометрическим коэффициентам ν _i компонентов, аналогично энтальпии (3.28) и энтропии (3.28'), определена энергия Гиббса реакции

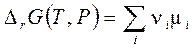. (3.44)

Равновесие в изобарно-изотермическом процессе, в соответствии условием (3.17), определяется нулевой скоростью изменения энергии Гиббса (3.43) в точке её минимума:

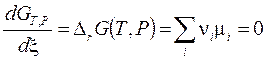. (3.45)

Это общее условие равновесия конкретизируем для газофазной реакции, подставив в него химические потенциалы (3.41) участников:

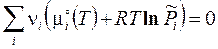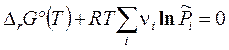, , (3.45')

где 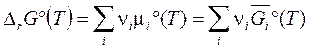(3.44')

- стандартная энергия Гиббса реакции.

Преобразование и эспоненцирование (3.45') приводит к уравнению:

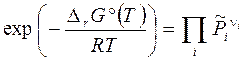(3.46)

Не зависящая от состава реакционной смеси его левая часть называется стандартной константой равновесия:

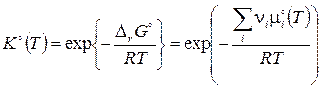. (3.47)

Правую часть (3.46) назовем стехиометрическим произведением концентраций. В данном случае оно выражено через равновесные значения безразмерных парциальных давлений.

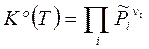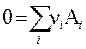(, ν _i < 0 для реагентов). (3.49)

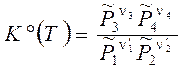(n'₁A₁+ n'₂A₂ = n₃A₃ + n₄A₄). (3.49')

Уравнение, отражающее условие равновесия химической реакции, называется термодинамическим законом действующих масс (ТЗДМ). Форма (3.49) - для реакции общего вида, (3.49') - для 4-х компонентного уравнения реакции в обычной записи.

Поскольку состав системы можно характеризовать разными концентрационными единицами, то различные, в общем случае размерные правые части ТЗДМ, слева должны уравниваться соответствующими константами равновесия. Подстановка связи 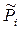с соответствующей концентрацией в (3.49) позволяет для каждой формы ТЗДМ выразить соответствующую константу равновесия через стандартную К° (Т).

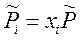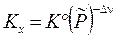, , ; (3.50 ^х)

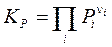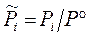, , ; (3.50 ^Р)

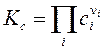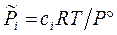, , . (3.50 ^с)

Здесь Dn = Sn _i = n₃ + n₄ – n'₁ – n'₂ – изменение числа молей в реакции, K_x, K_P, K_c – константы равновесия, соответствующие использованию мольных долей x_i, парциальных давлений P_i (атм) и концентраций c_i (моль/м³).

3.9. Направление протекания химической реакции. Использование термодинамического закона действующих масс для расчета состава равновесной смеси

Относительные парциальные давления компонентов реакции до момента их взаимодействия, т.е. в исходном состоянии, отметим дополнительным нижним индексом «0» и выразим энергию Гиббса реакции (3.44) из ТЗДМ (3.45'):

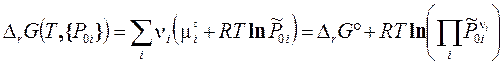(3.51)

Выражение (3.51) впервые получено Вант-Гоффом, а Де-Донде, исходя из необходимого для самопроизвольного протекания процесса отрицательного значения 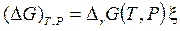(см. формулу (3.43) в разделе 3.3) сформулировал:

· Если в исходном состоянии энергия Гиббса реакции:

o < 0, то x > 0 и реакция потечет слева направо.

o > 0, то x < 0 и реакция потечет справа налево.

· Текущие концентрации будут изменяться до достижения своих равновесных значений при 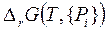= 0.

Расчет равновесного состава при фиксированных Т и Р и при заданной или вычисляемой по энергиям Гиббса веществ константе равновесия сводится к нахождению химической координаты реакции x. Для нескольких реакций вместо одного требуется решать уже систему уравнений ТЗДМ с привлечением специализированных компьютерных средств.

Ниже представлено решение для простых, но практически важных реакций. Форма ТЗДМ (3.50 ^х) соответствует мольным долям x_i.

Пример 1. Зависимость выхода йодистого водорода от соотношения реагентов.

	H2	+ J2	= 2 HJ	Dn = 0, Kx = K ° = 45,7 (Т = 718 К)
n 0 i :	m	n
ni = n 0 i + n i ×x:	m –x	n –x	2x	Σ ni = m + n

x_i = n_i / Σ n_i; ; .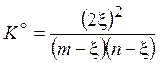

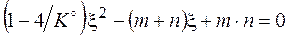Для удобства введены обозначения: 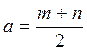, , A= 1−4/ K.^◦ Тогда

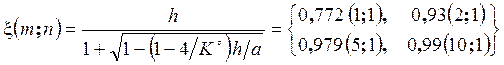
Результаты вычислений при различных исходных количествах йода и водорода (n; m) показывают, что выход по йоду x/ n можно повысить за счет избытка водорода!

Пример 2. Расчет выхода аммиака и его зависимость от давления.

		3 H2	+ N2	= 2 NH3	Dn = -2, Kx = K °(P, атм)^2, K °= 4,21∙10^-5 при Т = 720 К
n 0 i = n' i:
	ni = n 0 i + n i ×x:	3–3x	1–x	2x	S ni= 2(2-x)
	xi = ni /S ni: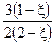

,

.

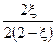
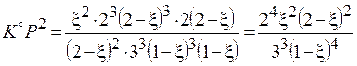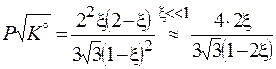
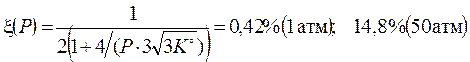Приемлемый выход можно достичь только при повышенных давлениях. На практике аммиак с 30 % -м выходом синтезируют при давлениях около 300 атм.

3.10. Влияние температуры и давления на химическое равновесие

Зависимость константы равновесия от давления явным образом выражена для 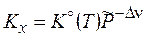в (3.50 ^x). Логарифмирование и дифференцирование по давлению дает:

. (3.52)

Последнее равенство в (3.52) получено из уравнения Менделеева-Клапейрона.

Анализ уравнения (3.52) показывает, что с увеличением общего давления реакционной смеси:

1) для реакций, сопровождающихся уменьшением числа молей и газового объема (Dn < 0 и D _rV < 0) K_x возрастает, а равновесие смещается вправо, в сторону образования продуктов;

2) в противном случае (Dn > 0 и D _rV > 0) – равновесие смещается влево, что делает реакцию менее выгодной.

Влияние температуры на химическое равновесие вытекает из зависимости логарифма стандартной константы равновесия (3.47) 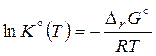от температуры:

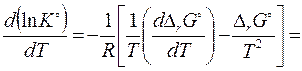
(3.53)

При выводе изобары (P = const) реакции Вант-Гоффа были использованы соотношения: G = H – TS и 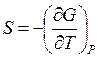в применении к реакции.

С увеличением температуры процесса, согласно (3.53):

1) для эндотермических (теплопоглощающих, D _rH ° > 0) реакций при положительной производной K ° будет возрастать, а равновесие сдвигается вправо, в сторону целевых продуктов;

2) для экзотермических (тепловыделяющих, D _rH ° < 0) реакций равновесие сдвигается влево, в сторону исходных веществ.

Математически установленные количественные закономерности о влиянии T и P на качественном уровне могут быть интерпретированы на основании принципа смещения равновесия Ле Шателье (- Брауна).

При нарушающем равновесие внешнем воздействии система переходит в такое состояние, при котором эффект этого воздействия ослабевает.

Например, повышение температуры для эндотермической (теплопоглощающей) реакции смещает равновесие в сторону увеличения выхода её продуктов, а для экзотермической – в сторону регентов.

Повышение давления смещает равновесие в сторону уменьшения объема, что нивелирует рост давления.

Наконец, добавление реагента смещает равновесие в сторону, уменьшающую добавок.

3.11. Химическое равновесие в гетерогенных системах.

Химические реакции, компоненты которых находятся в разных фазах, называются гетерогенными. Общая форма записи системы одновременно протекающих реакций химических реакций:

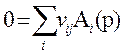, j – номер реакции, p – указатель фазы i- го компонента.

Рассмотрим две реакции, которые занумерованы римскими цифрами. Компоненты отмечены арабскими цифрами сверху; (тв) и (г) - указатели твердой и газовой фаз. Ниже, под каждым компонентом записаны их химические потенциалы. Газообразным компонентам соответствует форма (3.41), а твердым форма (3.41'). x ₁ = 1 соответствует индивидуальному тв. веществу.

_{1 2 3 4}

I. С(тв) + СО₂(г) = 2 СО(г), II. С(тв) = С(г)

,

,

.

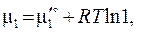
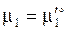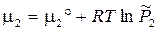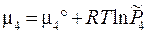
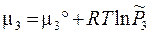Повторение вывода ТЗДМ (3.46) для конкретных уравнений I и II даёт:

, .

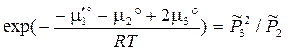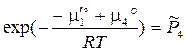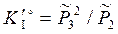, . (3.54)

Стандартные константы равновесия гетерогенных реакций содержат химические потенциалы всех компонентов. Стехиометрическое произведение концентраций образовано только газообразными компонентами.

Равновесный состав находится решением двух уравнений (3.54) с предварительным расчетом констант равновесия по данным 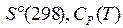для каждого вещества.

Отметим, что второе уравнение (3.54) отражает только фазовое равновесие между твердым и газообразным углеродом.

Дата добавления: 2015-05-09