Первое начало термодинамики. Внутренняя энергия системы

Внутренняя энергия системы

Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Так, например, при определении внутренней энергии некоторой массы газа не должна учитываться энергия движения газа вместе с сосудом и энергия, обусловленная нахождением газа в поле сил земного тяготения.

Следовательно, в понятие внутренней энергии включаются кинетическая энергия хаотического движения молекул, потенциальная энергия взаимодействия между молекулами и внутримолекулярная энергия[5].

Внутренняя энергия системы тел равна сумме внутренних энергий каждого из тел в отдельности и энергии взаимодействия между телами, представляющей собой энергию межмолекулярного взаимодействия в тонком слое на границе между телами. Последняя энергия столь мала по сравнению с энергией макроскопических тел, что ею можно пренебречь и считать внутреннюю энергию системы макроскопических тел равной сумме внутренних энергий образующих систему тел. Таким образом, внутренняя энергия является аддитивной величиной.

Внутренняя энергия является функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет всегда равно разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершался переход, т. е. независимо от процесса или совокупности процессов, приведших к переходу системы из одного состояния в другое.

Внутренняя энергия может изменяться за счет в основном двух различных процессов: совершения над телом работы A ′ и сообщения ему тепла Q. Совершение работы сопровождается перемещением внешних сил, воздействующих на систему. Так, например, при вдвигании поршня, закрывающего сосуд с газом, поршень, перемещаясь, совершает над газом работу A ′. По третьему закону Ньютона газ при этом совершает над поршнем работу .

Сообщение газу тепла не связано с перемещением внешних сил и, следовательно, не связано с совершением над газом макроскопической (т. е. относящейся ко всей совокупности молекул, из которых состоит тело) работы. В этом случае изменение внутренней энергии обусловлено тем, что отдельные молекулы более нагретого тела совершают работу над отдельными молекулами тела нагретого меньше. Передача энергии происходит при этом также через излучение. Совокупность микроскопических (т. е. захватывающих не все тело, а отдельные его молекулы) процессов, приводящих к передаче энергии от тела к телу, носит название теплопередачи.

Подобно тому, как количество энергии, переданное одним телом другому, определяется работой A, совершаемой друг над другом телами, количество энергии, переданное от тела к телу путем теплопередачи, определяется количеством теплоты Q, отданной одним телом другому. Таким образом, приращение внутренней энергии системы должно быть равно сумме совершенной над системой работы A ′ и количества сообщенного системе тепла Q

. (1.6)

Здесь U ₁ и U ₂ – начальное и конечное значение внутренней энергии системы. Обычно вместо работы A ′, совершаемой внешними телами над системой, рассматривают работу A (равную ), совершаемую системой над внешними телами. Подставив вместо A ′ и разрешив уравнение (1.6) относительно Q, получим

. (1.7)

Уравнение (1.7) выражает закон сохранения энергии и представляет собой содержание первого закона (начала) термодинамики. Словами его можно выразить следующим образом: количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

Сказанное отнюдь не означает, что всегда при сообщении тепла внутренняя энергия системы возрастает. Может случиться, что, несмотря на сообщение системе тепла, ее энергия не возрастает, а убывает (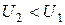). В этом случае, согласно (1.7), 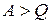, т. е. система совершает работу как за счет получаемой теплоты Q, так и за счет запаса внутренней энергии, убыль которой равна . Нужно также иметь в виду, что величины A и Q в (1.7) являются алгебраическими ( означает, что система в действительности не получает тепло, а отдает).

Из (1.7) следует, что количество теплоты Q можно измерять в тех же единицах, что и работу или энергию. В СИ единицей количества теплоты служит джоуль.

Для измерения количества теплоты применяется также особая единица, называемая калорией. Одна калория равна количеству теплоты, необходимой для нагревания 1 г воды от 19,5 до 20,5°C. Тысяча калорий называется большой калорией или килокалорией.

Опытным путем установлено, что одна калория эквивалентна 4,18 Дж. Следовательно, один джоуль эквивалентен 0,24 кал. Величина называется механическим эквивалентом теплоты.

Если величины, входящие в (1.7), выражены в разных единицах, то некоторые из этих величин нужно умножить на соответствующий эквивалент. Так, например, выражая Q в калориях, а U и A в джоулях, соотношение (1.7) нужно записать в виде

.

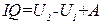В дальнейшем мы будем всегда предполагать, что Q, A и U выражены в одинаковых единицах, и писать уравнение первого начала термодинамики в виде (1.7)

При вычислении совершенной системой работы или полученной системой теплоты обычно приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует весьма малому (в пределе – бесконечно малому) изменению параметров системы. Уравнение (1.7) для элементарного процесса имеет вид:

, (1.8)

где – элементарное количество теплоты, – элементарная работа и 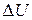– приращение внутренней энергии системы в ходе данного элементарного процесса.

Весьма важно иметь в виду, что и нельзя рассматривать как приращение величин Q и A. Соответствующее элементарному процессу изменение какой-либо величины f можно рассматривать как приращение этой величины только в том случае, если 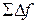, соответствующая переходу из одного состояния в другое, не зависит от пути, по которому совершается переход, т. е. если величина f является функцией состояния. В отношении функции состояния можно говорить об ее «запасе» в каждом из состояний. Например, можно говорить о запасе внутренней энергии, которым обладает система в различных состояниях.

Как мы увидим в дальнейшем, величина совершенной системой работы и количество полученной системой теплоты зависят от пути перехода системы из одного состояния в другое. Следовательно, ни Q, ни A не являются функциями состояния, в силу чего нельзя говорить о запасе тепла или работы, которым обладает система в различных состояниях.

Таким образом, в символ Δ, стоящий при A и Q, вкладывается иной смысл, чем в символ Δ, стоящий при U. Чтобы подчеркнуть это обстоятельство, в первом случае Δ снабжено штрихом. Символ Δ U означает приращение внутренней энергии, символы Δ′ Q и Δ′ A означают не приращение, а элементарное количество теплоты и работы.

Чтобы произвести вычисления, в (1.8) переходят к дифференциалам. Тогда уравнение первого начала принимает следующий вид[6]:

. (1.9)

Интегрирование (1.9) по всему процессу приводит к выражению

,

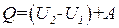тождественному уравнению (1.7).

Еще раз подчеркнем, что, например, результат интегрирования d ′ A нельзя записать в виде

.

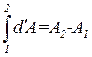Такая запись означала бы, что совершенная системой работа равна разности значений (т. е. запасов) работы во втором и первом состояниях.

1.6. Работа, совершаемая телом при изменении объема

Взаимодействие данного тела с соприкасающимися с ним телами можно охарактеризовать давлением, которое оно на них оказывает. С помощью давления можно описать взаимодействие газа со стенками сосуда, а также твердого или жидкого тела со средой (например, газом), которая его окружает. Перемещение точек приложения сил взаимодействия сопровождается изменением объема тела. Следовательно, работа, совершаемая данным телом над внешними телами, может быть выражена через давление и изменение объема тела. Чтобы найти это выражение, рассмотрим следующий пример.

Пусть газ заключен в цилиндрический сосуд, зарытый плотно пригнанным легко скользящим поршнем (рис.1.2). Если по каким-либо причинам газ станет расширяться, он будет перемещать поршень и совершать над ним работу. Элементарная работа, совершаемая газом при перемещении поршня на отрезок dh, равна

,

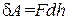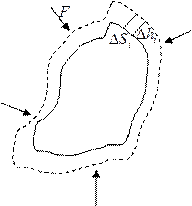
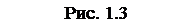где F – сила, с которой газ действует на поршень. Заменив эту силу произведением давления газа p на площадь поршня S, получим:

.

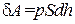Но Sdh представляет собой приращение объема газа dV. Поэтому выражение для элементарной работы можно записать следующим образом:

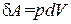. (1.10)

Величина δ A в (1.10), очевидно, является алгебраической. Действительно, при сжатии газа направления перемещения dh и силы F, с которой газ действует на поршень, противоположны, вследствие чего элементарная работа δ A будет отрицательна. Приращение объема dV в этом случае также будет отрицательным. Таким образом, формула (1.10) дает правильное выражение для работы при любых изменениях объема газа.

Если давление газа остается постоянным (для этого должна одновременно изменяться соответствующим образом температура), работа, совершаемая при изменении объема от значения V ₁ до значения V ₂, будет равна

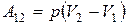. (1.11)

Если же при изменении объема давление меняется, формула (1.10) справедлива только для достаточно малых Δ V. В этом случае работа, совершаемая при конечных изменениях объема, должна вычисляться как сумма элементарных работ вида (1.10), т. е. путем интегрирования:

. (1.12)

Найденные выражения для работы справедливы при любых изменениях объема твердых, жидких или газообразных тел. Чтобы в этом убедиться, рассмотрим еще один пример. Возьмем твердое тело произвольной формы, погруженное в жидкую или газообразную среду, которая оказывает на тело одинаковое во всех точках давление p (рис. 1.3). Предположим, что тело расширяется так, что отдельные элементарные участки его поверхности Δ S_i получают различные перемещения dh_i. Тогда i -й участок совершит работу δ A_i, равную . Работа, совершаемая телом, может быть найдена как сумма работ отдельных участков:

.

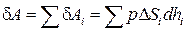Вынося за знак суммы одинаковое для всех участков p и замечая, что 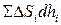дает приращение объема тела dV, можно написать: 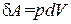, т. е. и в общем случае мы приходим к формуле (1.10).

Рис.1.4

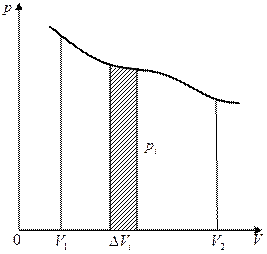
Изобразим процесс изменения объема тела на диаграмме (р, V) (рис. 1.4). Элементарной работе соответствует площадь узкой заштрихованной полоски на графике. Очевидно, что площадь, ограниченная осью V, кривой 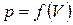и прямыми V ₁ и V ₂, численно равна работе, совершаемой при изменении объема от значения V ₁ до V ₂. Работа, совершаемая при круговом процессе, численно равна площади, охватываемой кривой (рис.1.5). Действительно, работа на участке 1–2 положительна и численно равна площади, отмеченной наклоненной вправо штриховкой (рассматривается цикл, совершаемый по часовой стрелке). Работа на участке 2–1 отрицательна и численно равна площади, отмеченной наклоненной влево штриховкой. Следовательно, работа за цикл численно равна площади, охватываемой кривой, и будет положительна при прямом цикле (т. е. таком, который совершается в направлении по часовой стрелке) и отрицательна при обратном.

Из сказанного в п.1.3 ясно, что полученные нами формулы могут быть применимы только к обратимым процессам.

Заметим, что, использовав выражение (1.10) (с переходом к дифференциалам), уравнение (1.9) первого начала термодинамики можно написать следующим образом:

. (1.13)

Дата добавления: 2015-05-09