Уравнение адиабаты идеального газа. В ходе какого-либо процесса газ, кроме уравнения состояния, подчиняется дополнительному условию, определяемому характером процесса

В ходе какого-либо процесса газ, кроме уравнения состояния, подчиняется дополнительному условию, определяемому характером процесса. Так, например, в ходе процесса, называемого изобарным, выполняется условие . При изохорном процессе выполняется условие . Наконец, при изотермическом процессе выполняется условие . Для идеального газа условие равнозначно условию

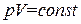. (1.38)

Уравнение (1.38) называется уравнением изотермы идеального газа, а кривая, определяемая этим уравнением, именуется изотермой.

Адиабатическим называется процесс, протекающий без теплообмена с внешней средой. Найдем уравнение, связывающие параметры идеального газа при адиабатическом процессе. Подставим в уравнение (1.13) первого начала термодинамики выражение dU для идеального газа:

.

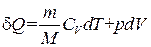Так как для адиабатического процесса , должно выполняться условие

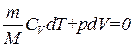. (1.39)

Теперь выразим p через V и T в соответствии с уравнением состояния идеального газа

и подставим это выражение в (1.39). В результате, сокращая на отличный от нуля множитель m / M, получим

.

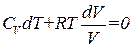Преобразуем полученное выражение следующим образом:

.

Последнее соотношение можно записать в виде

.

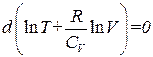Откуда следует, что при адиабатическом процессе

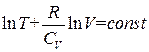. (1.40)

В соответствии с (1.35) отношение можно заменить через 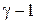, где 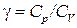. Произведя в (1.40) такую замену и пропотенцировав полученное выражение, придем к уравнению

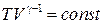. (1.41)

Полученное соотношение представляет собой уравнение адиабаты идеального газа в переменных T и V. От этого уравнения можно перейти к уравнению в переменных p и V, заменив в нем T через p и V в соответствии с уравнением состояния идеального газа,

.

Подставив это выражение в (1.41) и учтя, что m, M и R – постоянные, получим

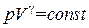. (1.42)

Соотношение (1.42) есть уравнение адиабаты идеального газа в переменных p и V. Его называют также уравнением Пуассона.

Из сопоставления уравнения адиабаты (1.42) с уравнением (1.38) следует, что адиабата идет круче, чем изотерма. Вычислим для изотермы и адиабаты в одной и той же точке (p, V) (рис.1.6). Дифференцирование уравнения (1.38) дает

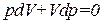
откуда для изотермы получаем

. (1.43)

Продифференцировав (1.42), получим , откуда

.

Таким образом, тангенс угла наклона адиабаты в γ раз больше, чем у изотермы. Во всех рассуждениях мы предполагали, что состояние газа в каждый момент времени характеризуется определенными значениями параметров p и T, т. е., иными словами, что рассматриваемый адиабатический процесс является обратимым. Как мы знаем, обратимым может быть только процесс, протекающий очень медленно. Вместе с тем, поскольку совершенно непроводящих тепло веществ в природе не существует, количество теплоты, которым обмениваются система с ее окружением, будет тем меньше, чем меньше продолжительность процесса. Таким образом, близкими к адиабатическому могут быть только быстро протекающие процессы. Примером такого процесса может служить сжатие и расширение, происходящие в каждой точке газа, в котором распространяется звуковая волна. Несмотря на то, что в пределах большого объема состояние газа при этом отнюдь не является равновесным (p и T в разных точках различны), поведение газа в пределах каждого достаточно малого объема вполне удовлетворительно описывается уравнением адиабаты (1.42).

Дата добавления: 2015-05-09