Внутренняя энергия и теплоемкость идеального газа

Опыт показывает, что внутренняя энергия идеального газа зависит только от температуры

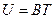. (1.23)

Здесь B – коэффициент пропорциональности, который остается постоянным в весьма широком интервале температур.

Отсутствие зависимости внутренней энергии от занимаемого газом объема указывает на то, что молекулы идеального газа подавляющую часть времени не взаимодействуют друг с другом. Действительно, если бы молекулы взаимодействовали между собой, во внутреннюю энергию входила бы потенциальная энергия взаимодействия, которая зависела бы от среднего расстояния между молекулами, т. е. от .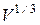

Отметим, что взаимодействие должно иметь место при столкновениях,
т. е. при сближении молекул на очень малое расстояние. Однако такие столкновения в разреженном газе происходят редко. Подавляющую часть времени каждая молекула проводит в свободном полете.

Теплоемкостью какого-либо тела называется величина, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин. Если сообщение телу количества теплоты δ Q повышает его температуру на dT, то теплоемкость по определению равна

. (1.24)

Эта величина измеряется в джоулях на кельвин (Дж/К).

Теплоемкость моля вещества, называемую молярной теплоемкостью, мы будем обозначать прописной буквой C. Измеряется она в джоулях на моль-кельвин ((Дж/(моль·К)).

Теплоемкость единицы массы вещества называется удельной теплоемкостью. Ее мы будем обозначать строчной буквой c. Измеряется c в джоулях на килограмм-кельвин (Дж/(кг·К)).

Между молярной и удельной теплоемкостями одного и того же вещества имеется соотношение

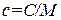. (1.25)
(M – молярная масса).

Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме (обозначается C_V), во втором – теплоемкостью при постоянном давлении (C_p).

Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами, и, следовательно, согласно первому началу термодинамики (см. (1.9)), вся теплота идет на приращение внутренней энергии тела:

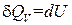. (1.26)

Из (1.26) вытекает, что теплоемкость любого тела при постоянном объеме равна

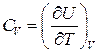. (1.27)

Такая запись подчеркивает то обстоятельство, что при дифференцировании выражения для U по T объем следует считать постоянным. В случае идеального газа U зависит только от T, так что выражение (1.27) можно представить в виде

.

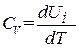(чтобы получить молярную теплоемкость, нужно взять внутреннюю энергию моля газа).

Выражение (1.23) для одного моля газа имеет вид: 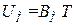. Продифференцировав его по T, получим, что 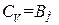. Таким образом, выражение для внутренней энергии одного моля идеального газа можно представить в виде

, (1.28)

где C_V – молярная теплоемкость газа при постоянном объеме.

Внутренняя энергия произвольной массы газа m будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся
в массе m:

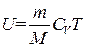. (1.29)

Если нагревание газа происходит при постоянном давлении, то газ будет расширяться, совершая над внешними телами положительную работу. Следовательно, для повышения температуры газа на один кельвин в этом случае понадобится больше количества теплоты, чем при нагревании при постоянном объеме, – часть тепла будет затрачиваться на совершение газом работы. Поэтому теплоемкость при постоянном давлении должна быть больше, чем теплоемкость при постоянном объеме.

Напишем уравнение (1.13) первого начала термодинамики для моля газа:

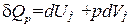. (1.30)

В этом выражении индекс p при δ Q указывает на то, что тепло сообщается газу в условиях, когда p постоянно. Разделив (1.30) на dT, получив выражение для молярной теплоемкости газа при постоянном давлении:

. (1.31)

Слагаемое 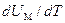равно, как мы видели, молярной теплоемкости при постоянном объеме. Поэтому формула (1.31) может быть написана следующим образом:

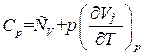. (1.32)

Величина 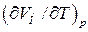представляет собой приращение объема моля газа при повышении температуры на один кельвин, получающееся в случае, когда p постоянно. В соответствии с уравнением состояния (1.17) . Дифференцируя это выражение по T, полагая , находим

.

Наконец, подставив этот результат в (1.32), получаем

. (1.33)

Уравнение (1.33) называется уравнением Майера. Таким образом, работа, которую совершает один моль идеального газа при повышении его температуры на один кельвин при постоянном давлении, оказывается равной газовой постоянной R. Отметим, что соотношение (1.33) получено с использованием уравнения состояния идеального газа и, следовательно, справедливо только для идеального газа.

Величина

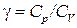(1.34)

представляет собой характерную для каждого газа величину. Для одноатомных газов это отношение близко к 5/3, для двухатомных – к 7/5, для трехатомных – к 4/3 и т. д.

Значение γ определяется числом и характером степеней свободы молекулы (то есть числом независимых переменных, с помощью которых можно описать ее движение), поскольку в молекуле помимо поступательного движения ее как целого возможны также колебания и вращение. Для величины γ можно записать

,

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы (поскольку колебательные степени свободы имеют как кинетическую, так и потенциальную энергию).

В соответствии с (1.33)

,

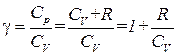откуда

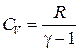. (1.35)

Подставив это значение C_V в формулу (1.29), получим следующее выражение

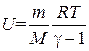. (1.36)

Сопоставление с (1.18) дает еще одно выражение для внутренней энергии идеального газа:

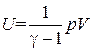. (1.37)

Дата добавления: 2015-05-09