Основные соотношения в линейном потенциометрическом датчике

Свойства потенциометрического датчика определяются его характеристикой I _H = f (x), где I _H — ток в нагрузке (например, в измерительном приборе); х — перемещение движка потенциометра (см. рис. 4.1, а) или угловое перемещение а (см. рис. 4.5).

Рассмотрим основные соотношения и характеристику линейного потенциометрического датчика, у которого намотка проволоки на каркас равномерная и сечение проволоки по всей длине одинаковое. Величина тока в нагрузке I _H (см. рис. 4.1, а) может быть найдена в соответствии с теоремой об эквивалентном генераторе, т.е.

I _H = U_аб0/ (R_i + R _H) (4.1)

где U_аб0 — напряжение на выходе потенциометрического датчика в режиме холостого хода (между точками а и б); R_i — внутреннее сопротивление датчика при заданном положении движка; R _Н— сопротивление нагрузки.

Напряжение U_aб0 определяется из выражения

U_a60 = Ur ₂(r ₁ +r ₂), (4.2)

где r ₁и r ₂— сопротивления плеч датчика, т.е. R = r ₁ + r ₂.

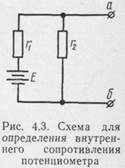
Внутреннее сопротивление датчика можно определить из рис 4.3 (пренебрегая малым внутренним сопротивлением источника тока):

R_i = r ₁ r₂ (r ₁ + r ₂). (4.3)

Подставляя (4.2) и (4.3) в (4.1), получим значение тока в нагрузке

I _H = Ur ₂ /(r ₁ + r ₂) (R_i + R _H) = Ukx/(r ₁+ r ₂) (R_i + R _H), (4.4)

где k — коэффициент пропорциональности, определяющий величину сопротивления r ₂в зависимости от перемещения движка х, т.е. r ₂ = = kх.

Анализ (4.4) показывает, что если бы внутреннее сопротивление датчика R_i - не зависело от перемещения движка х, то выходная характеристика датчика I _H= f (x) представляла бы собой прямую. Однако внутреннее сопротивление датчика зависит от перемещения х. т.е. R_i = f(R_x) (см. рис. 4.1, б), и, следовательно, ток в нагрузке в общем случае [см. (4.4)] не будет пропорционален перемещению движка (наличие в знаменателе величины R_i показывает, что зависимость I _H = f (x)—нелинейная).

Введем понятие о коэффициенте нагрузки. Коэффициентом нагрузки называется отношение сопротивления нагрузки R _H к сопротивлению датчика R, т.е.

b= R _H/ R. (4.5)

Из этой формулы следует, что если сопротивление нагрузки значительно больше сопротивления датчика, т.е. R _H >>R, то коэффициент нагрузки стремится к бесконечности, т.е.  = R _н/ R ~^oo (см. штриховую линию на рис. 4.1, б), следовательно, током в нагрузке можно пренебречь и зависимость I _H = f (x) будет также линейной. Уравнение (4.4) принимает вид

I _H = Ukx/ (RR _H). (4.6)

Если же условие R _H >>R не соблюдается, то необходимо либо учитывать погрешность, вызванную нелинейностью характеристики, либо рабочий участок характеристики ограничить участком О— х ₁с очень малой нелинейностью (см. рис. 4.1, б). Как видно из рис. 4.1, б (характеристики 1 и 2), погрешность от несогласованности сопротивлений датчика и нагрузки растет при уменьшении коэффициента нагрузки, причем при малых перемещениях движка она незначительна.

Относительная погрешность от нелинейности характеристики оценивается по формуле

(4.7)

где I _н0 — ток в нагрузке при условии, что R _н>> R.

Расчет погрешности потенциометрического датчика ведется по формуле [5]

(4.8)

где L — длина потенциометра; х — перемещение движка.

Наибольшего значения погрешность достигает при нахождении движка в среднем положении, т.е. при x = L/2 (см. рис. 4.1, в). Если в процессе работы движок может перемещаться по всей длине потенциометра, то расчет его следует вести на максимальную погрешность, которая определяется выражением [подставляем в (4.8) значение x = L/2]

(D I _H/ I _н0)_mах = R/ (R + 4 R _н).

Обозначив максимальную погрешность через s_mах, получим

s_max=1/(1+4b). (4.9)

где b = R _н/ R.

Если на выходе потенциометрического датчика подключен электронный усилитель или ламповый вольтметр с большим входным сопротивлением, то Rn^>R и погрешностью можно пренебречь.

Важным показателем качества потенциометра является плавность изменения выходного напряжения, определяющая, какое наименьшее изменение угла поворота или перемещения движка способен он различать. Тщательные измерения показывают, что выходное напряжение проволочных датчиков изменяется неплавно и не непрерывно (за исключением потенциометра с равномерной намоткой), а ступенчато. Ступенчатость обусловлена тем, что токосъемный элемент движка (см. рис. 4.2, а) не соприкасается с поверхностью провода по всей длине, а контактирует только с определенной частью отдельных витков обмотки (как бы «перескакивает»).

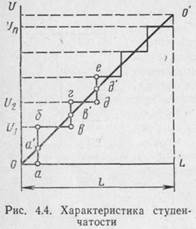
Характер ступенчатости потенциометра зависит от величины приложенного напряжения U (рис. 4.4) и полного числа витков на всей длине L рабочей части потенциометра. На рис. 4.4 приведена расчетная характеристика потенциометрического датчика в виде прямой 00'. Реальное изменение выходного напряжения показано ломаной линией 0абвгде... 0'. Анализ этих характеристик показывает, что до полного включения первого витка обмотки выходное напряжение, вместо того чтобы следовать по расчетной прямой, фактически равно нулю и определяется по оси L отрезком 0а. После включения этого витка выходное напряжение изменяется скачком и достигает значения a6 (U ₁). Соответствующее скачкообразное приращение напряжения происходит каждый раз, когда движок будет переходить с первого витка на другой и т. д. Если предположить, что потенциометр выполнен с большой точностью, то можно полагать, что расчетная прямая 00' делит вертикальные отрезки аб, вг, де и т. д. на равные части, т.е. аа' = а'б, вв = в'г и т. д.

Обозначим через п общее число витков потенциометра; тогда ошибка выходного напряжения из-за ступенчатости его характеристики

D U _ст<=± U /(2 n), (4.10)

где U — напряжение питания потенциометра.

Из формулы (4.10) следует, что для уменьшения ошибки из-за ступенчатости необходимо при данном рабочем напряжении увеличивать число витков п.

Для оценки численного значения погрешности, обусловленной ступенчатостью, вводят понятие об электрической разрешающей способности потенциометра s_P(%) — это величина прироста сопротивления или напряжения при перемещении движка потенциометра на один виток. Разрешающая способность определяет максимально возможную точность работы потенциометрического датчика.

Как уже было отмечено, для улучшения разрешающей способности потенциометра нужно увеличить число витков п. Этого можно достигнуть двумя способами: либо путем удлинения обмотки, либо уменьшением сечения провода. Однако уменьшение диаметра провода приводит к технологическим трудностям изготовления потенциометра, к ухудшению механической прочности провода и, следовательно, к сокращению срока службы и ухудшению надежности потенциометра. Удлинение же обмотки приводит к увеличению размеров потенциометра. Для устранения этого недостатка были разработаны многооборотные потенциометры.

Разрешающая способность однооборотных потенциометров принимается при расчетах не более 0,4—0,02%. Разрешающую способность или ступенчатость можно уменьшить путем применения движков с несколькими токосъемными контактами. На рис. 4.2, б изображен движок с двойным контактом, где 1, 2 — контакты движка; 3 — обмотка. Токосъемные контакты размещены таким образом, что они касаются витка в двух диаметрально противоположных точках. Это повышает надежность потенциометра, так как при параллельном включении контактов вероятность случайного нарушения электрического контакта движка с обмоткой значительно уменьшается. Постоянной разрешающей способностью обладают только линейные потенциометры.

Основными достоинствами потенциометрических датчиков являются: простота конструкции, возможность получения прямолинейной характеристики, отсутствие необходимости последующего усиления (если они применяются для целей измерения).

К недостаткам следует отнести: заниженную надежность из-за наличия скользящего электрического контакта; подгорание контактов, относительно большое перемещение движка и большое усилие для его перемещения.

Дата добавления: 2015-05-09