Проволочные тензодатчики (тензометры)

Основные понятия

ТЕНЗОМЕТРИЧЕСКИЕ ДАТЧИКИ - ТЕНЗОРЕЗИСТОРЫ

(ТЕНЗОДАТЧИКИ)

Тензодатчики, называемые также тензорезисторами, подобны тензолитовым датчикам (см. гл. V) и применяются для измерения упругих деформаций (напряжений), давлений, ускорений, малых перемещений, вибраций в различных частях механических конструкций. В основе работы тензодатчиков лежит явление тензоэффекта (тензорезистивный эффект), заключающееся в изменении активного сопротивления проводников при их механической деформации. В автоконтроле тензодатчики дают возможность определить как статические, так и динамические нагрузки.

На практике наиболее широко распространены проволочные тензодатчики, а также фольговые, пленочные и полупроводниковые.

Принцип работы проволочного тензодатчика основан на изменении активного сопротивления проволоки под действием механических усилий. Под действием деформации детали изменяются геометрические размеры проволоки и удельное сопротивление, а также сопротивление проволоки

R= r l/S. (6.1)

Представим себе (рис. 6.1), что провод длиной l, радиусом r, сечением S =pr² и объемом V = p r ² l подвергается механическому напряжению усилием Р; при этом проволока получает удлинение dl и уменьшение радиуса dr. Следовательно, новый объем проволоки V ₁= p(r — dr) ² (l + dl). Пренебрегая бесконечно малыми высших порядков, получим

V ₁ = p r ² l + p r ² dl — 2p rldr = V + dV, (6.2)

где приращение объема

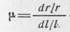
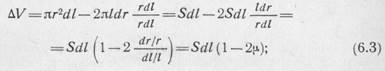-коэффициент Пуассона для материала проволоки, характеризующий уменьшение поперечных размеров проволоки при растяжении. Например, для идеальных материалов, не изменяющих при деформациях своего объема, D V = 0 и m = 0,5. Металлическая проволока имеет m = 0,24...0,4.

Для нахождения изменения сопротивления проволоки при растяжении необходимо:

· продифференцировать равенство (6.1) — закон Ома

· преобразовать выражение ldS, для чего продифференцируем объем проволоки V = lS, где S =p r ²,

dV = ldS + Sdl. (6.5)

Сравнивая (6.5) и (6.3), получим

ldS= — Sdl2 m. (6.6)

Дата добавления: 2015-05-09