Отрицание

Алгебра логики высказывание таблица истинности

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями^[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в отличие от, например, троичной логики), что высказывания могут быть только истинными или ложными.

Высказывание — термин математической логики, обозначающий формализованную структурированную запись мысли с помощью буквенных символов и логических связок, рассматриваемую с точки зрения истинностных значений. Это утверждение, для которого оценивается логическое значение: ложь или истина^[1]. Логическое высказывание принято обозначать заглавными латинскими буквами. Является основным объектом логики высказываний.

(Виды высказываний

Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.

Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.

Логическая связка — это любая логическая операция над высказыванием. Например, употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» являются логическими связками.

Элементарные логические высказывания — это высказывания не относящиеся к составным.

Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».

Связь с математической логикой

Обычная логика двухзначна, то есть приписывает высказываниям только два возможных значения: истинно оно или ложно.

Пусть 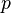— высказывание. Если оно истинно, то пишут 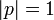, если ложно, то .

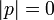Тождественно истинное высказывание обозначают символом 1, тождественно ложное — символом 0.

Существуют также многозначные логики (Яна Лукасевича, С. Клини и др.).

Основные операции над логическими высказываниями

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности (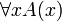) — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования (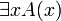) — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.)

Таблица истинности — это таблица, описывающая логическую функцию.

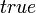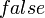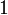Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).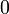

Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики

Таблицы истинности для некоторых троичных логических функций

x
y
Минимум

x
y
Максимум Минус.

x
y
Webb(x,y)

16.Логическое сложение,или дизъюнкция (+ или V)

Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):

Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Обозначается: ол

В естественном языке: соответствует союзу "или"

Принимаемые значения: лрл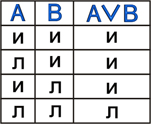

Диаграмма Эйлера-Венна: В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Примеры:

1. 10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 или 5 больше 3 (A 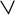B - и).
2. 10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 или 5 больше 3 (A 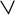B - и).
3. 10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 или 5 не больше 3 (A 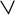B - и).
4. 10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 не делится на 2 или 5 не больше 3 (A 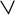B - л).

В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции).
Правило: результат равен 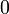, если все операнды равны 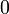; во всех остальных случаях результат равен .

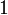Таблица истинности

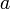
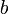
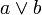
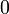
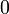
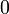
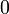
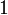
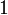
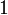
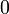
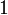
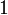
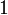
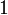
17.логическое умножение или конъюкция (точка няка и &)

Операция конъюнкция (лат. conjunctio — соединение) (логическое умножение):

Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначается: ол

В естественном языке: соответствует союзу "и"

Принимаемые значения: лрл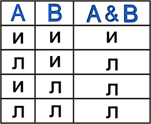

Диаграмма Эйлера-Венна: В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.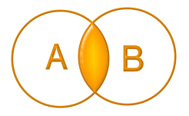

Примеры:

1. 10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 и 5 больше 3 (A B - и).
2. 10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 и 5 больше 3 (A 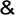B - л).
3. 10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 и 5 не больше 3 (A 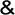B - л).
4. 10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 делится на 2 и 5 больше 3 (A 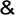B - л).

В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества 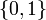. Результат также принадлежит множеству 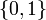. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 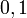может использоваться любая другая пара подходящих символов, например 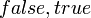или 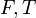или "ложь", "истина", но при таком обозначении необходимо дополнительно доопределять старшинство, например, 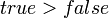, при цифровом обозначении старшинство естественно .
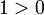Правило: результат равен 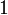, если все операнды равны 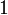; во всех остальных случаях результат равен .

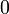Таблицы истинности:
для бинарной конъюнкции

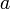
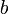
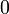
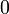
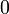
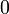
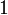
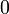
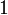
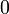
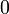
Операция инверсия (отрицание):

Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Обозначается: ол

В естественном языке: соответствует словам "неверно, что..." и частице "не"

Диаграмма Эйлера-Венна:

Принимаемые значения: лрл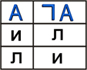

Диаграмма Эйлера-Венна: В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.

Пример: Луна — спутник Земли (А). Луна — не спутник Земли ( A)

Отрица́ние в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком перед или чертой над суждением. Синоним: логическое "НЕ".

Как в классической, так и в интуиционистской логике «двойное отрицание» A является следствием суждения A, то есть имеет место тавтология: .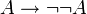

Обратное утверждение 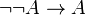верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть, отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.

Дата добавления: 2015-05-09