Правила дифференцирования

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

5) если y = f(u),

u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то , или ;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем ≠ 0, то .

Таблица производных

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u^m)' = m u^m-1 u' (m принадлежит R¹ )

2. (a^u)' = a^u lna× u'.

3. (e^u)' = e^u u'.

4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u.

6. (sin u)' = cos u× u'.

7. (cos u)' = - sin u× u'.

8. (tg u)' = 1/ cos²u× u'.

9.(ctg u)' = - u' / sin²u.

10. (arcsin u)' = u' / .

11. (arccos u)' = - u' / .

12. (arctg u)' = u'/(1 + u²).

13. (arcctg u)' = - u'/(1 + u²).

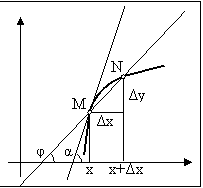
Вычислим производную степенно-показательного выражения y = u^v, (u>0), где u и v суть функции от х, имеющие в данной точке производные u', v'. Прологарифмировав равенство y=u ^v, получим ln y = v ln u. Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь: y'/y = vu'/u +v' ln u, откуда y' = y (vu'/u +v' ln u). Итак, (u ^v)'=u ^v (vu'/u+v' ln u), u > 0. Например, если y = x ^{sin x}, то y' = x ^{sin x} (sin x/x + cos x× ln x). Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой точке конечную производную y', то = y'+ α, где α→0 при Δх →0; отсюда Δy = y' Δх + αx. Главная часть приращения функции, линейная относительно Δх, называется дифференциалом функции и обозначается dy: dy = y' Δх. Если положить в этой формуле y = x, то получим dx = x'Δх = 1×Δх =Δх, поэтому dy=y'dx, т. е. символ для обозначения производной можно рассматривать как дробь. Приращение функции Δy есть приращение ординаты кривой, а дифференциал d y есть приращение ординаты касательной.

Дата добавления: 2015-05-10