
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие указания. Дифференциальные уравнения движения материальной точки
|
|
|
|
Дифференциальные уравнения движения материальной точки
Закон независимости действия сил
Закон равенства действия и противодействия
Закон пропорциональности ускорения силе
Закон инерции
Основные законы динамики
Изолированная от внешних воздействий материальная точка сохраняет состояние покоя или прямолинейного, равномерного движения до тех пор, пока действие приложенных сил не изменит это состояние.
Ускорение, приобретаемое материальной точкой, пропорционально
действующей на точку силе и направлено в сторону действия силы.
Материальные тела действуют друг на друга с силами, равными по величине и противоположными по направлению.
Ускорение, приобретаемое материальной точкой под действием нескольких сил, равно ускорению, которая получила бы точка от действия равнодействующей этой системы сил.
Из второго закона Ньютона динамики материальной точки
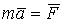 (1.1)
(1.1)
получаются две наиболее распространенные формы дифференциальных уравнений движения:
– дифференциальные уравнения движения точки в координатной форме
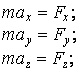 или
или 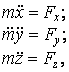 (1.2)
(1.2)
где 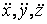 – проекции ускорения
– проекции ускорения 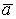 на оси декартовых координат,
на оси декартовых координат, 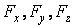 – проекции силы
– проекции силы 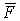 на те же оси декартовых координат;
на те же оси декартовых координат;
– дифференциальные уравнения движения точки в естественной форме
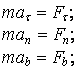 или
или  (1.3)
(1.3)
где 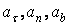 – проекции ускорения
– проекции ускорения 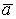 на естественные оси координат;
на естественные оси координат;
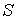 – дуговая координата точки;
– дуговая координата точки; 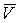 – скорость точки;
– скорость точки; 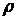 – радиус кривизны траектории;
– радиус кривизны траектории; 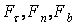 – проекции силы
– проекции силы 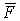 на естественные оси координат.
на естественные оси координат.
С помощью дифференциальных уравнений (1.2) и (1.3) можно решить любую задачу динамики свободной материальной точки.
3) Две основные задачи динамики.
В динамике решаются две основных задачи:
1) по заданному движению точки или системы определить силы, производящие это движение.
2) по заданным силам, действующим на точку или систему, определить движение этих объектов.
Первая основная задача динамики
Пусть движение точки массой m задано координатным способом, т.е. заданы
x = f1(t); y = f2(t); z = f3(t)
Дифференцируя дважды по t и подставляя значения  в уравнения (1):
в уравнения (1): 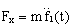 ,
, 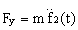 ,
, 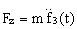 .
.
Модуль и направляющие косинусы равнодействующей найдем по формулам:
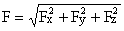 ;
; 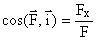 ;
; 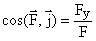 ;
; 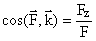
Если движение задано естественным способом: S = f(t)
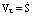 ,
, 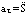 ,
,  ,
, 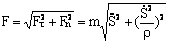 ,
, 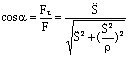
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 318; Нарушение авторских прав?; Мы поможем в написании вашей работы!