Движение м.т. под действием силы, зависящей только от координат. Одномерный случай

Движение м.т. под действием силы, зависящей только от скорости

Движение м.т. под действием силы f = f (v), зависящей только от скорости, происходит по закону:

w = f (v)/ m

В общем случае направление вектора w может не совпадать с направлением вектора скорости v. Но в данном случае мы рассматриваем одномерное движение. В противном случае сила будет зависеть от направления движения.

Для получения уравнения движения необходимо решить в общем случае нелинейное дифференциальное уравнение первого порядка относительно v:

dv / dt = f (v)/ m

∫ m / f (v) dv = ∫ dt

При ГПТК скорость преобразуется как вектор–скорость, но сила не должна измениться:

f '(v ') = f (v ' + v ₀) = f (v)

В 3-мерном пространстве уравнение движения состоит из системы трех независимых уравнений, каждая из которых решается независимо от других.

Простейшей зависимостью такой силы от скорости является линейная:

dv / dt = – k (v – v ₀)

где k – коэффициент сопротивления движению,

v ₀ – некоторая постоянная скорость, зависящая от с.о., или собственная скорость среды движению м.т. Параметр v ₀ может быть полем скорости сопротивляющейся среды.

Решим ее для постоянного v ₀:

dv /(v – v ₀) = – k dt

Проинтегрируем ее между точками t и t ₀ при v > v ₀:

ln(v (t) – v ₀) = – k (t – t ₀)

v (t) – v ₀ = –exp(– k (t – t ₀))

v (t) = v ₀ – exp(– k (t – t ₀))

При k < 0 движение происходит с приближением значения скорости м.т. к скорости v ₀, но эта скорость никогда не достигнет значения, равного v ₀, в силу свойств экспоненциальной функции: v ₀– это скорость выделенной с.о., в которой скорость м.т. со временем стремится к нулевому значению, т.е. останавливается.

Разрешим уравнение относительно координаты r:

r (t) = r ₀ + ∫ v dt

r (t) = r ₀ + ∫(v ₀ – exp(– k (t – t ₀))) dt =

= r ₀ + v ₀ (t – t ₀) + (exp(– k (t – t ₀)) – 1)/ k

При k < 0, v ₀ = 0 и t → ∞ движение происходит с замедлением и бесконечным стремлением к некоторой границе, в силу свойств экспоненциальной функции:

r_max = l im _{t →∞}[ r ₀ + (exp(– k (t – t ₀)) – 1)/ k ] =

= r ₀ +1/ k

Еще одна простейшая зависимость такой силы от скорости – тоже линейная, но всегда направленная перпендикулярно вектору скорости и некоторому направлению H:

f = e [ v ´ H ]

Под действием такой силы м.т. будет двигаться по окружности некоторого радиуса R, определяемой из уравнения:

e [ v ´ H ] = mv ²/ R

R = m / e · v ²/[ v ´ H ]

При наличии начальной тангенциальной скорости м.т. к направлению H м.т. будет двигаться одновременно по винтовой линии со скоростью в направлении H, равной начальной тангенциальной скорости м.т.

Такое движение осуществляется уже под действием силовых полей. Движение м.т. под действием силы f = f (r), зависящей только от координаты, происходит по закону:

(7.4.1)

d ² r / dt ² = f (r)

dv / dt = f (r)

Решить это уравнение проще, если воспользоваться законом сохранения энергии. Для этого заметим, что инеграл силы по координате x в одномерном случае всегда будет равен потенциальной энергии:

(7.4.2)

∫ f (r) = U (x)

Запишем уравнение закона сохранения энергии к нашему одномерному случаю:

(7.4.3)

½ v ² + U (x) = E

Это есть дифференциальное уравнение первого порядка, интегрирующееся путем разделения переменных. Имеем:

(7.4.4)

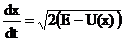
откуда:

(7.4.5)

Роль двух произвольных постоянных в решении уравнения движения играют здесь полная энергия E и постоянная интегрирования C. Поскольку кинетическая энергия является величиной существенно положительной, то при движении полная энергия всегда больше потенциальной, и движение может происходить только в тех областях пространства, где U (x)≤ E.

Пусть, например, зависимость U (x) имеет вид, изображен­ный на рис. 9. Проведя на этом же графике горизонтальную прямую, соответствующую заданному значению полной энер­гии, мы сразу же выясним возможные области движения. Так в изображенном на рис. 9 случае движение может происходить лишь в области АВ или в области справа от С,

Рис. 9. Движение м.т. в потенциальном поле.

Точки, в которых потенциальная энергия равна полной

(7.4.6)

U (x) = E

определяют границы движения. Они являются точками оста­новки, поскольку в них скорость обращается в нуль. Если об­ласть движения ограничена двумя такими точками, то движе­ние происходит в ограниченной области пространства; оно яв­ляется, как говорят, финитным. Если же область движения не ограничена или ограничена лишь с одной стороны, — движение инфинитно, частица уходит на-бесконечность.

Одномерное финитное движение является колебательным - частица совершает периодически повторяющееся движение ме­жду двумя границами (на рис. 9 в потенциальной яме АВ ме­жду точками x ₁ и x ₂). При этом согласно общему свойству об­ратимости время движения от x ₁ до x ₂ равно времени обратного движения от x ₂ до x ₁. Поэтому период колебаний Т, т. е. время, за которое точка пройдет от x ₁ до x ₂ и обратно, равен удвоенному времени прохождения отрезка x ₁ x ₂ или:

(7.4.7)

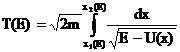
причем пределы x ₁ и x ₂ являются корнями уравнения (7.4.6), при данном значении Е. Эта формула определяет период дви­жения в зависимости от полной энергии частицы.

Движение м.т. под действием произвольных сил в 3-мерном пространстве не поддается общему решению, хотя в некоторых случаях это возможно. Такие примеры рассмотрены ниже.

Дата добавления: 2015-05-10