Теорема об изменении кинетической энергии точки

Введем понятие еще об одной основной динамической характеристике движения о кинетической энергии. Кинетической энергией материальной точки называется скалярная величина равная половине произведения массы точки на квадрат ее скорости.

Единица измерения кинетической энергии та же, что и работы (в СИ — 1 Дж). Найдем зависимость, которой связаны эти две величины.

Рассмотрим материальную точку с массой 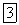, перемещающуюся из положения , где она имеет скорость 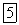в положение , где ее скорость

Для получения искомой зависимости обратимся к выражающему основной закон динамики уравнению Проектируя обе его части на касательную к траектории точки М, направленную в сторону движения, получим

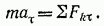
Входящее сюда касательное ускорение точки представим в виде

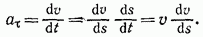
В результате найдем, что

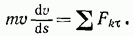
Умножим обе части этого равенства на и внесем под знак дифференциала. Тогда, замечая, что где — элементарная работа силы получим выражение теоремы об изменении кинетической энергии точки в дифференциальной форме:

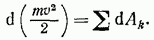
Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках найдем окончательно

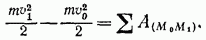
Уравнение (52) выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Случай несвободного движения. При несвободном движении точки в правую часть равенства (52) войдет работа заданных (активных) сил и работа реакции связи. Ограничимся рассмотрением движения точки по неподвижной гладкой (лишенной трения) поверхности или кривой. В этом случае реакция N (см. рис. 233) будет направлена по нормали к траектории точки и . Тогда, согласно формуле (44), работа реакции неподвижной гладкой поверхности (или кривой) при любом перемещении точки будет равна нулю, и из уравнения (52) получим

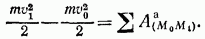
Следовательно, при перемещении по неподвижной гладкой поверхности (или кривой) изменениекинетической энергии точки равно сумме работ на этом перемещении приложенных к точке активных сил.

Дата добавления: 2015-05-10