Принцип возможных перемещений

КЛАССИФИКАЦИЯ СВЯЗЕЙ

Введенное в § 3 понятие о связях охватывает не все их виды. Поскольку рассматриваемые даже методы решения задач механики применимы вообще к системам не с любыми связями, рассмотрим вопрос о связях и об их классификации несколько подробнее.

Связями называются любого вида ограничения, которые налагаются на положения и скорости точекмеханической системы и выполняются независимо от того, какие на систему действуют заданные силы. Рассмотрим, как классифицируются эти связи.

Связи, не изменяющиеся со временем, называются стационарными, а изменяющиеся со с временем — нестационарными.

Связи, налагающие ограничения на положения (координаты) точек системы, называются геометрическими, а налагающие ограничения еще и на скорости (первые производные от координат по времени) точек системы — кинематическими или дифференциальными.

Если дифференциальную связь можно представить как геометрическую, т. е. устанавливаемую этой связью зависимость между скоростями свести к зависимости между координатами, то такая связь называется интегрируемой, а в противном случае — неинтегрируемой.

Геометрические и интегрируемые дифференциальные связи называют связями голсномньши, а неинтегрируемые дифференциальные связи — неголономньши.

По виду связей механические системы тоже разделяют на голономные (с голономными связями) и неголономные (содержащие неголономные связи).

Наконец, различают связи удерживающее (налагаемые ими ограничения сохраняются при любом положении системы) и неудерживающие, которые этим свойством не обладают (от таких связей, как говорят, система может «освобождаться»). Рассмотрим примеры.

1. Все связи, рассмотренные в § 3, являются геометрическими (голономными) и притом стационарными. Движущийся лнфт, изображенный на рис. 271, а, будет для лежащего в нем груза, когда положение груза рассматривается по отношению к осям Оху, нестационарной геометрической связью (пол кабины, реализующий связь, изменяет со временем свое положение в пространстве).

2 Положение катящегося без скольжения колеса (см. рис. 328) определяется координатой центра С колеса и углом поворота . При качении выполняется условие 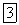или

Это дифференциальная связь, но полученное уравнение интегрируется и дает 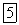, т. е. сводится к зависимости между координатами. Следовательно, наложенная связь голономная.

Заметим, что эту связь можно сразу считать геометрической, подчиняющей координаты зависимости Но тогда отсюда найдем, что одновременно и , т. е. что связь является и кинематической.

3. В отличие от колеса для шара, катящегося без скольжения по шероховатой плоскости, условие того, что скорость точки шара, касающаяся плоскости, равна нулю, не может быть сведено (когда центр шара движется не прямолинейно) к каким-нибудь зависимостям между координатами, определяющими положение шара. Это пример негалоиомной связи. Другой пример дают связи, налагаемые на управляемое движение. Например, если на движение точки (ракеты) налагается условие (связь), что ее скорость в любой момент времени должна быть направлена в другую движущуюся точку (самолет), то это условие к какой-нибудь зависимости между координатами тоже не сводится и связь является неголономной.

4. В § 3 связи, показанные на рис. являются, удерживающими, а на рис. 8 и 9 — неудерживающими (на рис. 8, а шарик может покинуть поверхность, а на рис. 9 — перемещаться в сторону точки А, сминая нить). С учетом особенностей неудерживающих связей мы сталкивались в задачах 108, 109 (§ 90) и в задаче 146 (§ 125).

Перейдем к рассмотрению еще одного принципа механики, который устанавливает общее условиеравновесия механической системы. Под равновесием (см. § 1) мы понимаем то состояние системы, при котором все ее точки под действием приложенных сил находятся в покое по отношению к инерциальной системе отсчета(рассматриваем так называемое «абсолютное» равновесие). Одновременно будем считать все наложенные на систему связи стационарными и специально это в дальнейшем каждый раз оговаривать не будем.

Введем понятие о возможной работе, как об элементарной работе, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки. Будем возможную работу активной силы обозначать символом , а возможную работу реакции N связи — символом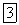

Дадим теперь общее определение понятия об идеальных связях, которым мы уже пользовались (см. § 123): идеальными называются связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю, т. е.

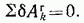
Приведенное в § 123 и выраженное равенством (52) условие идеальности связей, когда они одновременно являются стационарными, соответствует определению (98), так как при стационарных связях каждое действительное перемещение совпадает с одним из возможных. Поэтому примерами идеальных связей будут все примеры, приведенные в § 123.

Для определения необходимого условия равновесия докажем, что если механическая система с идеальными связями находится действием приложенных сил в равновесии, то при любом возможном перемещении системы должно выполняться равенство

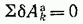
или

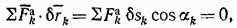
где 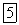— угол между силой и возможным перемещением.

Обозначим равнодействующие всех (и внешних, и внутренних) активных сил и реакций связей, действующих на какую-нибудь точку системы соответственно через . Тогда, поскольку каждая из точек системы находится в равновесии, , а следовательно, и сумма работ этих сил при любом перемещении точки будет тоже равна нулю, т. е. . Составив такие равенства для всех точек системы и сложив их почленно, получим

Но так как связи идеальные, представляют собой возможные перемещения точек системы, то вторая сумма по условию (98) будет равна нулю. Тогда равна нулю и первая сумма, т. е. выполняется равенство (99). Таким образом, доказано, что равенство (99) выражает необходимое условие равновесия системы.

Покажем, что это условие является и достаточным, т. е. что если к точкам механической системы, находящейся в покое, приложить активные силы удовлетворяющие равенству (99), то система останется в покое. Предположим обратное, т. е. что система при этом Придет в движение и некоторые ее точки совершат действительные перемещения . Тогда силы совершат на этих перемещениях работу и по теореме об изменении кинетической энергии будет:

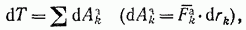
где, очевидно, , так как вначале система была в покое; следовательно, и . Но при стационарных связях действительные перемещения совпадают с какими-то из возможных перемещений и на этих перемещениях тоже должно быть что противоречит условию (99). Таким образом, когда приложенные силы удовлетворяют условию (99), система из состояния покоя выйти не может и это условие является достаточным условием равновесия.

Из доказанного вытекает следующий принцип возможных перемещений: для равновесия механической системыс идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю. Математически сформулированное условие равновесия выражается равенством (99), которое называют также уравнением возможных работ. Это равенство можно еще представить в аналитической форме (см. § 87):

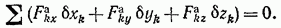
Принцип возможных перемещений устанавливает общее условие равновесия механической системы, не требующее рассмотрения равновесия отдельных частей (тел) этой системы и позволяющее при идеальных связях исключить из рассмотрения все наперед неизвестные реакции связей.

Дата добавления: 2015-05-10