Потенциальная энергия. Закон сохранения механической энергии

Для потенциального силового поля можно ввести понятие о потенциальной энергии как о величине, характеризующей «запас работы», которым обладает материальная точка в данном пункте силового поля. Чтобы сравнивать между собой эти «запасы работы», нужно условиться о выборе нулевой точки О, в которой будем условно считать «запас работы» равным нулю (выбор нулевой точки, как и всякого начала отсчета, производится произвольно). Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое

Из определения следует, что потенциальная энергия П зависит от координат х, у, z точки М, т. е. что

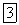Будем в дальнейшем считать нулевые точки для функций совпадающими. Тогда и по формуле значение силовой функции в точке М поля. Таким образом,

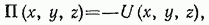
т. е. потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком.

Отсюда видно, что при рассмотрении всех свойств потенциального силового поля вместо силовой функцииможно пользоваться понятием потенциальной энергии. В частности, работу потенциальной силы вместо равенства (57) можно вычислять по формуле

Следовательно, работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном ее положениях.

Выражения потенциальной энергии для известных нам потенциальных силовых полей можно найти из равенств (59) - (59”), учитывая, что 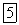. Таким образом, будет:

1) для поля силы тяжести (ось z вертикально вверх)

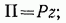
2) для поля силы упругости (линейного)

3) для поля силы тяготения

Потенциальная энергия системы определяется так же, как и для одной точки, а именно: потенциальная энергия П механической системы в данном ее положении равна работе, которую произведут силы поля при перемещении системы из данного положения в нулевое,

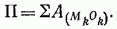
При наличии нескольких полей (например, полей сил тяжести и сил упругости) для каждого поля можно брать свое нулевое положение.

Зависимость между потенциальной энергией и силовой функцией будет такой же, как и для точки, т. е.

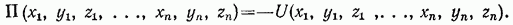
Закон сохранения механической энергии. Допустим, что все действующие на систему внешние и внутренние силы потенциальны. Тогда

Подставляя это выражение работы в уравнение (50), получим для любого положения системы: или

Следовательно, при движении под действием потенциальных сил сумма кинетической и потенциальной энергий системы в каждом ее положении остается величиной постоянной. В этом и состоит закон сохранения механической энергии, являющийся частным случаем общего физического закона сохранения энергии.

Величина называется полной механической энергией системы, а сама механическая система, для которой выполняется закон консервативной системой.

Пример. Рассмотрим маятник (рис. 320), отклоненный от вертикали на угол и отпущенный без начальной скорости. Тогда в начальном его положении , где Р — вес маятника; z — координата его центра тяжести. Следовательно, если пренебречь всеми сопротивлениями, то в любом другом положении будет или

Рис. 320

Таким образом, выше положения центр тяжести маятника подняться не может. При опускании маятника егопотенциальная энергия убывает, а кинетическая растет, при подъеме, наоборот, потенциальная энергия растет, а кинетическая убывает.

Из составленного уравнения следует, что

Таким образом, угловая скорость маятника в любой момент времени зависит только от положения, занимаемого его центром тяжести, и в данном положении всегда принимает одно и то же значение. Такого рода зависимости имеют место только при движении под действием потенциальных сил.

Диссипативные системы. Рассмотрим механическую систему, на которую кроме потенциальных сил действуют неизбежные в земных условиях силы сопротивления (сопротивление среды, внешнее и внутреннее трение). Тогда из уравнения (50) получим: или

где - работа сил сопротивления. Так как силы сопротивления направлены против движения, то величина всегда отрицательная Следовательно, при движении рассматриваемой механической системыпроисходит убывание или, как говорят, диссипация (рассеивание) механической энергии. Силы, вызывающие эту диссипацию, называют диссипативными силами, а механическую систему, в которой происходит диссипация энергии, — диссипативной системой.

Например, у рассмотренного выше маятника (рис. 320) благодаря трению в оси и сопротивлению воздухамеханическая энергия будет) со временем убывать, а его колебания будут затухать; это диссипативная система.

Полученные результаты не противоречат общему закону сохранения энергии, так как теряемая диссипативной системой механическая энергия переходит в другие формы энергии, например в теплоту.

Однако и при наличии сил сопротивления механическая система может не быть диссипативной, если теряемая энергия компенсируется притоком энергии извне. Например, отдельно взятый маятник, как мы видели, будет диссипативной системой. Но у маятника часов потеря энергии компенсируется периодическим притоком энергии извне за счет опускающихся гирь или заводной пружины, и маятник будет совершатьнезатухающие колебания, называемые автоколебаниями.

От вынужденных колебаний (см. § 96) автоколебания отличаются тем, что они происходят не под действием зависящей от времени возмущающей силы и что их амплитуда, частота и период определяются свойствами самой системы (у вынужденных колебаний амплитуда, частота и период зависят от возмущающей силы).

Дата добавления: 2015-05-10