Принцип Даламбера для материальной точки

Принцип Даламбера и метод кинетостатики

В предыдущих лекциях рассматривались способы решения задач динамики, основанные на законах Ньютона. В теоретической механике разработаны и другие способы решения динамических задач, в основе которых лежат некоторые иные исходные положения, называемые принципами механики.

Важнейшим из принципов механики является принцип Даламбера. С принципом Даламбера тесно связан метод кинетостатики — способ решения задач динамики, в котором динамические уравнения записываются в форме уравнений равновесия. Метод кинетостатики широко применяется в таких общеинженерных дисциплинах, как сопротивление материалов, теория механизмов и машин, в других областях прикладной механики. Принцип Даламбера результативно используется и внутри самой теоретической механики, где с его помощью созданы эффективные способы решения задач динамики.

Пусть материальная точка массы совершает несвободное движение относительно инерциальной системы координат Oxyz под действием активной силы и реакции связи R (рис. 57).

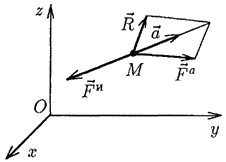
Рис. 57.

Определим вектор

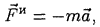
численно равный произведению массы точки на ее ускорение и направленный противоположно вектору ускорения. Вектор 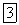имеет размерность силы и называется силой инерции (даламберовой) материальной точки.

Принцип Даламбера для материальной точки сводится к следующему утверждению: если к силам, действующим на материальную точку, условно присоединить силу инерции точки, то получим уравновешенную систему сил, т. е.

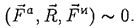
Вспоминая из статики условие равновесия сходящихся сил, принцип Даламбера можем записать также в следующей форме:

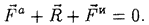
Легко видеть, что принцип Даламбера эквивалентен основному уравнению динамики, и наоборот, из основного уравнения динамики следует принцип Даламбера. Действительно, перенося в последнем равенстве вектор в другую часть равенства и заменяя 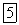на , получаем основное уравнение динамики. Наоборот, перенося в основном уравнении динамики член та в одну сторону с силами и используя обозначение , получаем запись принципа Даламбера.

Принцип Даламбера для материальной точки, будучи вполне эквивалентным основному закону динамики, выражает этот закон в совершенно иной форме — в форме уравнения статики. Это дает возможность пользоваться при составлении уравнений динамики методами статики, что и называется методом кинетостатики.

Метод кинетостатики особенно удобен при решении первой задачи динамики.

Пример. Из наивысшей точки гладкого сферического купола радиуса R соскальзывает материальная точка М массы с пренебрежимо малой начальной скоростью (рис. 58). Определить, в каком месте точка сойдет с купола.

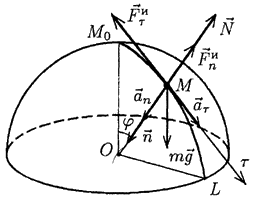
Рис. 58.

Решение. Точка будет двигаться по дуге некоторого меридиана . Пусть в некоторый (текущий) момент радиус ОМ составляет с вертикалью угол . Раскладывая ускорение точки а на касательное ) и нормальное представим силу инерции точки также в виде суммы двух составляющих:

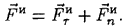
Касательная составляющая силы инерции имеет модуль и направлена противоположнокасательному ускорению, нормальная составляющая — модуль и направлена противоположнонормальному ускорению.

Добавляя эти силы к фактически действующим на точку активной силе и реакции купола N, составляем уравнение кинетостатики

Проектируя это векторное уравнение на направления касательной и главной нормали, получаем два уравнения кинетостатики в скалярной форме:

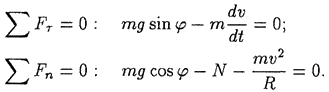
Из второго уравнения находим

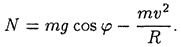
Реакция N окончательно найдется после того, как будет определена величина v и подставлена в это выражение.

Для определения v служит первое уравнение, которое является дифференциальным уравненим и требует интегрирования. Однако можно избежать интегрирования, если воспользоваться теоремой об изменениикинетической энергии. Применяя эту теорему для точки М на участке траектории и учитывая, что (работу совершает только сила тяжести), получаем:

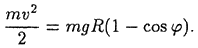
Отсюда находим

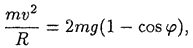
и далее

В момент отделения от купола реакция N равна нулю. Следовательно, точка сойдет с купола при

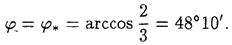
Дата добавления: 2015-05-10