
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вказівки та зразки розв’язування задач. 2 страница
|
|
|
|

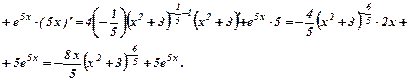
б)  . Скористаємося правилом диференціювання частки двох диференційованих функцій, а потім знаходимо похідні складних функцій:
. Скористаємося правилом диференціювання частки двох диференційованих функцій, а потім знаходимо похідні складних функцій: 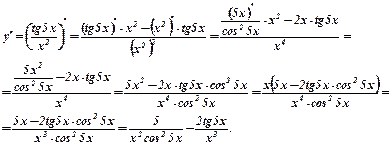
в) 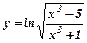 .
.
Задану функцію прологарифмуємо, а пізніше знаходимо як похідну складної функції:
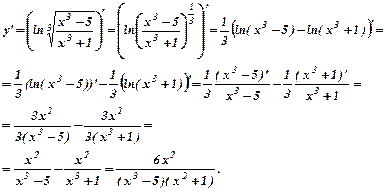
9. Підприємство за місяць виготовляє х одиниць продукції. Сумарні витрати виробництва описуються функцією  ,
, 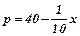 - залежність між питомою ціною і кількістю одиниць продукції х, яку можна продати по цій ціні. Розрахувати, за яких умов прибуток буде максимальним. Визначити маржинальні і сумарні витрати, прибуток при цих умовах.
- залежність між питомою ціною і кількістю одиниць продукції х, яку можна продати по цій ціні. Розрахувати, за яких умов прибуток буде максимальним. Визначити маржинальні і сумарні витрати, прибуток при цих умовах.
Розв’язування. Прибуток 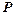 визначається як різниця між доходами і сумарними витратами виробництва
визначається як різниця між доходами і сумарними витратами виробництва 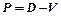 .
.
В нас дохід - 
сумарні витрати - 
прибуток  -
- 
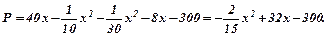
Знайдемо маржинальний прибуток -  .
.
Максимальним прибуток буде тоді, коли  оскільки
оскільки 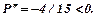
При цьому 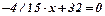 ;
; 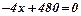 ;
; 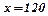 .
.
Отже, щоб прибуток був максимальним, треба випускати 120 од. продукції.
Маржинальні витрати - 
сумарні витрати
 .
.
Максимальний прибуток
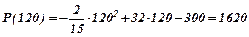 .
.
10. Знайти розміри відкритого басейну з квадратним дном об’ємом 32 м3, за яких на облицювання його стін і дна пішла б найменша кількість матеріалу.
Розв’язування. Нехай дно басейну - квадрат 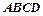 з стороною
з стороною 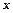 , а висота басейну
, а висота басейну 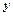 . Площа дна басейну:
. Площа дна басейну: 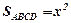 . Об’єм басейну:
. Об’єм басейну: 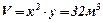 . Площа, яка необхідна для облицювання відкритого
. Площа, яка необхідна для облицювання відкритого
басейну 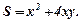 Оскільки
Оскільки  то
то 
Дослідимо функцію S(x).
Знайдемо її похідну 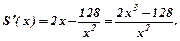
Знаходимо критичні точки: 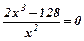 ,
, 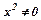 ,
,
 .
.
 Вияснимо, як поводить себе функція при переході через критичну точку
Вияснимо, як поводить себе функція при переході через критичну точку  .
.
Обчислимо:  ,
,

Оскільки, похідна функції змінює знак з “-” на “+” при переході через цю критичну точку, то точка  є точкою мінімуму.
є точкою мінімуму.
При ширині дна квадратної форми 4 м, площа облицювання відкритого басейну буде найменша.
Знайдемо висоту басейну 
Отже, розміри відкритого басейну будуть такі: дно квадратної форми має сторону квадрата 4м, висота басейну 2м.
11. При відомій функції попиту 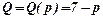 і пропозиції S=S(p)=р+1, де Q і S -кількість товару; p -ціна товару.
і пропозиції S=S(p)=р+1, де Q і S -кількість товару; p -ціна товару.
Знайти:
а) рівноважну ціну, тобто ціну, при якій попит і пропозиція врівноважуються;
б) еластичність попиту і пропозиції для рівноважної ціни;
в) зміну доходу при підвищенні ціни на 5% від рівноважної.
Розв’язування.
а) рівноважна ціна – ціна, при якій попит і пропозиція врівноважуються. Тому, рівноважна ціна визначається з рівняння 
 р=3 грн.
р=3 грн.
б) знаходимо еластичність попиту і пропозиції за формулами:


В даному випадку
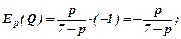

Для рівноважної ціни р=3 маємо 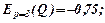
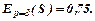
Знайдені значення еластичності за абсолютною величиною менші за 1, тоді і попит, і пропозиція даного товару при рівноважній ціні нееластичні відносно ціни, тобто зміна ціни не призведе до різкої зміни попиту і пропозиції. Так, при підвищенні ціни на 1%, попит зменшиться на
0,75%, а пропозиція підвищиться на 0,75%.
б) при підвищенні ціни p на 5% від рівноважної, попит зменшиться на 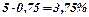 , а дохід зросте на 3,75%.
, а дохід зросте на 3,75%.
12. Дослідити та побудувати ескіз графіка функції  .
.
Розв’язування.
1. Знаходимо область визначення функції: ] -¥; 2 [È] 2; +¥ [.
2. Знаходимо точки перетину прямої з осями координат.
Якщо y=f(x) перетинає вісь Ох, то у=0. Якщо у=0, то х=0.
3. Досліджуємо функцію на парність.
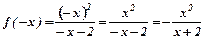 . Функція є ні парна, ні непарна.
. Функція є ні парна, ні непарна.
4. Досліджуємо функцію на неперервність.
В т. х=2 функція має розрив (знаменник рівний нулю, функція невизначена.).  . Це є розрив ІІ роду.
. Це є розрив ІІ роду.
5. Знаходимо асимптоти кривої. Вертикальна асимптота х=2, тому що  .
.
Похилу асимптоту шукаємо у вигляді y=kx+b, де 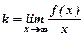 ,
,
b = 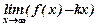 .
.
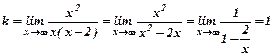 ;
;
 .
.
Отже, рівняння похилої асимптоти має вигляд: у=х+2.
6. Досліджуємо функцію на екстремум:

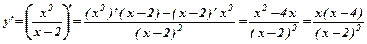
Критичні точки: х=0, х=2, х=4.
Зобразимо числову пряму і проміжки монотонності:
 |
т. х=0 – точка максимуму, f(0)=0;
т. х=4 – точка мінімуму, f(4)=  .
.
Зробимо малюнок.
13. Мале підприємство виробляє товари А і В. Загальні щоденні витрати V (у гривнях) на виробництво х одиниць товару А та у одиниць товару В відомі: V=320 – 14х-10у+ 0, 2 х2+ 0, 1 у2. 1)Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними.
Розв’язування. Загальна функція витрат відома: V=320–14x–10y+0, 2х2+0,1 у. 2 Щоб знайти кількість одиниць товарів х товару А і у товару В, необхідно дослідити цю функцію на екстремум.
Знайдемо частинні похідні І-го порядку 
Прирівнюючи їх до нуля,  одержимо систему рівнянь
одержимо систему рівнянь 




Знайдемо частинні похідні II порядку: 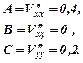
Обчислимо D=АС-В2=0, 4  0, 2-0=0, 08 > 0 і А=0, 4 > 0
0, 2-0=0, 08 > 0 і А=0, 4 > 0
Отже, функція витрат при х =35, у=50 досягає мінімуму. Це означає, що для того, щоб загальні витрати підприємства були мінімальними, необхідно виробити 35 одиниць товару А і 50 одиниць товару В.
14. Нехай виробнича функція визначається функцією Кобба-Дугласа. Щоб збільшити випуск продукції на 5%, треба збільшити фонди на 10% або чисельність робітників на 15%. В 2001 році один робітник за місяць виготовляв продукції на 2000 грн., а всього робітників було 1000. Основні фонди оцінювались в 4 млн. грн. Записати виробничу функцію, величину середньої фондовіддачі і середньої продуктивності праці, еластичність випуску по праці і по фондах.
Розв’язування. Еластичність випуску по праці 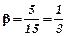 , а по фондах
, а по фондах 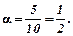 Отже, функція Кобба-Дугласа має вигляд:
Отже, функція Кобба-Дугласа має вигляд:  ,
,
 Підставляючи інші величини, одержимо:
Підставляючи інші величини, одержимо:
 , тобто
, тобто
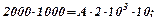

Отже, шукана виробнича функція  Середня фондовіддача дорівнює
Середня фондовіддача дорівнює 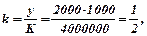 а середня продуктивність
а середня продуктивність 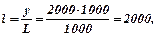
 ,
,  .
.
15. Знайти невизначені інтеграли: а) 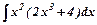 ,
,
б) 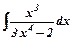 , в)
, в)  , г)
, г)  , д)
, д) 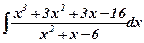 , е)
, е) 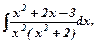 є)
є) 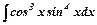 ,
,
ж) 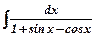 .
.
Розв’язування.
а)  .
.
Зробимо підстановку: 
Продиференціюємо: 
 . Тому
. Тому
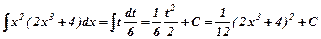
б) 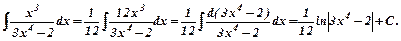
в) 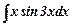 .
.
Застосовуємо метод інтегрування за частинами: 
Вибираємо: u=x, dv=sin3xdx. Тоді du=dx, v= 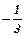 cos3x.
cos3x.
Тобто: 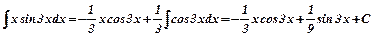 .
.
г) 
Знову інтегруємо методом інтегрування за частинами.
Підінтегральний вираз є добутком показникової функції на тригонометричну. Виберемо u= 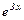 , а dv =
, а dv =  . Тоді
. Тоді  ,
,  Застосуємо двічі цю формулу. Два разиза u беремо
Застосуємо двічі цю формулу. Два разиза u беремо 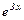 . Одержуємо
. Одержуємо  .
.
Знаходимо шуканий інтеграл:

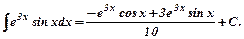
г) 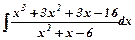 .
.
Підінтегральний раціональний дріб неправильний.
Виділяємо цілу частину:


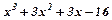
| 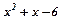
| ||||
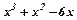
| x+2+ 
| ||||

| |||||
 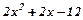
| |||||
| 7x-4 |
 .
.
Використовуючи метод невизначених коефіцієнтів, розкладаємо дріб на суму простих:  ;
; 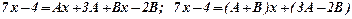 ;
;
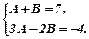
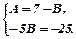 В=5; А=2. Одержимо:
В=5; А=2. Одержимо:
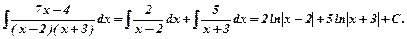 Тобто
Тобто 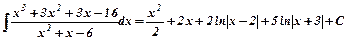 .
.
е) 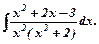
Розкладемо підінтегральну функцію, яка є правильним раціональним дробом, на суму найпростіших дробів за допомогою неозначених коефіцієнтів 
 Звідси,
Звідси, 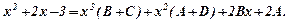
Прирівнюємо коефіцієнти при однакових степенях 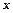 :
:
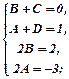

 .
.
Тоді 
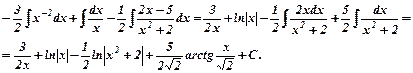
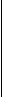 є)
є) 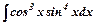 .
.
Враховуємо, що cos3x=cos2xcosx, та cosxdx=dsinx. Тоді
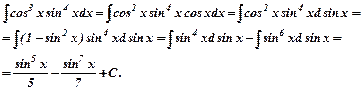
ж) 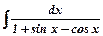 .
.
За допомогою універсальної підстановки  , даний інтеграл зводимо до інтегралу від раціонального дробу. Використавши формули
, даний інтеграл зводимо до інтегралу від раціонального дробу. Використавши формули

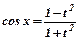 ;
; 
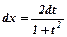 , отримаємо:
, отримаємо:
 . Одержимо інтеграл від правильного дробу. Розкладемо підінтегральну функцію на прості дроби:
. Одержимо інтеграл від правильного дробу. Розкладемо підінтегральну функцію на прості дроби: 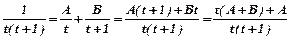 . Звідси:
. Звідси:  . Прирівнюємо коефіцієнти при однакових степенях
. Прирівнюємо коефіцієнти при однакових степенях 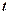 і складаємо систему рівнянь:
і складаємо систему рівнянь:
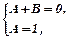


Тоді,

16. Обчислити визначений інтеграл 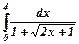 .
.
Розв’язування. Зробимо підстановку 
 .
.
Продиференціюємо цю рівність  .
.
Встановимо нові межі інтегрування.
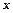
| ||
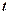
|
При  , при
, при 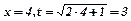 . Тоді
. Тоді

17. Обчислити площу криволінійної трапеції, обмеженої лініями 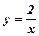 ,
, 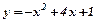 .
.
Розв’язування. Для знаходження меж інтегрування знайдемо точки перетину ліній, розв’язавши систему рівнянь.

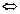
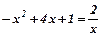
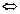
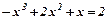
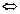
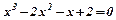
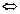
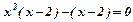
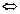
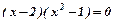
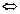
 ;
;  ;
;  .
.
 Отже, площа фігури, яку треба знайти, обмежена заданими кривими, що перетинаються у точках з абсцисами
Отже, площа фігури, яку треба знайти, обмежена заданими кривими, що перетинаються у точках з абсцисами 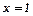 ,
,  .
.

18. Обчислити об’єм тіла обертання утвореного обертанням навколо осі Ох фігури, обмеженої лініями 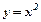 ,
,  .
.
Розв’язування. Щоб знайти межі інтегрування розв’яжемо систему рівнянь

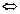

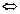
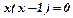
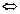
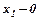 ,
, 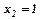 .
.
Об’єм тіла обертання знаходиться за формулою
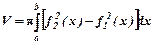 .
.
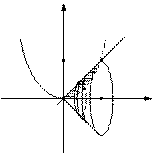 Отже, на основі цього маємо
Отже, на основі цього маємо

 (куб. од.).
(куб. од.).
19. Швидкості зміни витрат і доходу підприємства після початку його діяльності визначались формулами:

 і
і 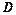 вимірювали у мільйонах гривень, а
вимірювали у мільйонах гривень, а 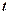 - у роках. Визначити тривалість прибуткового існування підприємства і знайти загальний прибуток, що одержали за цей час.
- у роках. Визначити тривалість прибуткового існування підприємства і знайти загальний прибуток, що одержали за цей час.
Розв’язування. Оптимальний час 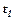 для прибутку підприємства одержимо з умови
для прибутку підприємства одержимо з умови 

Отже, підприємство було прибутковим 1 рік. За цей час одержано прибутку:

20. Знайти загальний розв’язок (загальний інтеграл) диференціальних рівнянь та розв’язати задачу Коші для тих рівнянь, де вказані початкові умови.
а)  , б)
, б)  ;
; 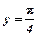 при
при 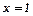 , в)
, в)  , г)
, г)  , д)
, д)  е)
е) 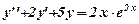 , є)
, є)  , ж)
, ж)  .
.
Розв’язування.
а)  . Це рівняння з відокремлюваними змінними. Розділимо змінні, поділивши обидві частини рівняння на
. Це рівняння з відокремлюваними змінними. Розділимо змінні, поділивши обидві частини рівняння на 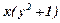 . Одержимо
. Одержимо 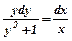 . Проінтегруємо одержане рівняння
. Проінтегруємо одержане рівняння  ;
; 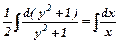 ,
,  .
.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 10751; Нарушение авторских прав?; Мы поможем в написании вашей работы!

