Вводные замечания

Лекция 7. РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Инженеру-исследователю в своей деятельности постоянно приходится сталкиваться с дифференциальными уравнениями, так как большая часть законов физики при их математическом моделировании сводится к дифференциальным уравнениям. В связи с этим решение дифуравнений является одной из важнейших математических задач.

Дифференциальным уравнением называется уравнение, в котором искомой является функция, а уравнение задает связь между значениями независимых переменных, искомой функцией и ее производными.

В зависимости от числа независимых переменных ДУ делятся на две различные группы: обыкновенные ДУ, содержащие одну независимую переменную, и уравнения в частных производных, содержащие несколько независимых переменных.

Рассмотрим обыкновенные ДУ.

Общий вид ОДУ

F (x, y, y^’, …, y⁽ⁿ⁾) = 0, (7.1)

где x – независимая переменная;

y – функция;

y ^’,…, y⁽ⁿ⁾ – производные;

n – наивысший порядок производной, порядок ДУ.

В ряде случаев из общей записи ДУ (7.1) удается выразить старшую производную в явном виде, например,

y ^” = f (x, y, y^’).

Такая форма записи называется уравнением, разрешенным относительно старшей производной.

Решением ДУ (7.1) называется всякая функция y = φ (x), которая после ее подстановки в уравнение превращает его в тождество.

Дифференциальное уравнение, как правило, имеет бесконечное множество решений, зависящее от некоторого количества (определяемого порядком ДУ) произвольных постоянных С ₁, С ₂, …, С_n.

Общее решение ОДУ (7.1) имеет вид

у = φ (x, С ₁, С ₂, …, С_n).

Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения, например, для уравнения первого порядка:

- общее решение у = φ (x, С);

- частное решение, если С = С ₀ (определенное значение) у = φ (x, С ₀).

Исследователя обычно интересует частное решение. Чтобы его получить, необходимо учитывать не только особенности изменения явления, описываемого ДУ (7.1), но и дополнительные условия, которые характеризуют это явление. Количество дополнительных условий должно быть равно количеству произвольных постоянных, то есть порядку n.

Дифференциальное уравнение вместе с дополнительными условиями называется задачей. Если х является временем (что характерно для эволюционных или динамических процессов), то необходимо учесть состояние в начальный момент времени х ₀, а если х – координата, которая может изменяться от а до b (например, прогиб балки под действием постоянной силы), то необходимо учесть состояние системы (балки) на ее границах – в точках а и b.

Таким образом, возможно существование двух типов дополнительных условий и соответственно двух типов задач:

1. Начальные условия (всего n условий) у (х ₀)= у ₀, 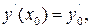…, 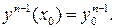Задача решения ОДУ (7.1) с начальными условиями, заданными в одной точке, называется задачей Коши.

2. Граничные (краевые) условия (всего n условий) у (а)= у_а, 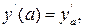…, у (b)= у_b, 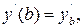…. Задача решения ОДУ (7.1) с граничными условиями называется краевой или двухточечной задачей.

7.2 Как решать ДУ

Целью решения ДУ является получение функции у = φ (x). Эта функция может быть задана графическим, аналитическим и табличным способом. Поэтому методы решения ДУ (7.1) делятся на графические, аналитические и численные.

Графические методы используются при качественном исследовании ДУ и состоят в построении интегральной кривой.

Аналитические методы дают решение уравнения в виде формулы и делятся на точные и приближенные.

Точные методы рассматриваются в вузовском курсе. Они дают точные решения, но могут быть использованы для узкого класса задач.

Приближенные аналитические методы дают функцию, являющуюся аппроксимацией точного решения. Для получения такой функции либо заменяют исходное ДУ близким к нему, но допускающим аналитическое решение, либо задаются видом решения.

Основной проблемой, возникающей при этом является проблема точности. Выход состоит в использовании идеи о разбиении области изменения независимой переменной х на малые отрезки и решении ДУ на каждом отрезке.

Этот подход иллюстрируем следующим рисунком.

1 – точное решение уравнения; 2 – аппроксимация решения линейной функцией для всей области; 3 – аппроксимация решения при разбиении области изменения х [ a, b ] на мелкие отрезки.

Видно, что замена линейной функции 2 кусочно-линейной функцией 3 значительно повышает точность решения.

Дальнейшее развитие рассматриваемой идеи привело к появлению численных методов решения ДУ, результатом которых является таблица значений функции в определенных точках (узлах).

7.3 Одношаговые методы решения задачи Коши

Задачу Коши можно сформулировать для ДУ первого порядка следующим образом.

Пусть дано ДУ y ^’ = f (x, y) c начальным условием y (x ₀) = y ₀. Требуется найти функцию y = f (x), удовлетворяющую как указанному уравнению, так и начальному условию.

Обычно численное решение этой задачи получают, вычисляя сначала значение производной в точке х ₀, а затем задавая малое приращение х и переходя к новой точке x ₁ = x ₀ + h. Положение новой точки определяется по наклону кривой, вычисленному с помощью ДУ.

Таким образом, график численного решения представляет собой последовательности коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y = f (x).

Сам численный метод определяет порядок действия при переходе от данной точки кривой к следующей.

В одношаговых методах для нахождения следующей точки на кривой y = f (x) требуется информация лишь об одном предыдущем шаге. К одношаговым относятся метод Эйлера и методы Рунге-Кутта.

7.3.1 Метод Эйлера (схема ломаных)

Является сравнительно грубым и применяется в основном для ориентировочных расчетов. Основан на разложении функции у в ряд Тейлора в окрестности точки х ₀:

y (x ₀ + h) = y (x ₀) + h y^’ (x ₀) + 1/2 h ² y” (x ₀) + …

Если шаг интегрирования h мал, то члены ряда, содержащие h во второй и более высоких степенях, малы. Поэтому ими можно пренебречь. Тогда

y (x ₀ + h) = y (x ₀) + h y^’ (x ₀).

Значение y^’ (x ₀) находим из ДУ, подставив в него начальное условие.

Этот процесс можно продолжить, используя следующее соотношение

y_{i +1} = y_i + h f (x_i, y_i), i = 0, 1, …, n – 1.

Графически метод представляется следующим образом

Погрешность этого метода пропорциональна шагу h.

Большая погрешность – главный недостаток этого метода. Точность метода Эйлера можно повысить, улучшив аппроксимацию производной. Это можно сделать, используя среднее значение производной в начале и конце интервала.

Дата добавления: 2015-05-26