Пример 7.2

Пример 7.1.

Решить ДУ на интервале [0, 1] с шагом h = 0,25 методом Эйлера. Начальные условия: y (x ₀) = у ₀ = 0.

Решение выполняется по формуле y_{i +1} = y_i + h f (x_i, y_i).

Первый шаг: i = 0, x ₀ = 0, y ₀ = 0

у _{0 +1=1} = y ₀ + h (2 x ₀ – y ²₀ + х ⁴₀) = 0 + 0,25·(2∙0 – 0² + 0⁴) = 0.

Второй шаг: i = 1, x ₁ = x ₀ + h = 0 + 0,25 = 0,25, y ₁ = 0

у _{1 +1=2} = y ₁ + h (2 x ₁ – y ²₁ + х ⁴₁) = 0 + 0,25·(2∙0,25 – 0² + 0,25⁴) = 0,126.

Третий шаг: i = 2, x ₂ = x ₁ + h = 0,25 + 0,25 = 0,5, y ₂ = 0,126

у _{2 +1=3} = y ₂ + h (2 x ₂ – y ²₂ + х ⁴₂) = 0,126 + 0,25·(2∙0,5 – 0,126² + 0,5⁴) = 0,3877.

Четвертый шаг: i = 3, x ₃ = x ₂ + h = 0,5 + 0,25 = 0,75, y ₃ = 0,3877

у _{3 +1=4} = y ₃ + h (2 x ₃ – y ²₃ + х ⁴₃) = 0,3877 + 0,25·(2∙0,75 – 0,3877² + 0,75⁴) = 0,8042.

Метод Эйлера может быть применен к решению систем дифференциальных уравнений и ДУ высших порядков. Однако в последнем случае ДУ должны быть приведены к системе ДУ первого порядка.

Пусть задана система двух уравнений первого порядка

с начальными условиями у (х ₀) = у ₀, z (х ₀) = z ₀.

Приближенные значения у (х_i) ≈ у_i и z (х_i) ≈ z_i находятся по формулам

y_{i +1} = y_i + Δ y_i, z_{i +1} = z_i + Δ z_i,

где

Δ y_i = hf ₁(x_i, y_i, z_i), Δ z_i = hf ₂(x_i, y_i, z_i) i = 0, 1, 2, …

Применяя метод Эйлера, решить систему ДУ 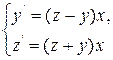при начальных условиях у (0) = 1,0000 z (0) = 1,0000 на отрезке [0, 0,6] с шагом h = 0,1. Вычисления вести с одним запасным знаком.

Покажем часть вычислений:

- первый шаг: i = 0, х ₀ = 0, y ₀ = 1,0000, z ₀ = 1,0000,

y ₀ ^’ = (z ₀ – y ₀)· x ₀ = (1 – 1)·0 = 0; Δ y ₀ = h y ₀ ^’ = 0,1·0 = 0;

z ₀ ^’ = (z ₀ + y ₀)· x ₀ = (1 + 1)·0 = 0; Δ z ₀ = h z ₀ ^’ = 0,1·0 = 0;

- второй шаг: i = 1, х ₁ = х ₀ + h = 0 + 0,1 = 0,1;

y ₁ = y ₀ + Δ y ₀ ∙ = 1,0000 + ·0 = 1,0000;

z ₁ = z ₀ + Δ z ₀ ∙ = 1,0000 + 0 = 1,0000;

y ₁ ^’ = (z ₁ – y ₁)· x ₁ = (1 – 1)·0,1 = 0; Δ y ₁ = h y ₁ ^’ = 0,1·0 = 0;

z ₁ ^’ = (z ₁ + y ₁)· x ₁ = (1 + 1)·0,1 = 0,2; Δ z ₁ = h z ₁ ^’ = 0,1·0,2 = 0,02;

- третий шаг: i = 2, х ₂ = х ₁ + h = 0,1 + 0,1 = 0,2;

y ₂ = y ₁ + Δ y ₁ ∙ = 1,0000 + 0 = 1,0000;

z ₂ = z ₁ + Δ z ₁ ∙ = 1,0000 + 0,02 = 1,02;

y ₂ ^’ = (z ₂ – y ₂)· x ₂ = (1,02 – 1)·0,2 = 0,004; Δ y ₂ = h y ₂ ^’ = 0,1·0,004 = 0,0004;

z ₂ ^’ = (z ₂ + y ₂)· x ₂ = (1,02 + 1)·0,2 = 0,404; Δ z ₂ = h z ₂ ^’ = 0,1·0,404 = 0,0404.

Решение на остальных шагах приведено в табл.7.1

Таблица 7.1 – Решение системы ДУ

i	xi	yi +1 = yi -1+Δ yi- 1	yi^’ = (zi – yi)· xi	Δ yi = yi^’ · h	zi+ 1 = zi -1+Δ zi- 1	zi^’ = (zi + yi)· xi	Δ zi = zi^’ · h
	0,1	1,0000			1,0000
	0,2	1,0000			1,0000	0,2000	0,0200
	0,3	1,0000	0,004	0,0004	1,0200	0,4040	0,0404
	0,4	1,0004	0,018	0,0018	1,0604	0,6182	0,0618
	0,5	1,0022	0,048	0,0048	1,1222	0,8498	0,0850
	0,6	1,0070	0,1001	0,0100	1,2072	1,01071	0,1107
	0,7	1,0170			1,3179

Дата добавления: 2015-05-26