Пример 7.5

Проинтегрировать усовершенствованным методом Эйлера ДУ y’ = y – x при начальных условиях х ₀ = 0, у ₀ = 1,5 на отрезке [0, 1], приняв h = 0,25.

Первый шаг: i = 0, x ₀ = 0, y ₀ = 1,5.

y ^’₀₊₁ = y ₀ - x ₀ = 1,5 – 0 = 1,5; 0,1875;

x _0+1/2 = x ₀ + ; y _0+1/2 = y ₀ + ;

y’ _0+1/2 = y _0+1/2 – x _0+1/2 = 1,6875 – 0,125 = 1,5625; 0,3906;

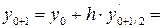1,5 + 0,3906 = 1,8906;

Второй шаг: i = 1, x ₁ = x ₀ + h = 0 + 0,25 = 0,25; y ₁ = 1,8906.

y ^’₂ = y ₁ – x ₁ = 1,8906 – 0,25 = 1,6406; 0,2051;

x _1+1/2 = x ₁ + ;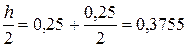

y _1+1/2 = y ₁ + ;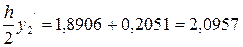

y’ _1+1/2 = y _1+1/2 – x _1+1/2 = 2,0957 – 0,375 = 1,7207; 0,4302;

1,8906 + 0,4302 = 2,3208.

За повышение точности приходится расплачиваться дополнительными затратами времени на вычисление функции .

Более высокая точность может быть получена, если улучшить аппроксимацию производной, сохраняя большее число членов ряда Тейлора.

7.3.4 Методы Рунге-Кутта

Метод Рунге-Кутта является одним из методов повышенной точности. Он имеет много общего с методом Эйлера. Метод Эйлера можно считать методом Рунге-Кутта первого порядка (в разложении в ряд Тейлора остается только первая производная).

Пусть требуется найти численное решение уравнения y ^’ = f (x, y) на отрезке [ a, b ] с начальными условиями у (х ₀) = у ₀.

Разобьем отрезок [ a, b ] на n равных частей с точками x_i = x ₀ + i·h (i = 0, 1,…, n), где h = (b - a)/ n – шаг интегрирования. В методе Рунге-Кутта, так же как и в методе Эйлера, последовательные значения y_i искомой функции у определяются по формуле

y_{i +1} = y_i + Δ y_i.

Если разложить функцию у в ряд Тейлора и ограничиться членами до h ⁴ включительно, то приращение функции Δ y можно представить в виде

, (7.2)

где производные находят последовательным дифференцированием из уравнения y ^’ = f (x, y).

Вместо непосредственных вычислений по формуле (7.2) в методе Рунге-Кутта определяют четыре числа:

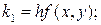
(7.3)

Можно доказать, что если числам k ₁, k ₂, k ₃, k ₄ придать соответственно вес 1/6; 1/3; 1/3; 1/6, то средневзвешенное этих чисел, т.е.

с точностью до четвертых степеней равно значению Δ у, вычисленному по формуле (7.2)

(7.4)

Таким образом, для каждой пары текущих значений x_i и y_i по формулам (7.3) определяют значения

(7.5)

по формуле (7.4) находят

Метод Рунге-Кутта имеет порядок точности h ⁴ на всем отрезке [ a, b ]. Оценка точности этого метода затруднительна. Грубую оценку погрешности можно получить с помощью «двойного просчета» по формуле

где у (х_i) – значение точного решения ДУ в точке х_i, а 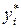и у_i – приближенные значения, полученные с шагом h /2 и h.

Если ε – заданная точность решения, то число n (число делений) для определения шага интегрирования h = (b - a)/ n выбирается таким образом, чтобы

h ⁴ < ε.

Однако шаг расчета можно менять при переходе от одной точки к другой. Для оценки правильности выбора шага h используется равенство

где q должно быть равно нескольким сотым, в противном случае шаг h уменьшают.

Дата добавления: 2015-05-26