Показатели силы связи для множественной регрессии

Существование корреляционной связи между факторами может быть выявлено с помощью показателей корреляции между ними, в частности, с помощью парных коэффициентов корреляции, которые рассчитываются по формулам:

.

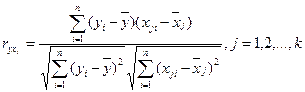Обычно кроме парных коэффициентов корреляции для отбора существенных факторов вычисляют частные коэффициенты корреляции, определяют надежность полученных коэффициентов регрессии по t- критерию и другие методы.

При анализе парных коэффициентов корреляции связи можно обратить внимание на то, что связи между изучаемыми переменными довольно сложным образом переплетаются между собой. Поэтому целесообразно рассмотреть вопрос о взаимосвязи между факторами при условии, что некоторые или все остальные факторы остаются неизменными.

Для выявления такой взаимосвязи используются коэффициенты частной корреляции. Эти коэффициенты позволяют элиминировать влияние на результат все факторных модельных признаков, кроме одного.

Расчет частных коэффициентов корреляции ведется через парные коэффициенты корреляции. С помощью частного коэффициента корреляции можно оценить свзяь между факторами у и х₁ при условии, что фактор х₂ закреплен на постоянном уровне (остается неизменным):

Если закреплен лишь один фактор, то такой коэффициент корреляции называется частным коэффициентом корреляции первого порядка. Если закреплены два фактора, то – второго порядка и т.д. Тогда обычный коэффициент парной корреляции можно называть частным коэффициентом корреляции нулевого порядка.

Частные коэффициенты корреляции второго порядка можно выразить через коэффициенты первого порядка при помощи соотношения

Аналогично можно записать соотношения, выражающий частный коэффициент корреляции k -го порядка через коэффициенты (k-1) -го порядка.

Дата добавления: 2015-05-26