Нахождение параметров линейных уравнений регрессии методом наименьших квадратов

Свойства коэффициента линейной корреляции.

1. r служит для определения тесноты линейной корреляционной зависимости;

2. r принимает значения от ;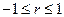

3. если r = 0, то между х и y не существует линейной корреляционной зависимости (но может быть не линейная);

4. чем ближе модуль r к 1, тем теснее линейная корреляционная связь;

5. если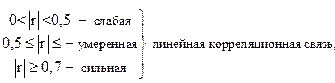

6. если 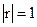, то между х и y возникает функциональная зависимость. Обе прямые регрессии совпадают;

7. значение r совпадает со знаком μ (см. ф-лу 11);

Если 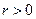, то между х и y существует прямая корреляционная зависимость, т.е. с ростом одной переменной другая, в среднем, тоже возрастает.

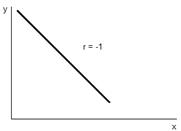
Если 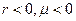, то между х и y существует обратная корреляционная зависимость, т.е. с ростом значений одной переменной, другая, в среднем, убывает.

После того, как сделана выборка, в линейных уравнениях регрессии I и II условные математические ожидания заменяются их оценками – групповыми средними. Тогда уравнения регрессии принимают следующий вид:

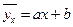- I

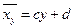- II

Метод наименьших квадратов состоит в том, что неизвестные параметры a и b – I, c, d – II находятся из принципа минимизации суммы квадратов расстояний от опытных точек, полученных по выборке, до теоретических точек, полученных соответственно по уравнениям I и II.

Для нахождения min указанной суммы, находятся частный производные и приравниваются к 0. Получается сумма уравнений, которые называются нормальными системами:

I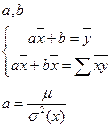

Коэффициент а в уравнении регрессии I называют коэффициентом регрессии y по x и обозначается:

(12)

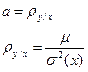
Тогда уравнение регрессии I приобретает вид:

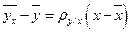- I

В дальнейшем для удобства 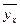обозначается y и уравнение I приобретает вид:

- I, где

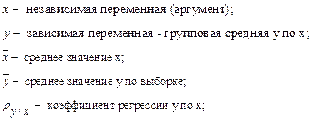
II аналогично с помощью M и K составляем систему нормальных уравнений для нахождения параметров c и d.

Коэффициент с обозначением называется коэффициентом регрессии x по y.

(13)

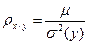
Тогда уравнение регрессии II приобретает вид:

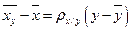- II

В дальнейшем для удобства 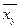обозначается y и уравнение II приобретает вид:

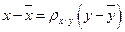- II, где

Дата добавления: 2015-05-26