Проверка значимости коэффициента корреляции

Связь между коэффициентами корреляции и коэффициентами регрессии.

Свойства коэффициентов регрессии.

1. коэффициенты регрессии имеют одинаковый знак, совпадающий со знаком μ;

2. коэффициенты регрессии являются угловыми коэффициентами для соответствующих прямых I и II относительно соответствующих осей, поэтому, если μ > 0 и коэффициент регрессии отрицателен, то обе прямые наклонены налево.

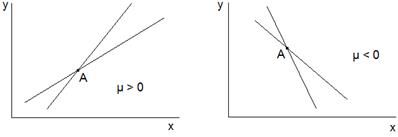
Замечание: Прямые регрессии пересекаются в точке А с координатами .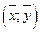

Сравнивая формулы 11, 12 и 13 получаем, что

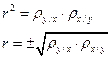, где значение r выбирается так, чтобы он совпадал со знаком μ.

Выдвигается гипотеза Н₀, которая заключается в том, что между переменными х и y во всей генеральной совокупности не существует линейной корреляции не существует линейной корреляционной зависимости.

Коэффициент линейной корреляции R равен 0, а его оценка r не равна 0 только потому что вместо всей генеральной совокупности рассматривается выборка. Фактически по выборке ни о чем не говорит. Значение r не равное 0 не значимо. Т.е. проверяется гипотеза Н₀: R = 0, линейной корреляционной связи нет. Для проверки этой гипотезы применяется t-критерий Стьюдента, статистика которого вычисляется по формуле:

(15)

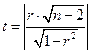
Эта статистика затабулирована в учебнике.

Критическое значение 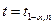определяется 2-мя параметрами:

1 – α, где α – уровень значимости;

n – объем выборки;

Опытное, или эмпирическое, значение t определяется по формуле 15. Если t больше t_{критич.} , то гипотеза Н₀ отвергается, т.е. значение значимо, между х и y существует линейная корреляционная зависимость.

Пример № 3:

10 участков земли обследуются с целью определения взаимосвязи между урожайностью Y и количеством внесенных удобрений Х. данные приведены в таблице. Предполагаем, что между переменными х и y существует корреляционная зависимость. Выполнить следующие задания:

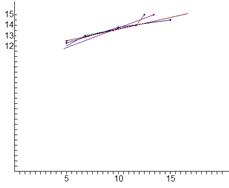
1) Вычислить групповые средние для х и для y и изобразить их на корреляционном поле, построив эмпирические линии регрессии;

2) Написать уравнения регрессии х по y и y по x и построить их графики на том же чертеже.

3) Вычислить коэффициент корреляции r и проверить его значимость при α = 0,05. сделать выводы о тесноте и направлении корреляционной связи.

4) Используя соответствующие уравнения регрессии вычислить среднюю урожайность когда количество удобрений равно 10 кг и сравнить с соответствующей средней.

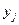
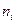
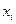
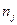
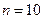
1)

а) групповые средние y по x:

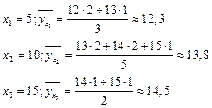
б) групповые средние x по y:

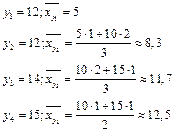
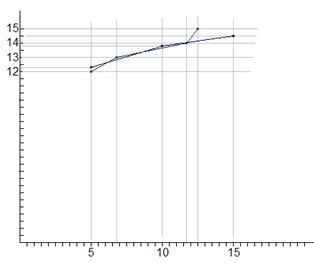
Предварительный анализ: по групповым средним построены эмпирические линии регрессии, точки которых образуют так называемое корреляционное поле. По результатам выборки можно предварительно заключить, что связь между переменными х и y прямая, т.е. с ростом значений одной переменной, групповые средние для другой переменной возрастают. Т.к. линии расположены близко друг к другу, можно предположить, что связь между х и y достаточно тесная.

2) для уравнений регрессии нужно вычислить:

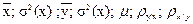
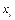
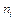
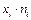
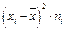
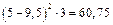
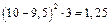
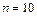
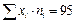
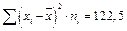
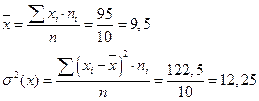
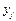
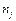
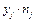
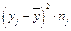
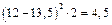
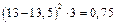
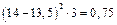
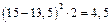
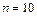
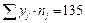
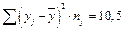
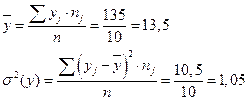
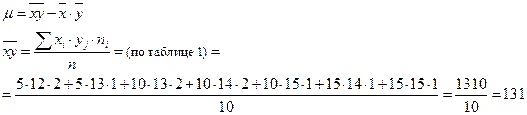
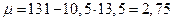
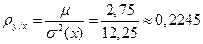
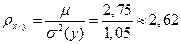
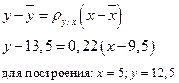
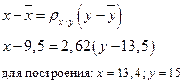
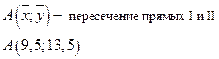
3) коэффициент линейной корреляции r можно вычислить по 2-м формулам:

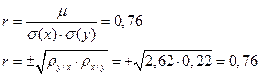
Вывод:

1) т.к. 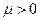, то между переменными х и y существует прямая зависимость, т.е. с ростом одной переменной, другая в среднем возрастает;

2) т.к. 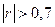, то связь между х и y – тесная;

3) т.к. коэффициенты регрессии > 0, то обе прямые наклонены направо;

4) т.к. связь тесная, то угол между прямыми маленький, прямые близко расположены друг к другу;

Проверка значимости коэффициента корреляции.

.

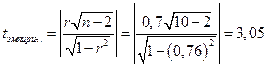
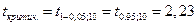Т.к. 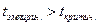, то коэффициент корреляции r значим, между урожайностью и количеством удобрений существует тесная корреляционная зависимость;

4) Дано: Х = 10 – аргумент.

Выберем то уравнение регрессии, в котором х является аргументом. Это уравнение I. Подставляем туда 10 и получаем.

Такой будет средняя урожайность при 10 кг удобрений.

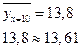значит модель адекватна действительности.

Замечания:

1. по уравнениям регрессии I и II можно делать прогнозы, однако эти прогнозы адекватны реальности (соответствуют действительности) только вблизи центра корреляционного поля (точки );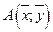

2. если предположить, что между х и y существует не линейная корреляционная зависимость, т.е. уравнения I и II не линейные, то их неизвестные параметры тоже можно найти методом наименьших квадратов.

Дата добавления: 2015-05-26