Свойства непрерывных функций. 1 страница

Група

Група

Група

ЗАВДАННЯ 7. Обчислити об’єм тіла, утвореного внаслідок обертання плоскої фігури, яка обмежена лініями.

Варіанти 1 – 15 – обертання навколо вісі О x; варіанти 16 – 30 – обертання навколо вісі О y.

1. y = x, x = 4, y = 0;

2. y ² = x, x = 1, y = 0;

3. x y = 4, x = 1, x = 2, y = 0;

4. y = 2x², y = 2, x = 0;

5. y = x ³, x = 2, y = 0;

6. y = e ^х, x = 0, x = 1, y = 0;

7. y = 4 x – x ², y = 0;

8. у = 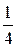x ², x = 4, y = 0;

9. y = , x = 1, x = – 1, y = 0;

10. y = x ², y = 0, x – 3 = 0;

11. y = 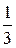(x ² + 3), x = 0, x = 3, y = 0;

12. y = ln x, x = e, y = 0;

13. y = x ², y = ;

14. y = x ³, y = 1, x = 0;

15. y = x ², y = х;

16. y = x ², 2 х – y = 0;

17. x y = 6, x = 0; y = 1, y = 6;

18. y = x ³, y = 1, x = 0;

19. x ² = – 2 y + 16, y = 0, y = 6;

20. y = , x = 1, x = 4, y = 0;

21. x ² = – 2 y + 4, y = 0;

22. x ² = – y + 4, y = 0;

23. y = ln x, y = 1, y = e;

24. y = x ² + 1, y = 3 х – 1;

25. y = ln x, y = 0, х = e;

26. y = x ², y = х;

27. y = e ^х, x = 0, x = 1, y = 0;

28. y = x ² + 1, y = 0, x = 1, x = 2;

29. y = 4 – x ², y = 0, x = 0, х ≥ 0;

30. y = e ^х, x = 0, y = e.

Таблиці вибору варіантів завдань для розрахунково-графічної роботи з розділу „Математичний аналіз функцій однієї змінної”

№ завдання № по списку

№ завдання № по списку

№ завдання № по списку

Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.

Теорема Вейерштрасса: Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Изображенная на рисунке функция 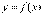непрерывна на отрезке и принимает свое наибольшее значение M в точке , а наименьшее m – в точке . Для любого 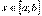имеет справедливо неравенство: .

Теорема о промежуточных значениях: Если функция непрерывна на отрезке 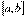и принимает на его концах неравные значения и , то на этом отрезке она принимает все промежуточные значения между A и B.

Геометрически теорема показана на рисунке.

Для любого числа С, заключенного между A и B, найдется точка с внутри этого отрезка такая, что . Прямая y=C пересечет график функции по крайней мере в одной точке.

16. Определение производной функции одной переменной. Геометрический, механический и экономический смысл производной.

Производной функции называется предел отношения приращения функции к приращению аргумента. Пусть функция y=f(x) определена в точке x и в некоторой ее окрестности. Дадим аргументу x приращение Dx, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции Dy и составим отношение. Если существует предел этого отношения при Dx®0, то указанный предел называют производной функции y=f(x) в точке x и обозначают f `(x).

Производная функции f в точке x0 есть скорость изменения функции в этой точке.. геометрическое толкование производной. Производная функции f в точке x0 определяется тангенсом угла наклона касательной, проведенной к графику функции f в точке х=x0. экономический смысл производной. Производительность труда есть производная от объема произведенной продукции по времени. Производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

17. Связь между свойствами непрерывности и дифференцируемости функции.

Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение не верно.

- непрерывна, но не является дифференцируемой в точке х=0 т.к. к ней нет касательной.

18. Производные элементарных функций. Основные правила дифференцирования. Производная второго порядка.

Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:

Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x² + (2x + 3) · e^x · sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	f(x) = C, C ∈ R
Степень с рациональным показателем	f(x) = x^n	n · x^n − 1
Синус	f(x) = sin x	cos x
Косинус	f(x) = cos x	− sin x (минус синус)
Тангенс	f(x) = tg x	1/cos^2 x
Котангенс	f(x) = ctg x	− 1/sin^2 x
Натуральный логарифм	f(x) = ln x	1/x
Произвольный логарифм	f(x) = loga x	1/(x · ln a)
Показательная функция	f(x) = e^x	e^x

Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.

1.

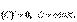
2. (справедлива для любого конечного числа слагаемых).

3. .

4. .

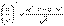а) .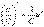

б) .

Когда мы дифференцируем функцию, каждой точке этой функции мы ставим в соответствие некоторое число – ее производную в данной точке. Таким образом, производная функции также является функцией.

Если функция дифференцируема, то ее производную называют второй производной от f и обозначают :

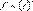
Вторая производная от параметрической функции x = x (t) и y = y (t) задается формулой:

19. Правило Лопиталя; раскрытие неопределенностей различных видов.

метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Если существует ,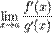

тогда существует .

20. Необходимый и достаточный признаки возрастания (убывания) функции.

Необходимые признаки: если дифференцируемая функция возрастает на некотором промежутке, то производная этой функции неотрицательна. Если дифференцируемая функция убывает на некотором промежутке, то производная этой функции не положительна.

Достаточный признак возрастания: Если производная дифференцируемой функции «+» внутри некоторого промежутка, то функция возрастает на этом промежутке. Если производная дифференцируемой функции «-» внутри некоторого промежутка, то функция убывает на этом промежутке.

21. Необходимое и достаточные условия экстремума функции.

Наличие max и min в отдельной точке промежутка Х не означает, что в этой точке функция приобретает наибольшее или наименьшее значение, т.е. глобальный max и min. Необходимые условия существования экстремума: Теорема Ферма: если точка х0 является точкой экстремума функции и в этой точке существует производная, то эта производная =0. Первое достаточное условие экстремума: если функция непрерывна, имеет производную в окрестностях точки х0 и при переходе через точку х0 меняет знак с «+» на «-», то х0 - точка max. Если при переходе черех точку производная меняет знак с «-» на «+», то х0 – min. Если производная при переходе через точку не меняет знак, то в этой точке нет экстремума.

22. Выпуклость и вогнутость графика функции. Достаточное условие выпуклости (вогнутости) графика функции.

Функция называется выпуклой вниз (вогнутой) на промежутке, если для любых 2-х точек Х1 и Х2 выполняется неравенство f(x1+x2)≤(f(x1)+f(x2))/2. Функция называется выпуклой вверз на промежутке, если для любых x1иx2 выполняется условие f(x1+x2)≥(f(x1)+f(x2))/2. График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Функция выпукла вниз (вверх)тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает.

23. Точки перегиба функции. Необходимое и достаточное условия перегиба графика функции. Асимптоты графика функции.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз, вверх. Необходимое условие перегиба: f’’(x) дважды дифференцируемая функция в точке перегибе х0 =0. Достаточное условие перегиба: если f’’(x) дважды дифференцируемая функция при переходе через некоторую точку меняет свой знак, то х0 - есть точка перегиба. Асимптомой графика функции называется прямая, обладающая тем свойством, что расстояние от точки (x; f(x)) до этой прямой стремится к 0 при неограниченном удалении. Асимптому нужно искать в точках разрыва или на концах ее области определения.

24. Определение дифференциала функции. Теорема о единственности дифференциала функции.

Дифференциал – величина, пропорциональная приращению независимой переменной и отличающаяся от приращения функции на бесконечно малую функцию высшего порядка. ∆y=f(x+∆x)-f(x) (приращение функции). Дифференциалом функции (обозначается через 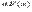) называется следующее выражение:

где dx -- дифференциал x при условии, что функция имеет производную.

Теорема о единстве дифференциала: Данная функция может иметь только 1 дифференциал.

25.Связь дифференциала функции с производной. Свойства дифференциала.

Если функция имеет дифференциал, то она имеет и производную. Следствие: если функция имеет производную, то она имеет и дифференциал. Дифференциал функции = произведению производной на приращение независимой переменной. dy= y’ ∆x. Дифференциал функции обладает свойствами, аналогичными свойствам производной.

1. Дифференциал постоянной равен нулю:
dc = 0, с = const.

2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const).

3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const).

4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой

26. Понятие производственной функции одной или нескольких переменных. Факторные модели производственно-экономических систем.

Производная функции – это функция, независимая переменная которой принимает значение использованного ресурса (фактора производства), ее независимая переменная – значение объемов выпускаемой продукции. Производная функции называется одноресурсной или однофакторной, ее область определения – множество неотрицательных чисел. Производные могут иметь разные области использования. Принцип – «затраты-выпуск» может быть реализован как микро-, так и на макро-экономическом уровне. производная может быть использована для описания отношений между годовыми затратами труда в масштабе региона или страны и годовым конечным выпуском продукции.

27. Средние, приростные и предельные показатели использования факторов производства в однофакторной модели.

Функция предложения заключается в общем виде в том, чтобы связать производство с потреблением, продажу товаров с их покупкой. Реагируя на возникающий спрос, производство начинает увеличивать выпуск товаров, улучшать их качество и уменьшать издержки, а тем самым увеличивать общий объем предложений на рынке. При изучении спроса различают реализованный (удовлетворенный), неудовлетворенный и формирующийся спрос. Функции полезности: одномерные и многомерные, аудитивные, порядковые и качественные, мультикативные, монотонные и немонотонные, линейные и нелинейные, одночисленные и поличисленные.

28. Приростная и предельная эластичности по его фактору

Дата добавления: 2015-05-26