Где Е – единичная матрица того же порядка, что и матрицы А и В

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Матрица, обратная к А, обозначается через А^-1, так что В= А^-1. Для матрицы А обратная ей матрица А^-1 определяется однозначно.

Справедливы следующие равенства:

1) D(А^-1)=(DА)^-1;

2) (А^-1)^-1=А;

3) (А₁А₂)^-1=А₂^-1А₁^-1;

4) (А^Т)^-1=(А^-1)^Т.

Существую несколько способов нахождения обратной матрицы. Рассмотрим один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем:

пусть нам дана матрица А, имеющая следующий вид:

Предположим, что DА¹0. Построим следующую матрицу С следующим образом:

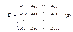
где А_ij – алгебраическое дополнение элемента а_ij в определителе матрицы А. Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать.

Полученная таким образом матрица С называется присоединённой к матрице А, или союзной с А.

Чтобы получить матрицу А^-1, обратную для матрицы А, необходимо каждый элемент присоединённой матрицы С поделить на DА, т.е. матрица А^-1 будет иметь следующий вид:

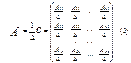
Пусть матрица А, имеет следующий вид:

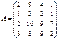
Чтобы найти матрицу А^-1, обратную для матрицы А, необходимо:

- вычислить определитель матрицы (DА= -3);

- найти алгебраические дополнения элементов а_ij в определителе матрицы А:

- составить присоединённую матрицу С по формуле (2);

- разделить все элементы матрицы С на DА.

65. Правило Крамера для решения системы п линейных уравнений с п неизвестными.

Составим определитель матрицы систе­мы А:

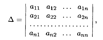
который называется также определителем системы. Заменим в этом определителе j- й столбец на столбец свободных членов В, т.е. получим этой заменой другой определитель, который обозначим Δ _j:

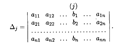
Пример 1. Найти решение системы уравнений

Решение. Составим и вычислим определители системы Δ и Δ _j (j = x, y, z):

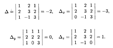
Определитель системы отличен от нуля, стало быть, она имеет единственное решение, которое вычисляется по форму­лам (15.6):

66. Декартова система координат. Прямая линия. Общее уравнение прямой линии на плоскости.

ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене).
Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни. Для задания декартовой прямоугольной системы координат выбирают взаимно перпендикулярные прямые, называемые осями. Точка пересечения осей O называется началом координат. На каждой оси задается положительное направление и выбирается единица масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A, B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:

67. Уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках; уравнение прямой, проходящей через две данные (несовпадающие) точки.

Дата добавления: 2015-05-26