Свойства непрерывных функций. 2 страница

ПРЕДЕЛЬНЫЕ И ПРИРОСТНЫЕ ВЕЛИЧИНЫ В ЭКОНОМИКЕ [differential values in economics] — предельная величина характеризует не состояние (как суммарная или средняя величины), а процесс, изменение. Поскольку в экономике большинство процессов, рассматриваемых как непрерывные (напр., рост производства или изменение его эффективности), являются функциями ряда аргументов (факторов), то предельные величины здесь обычно выступают как частные производные результативных показателей процесса по каждому из факторов.

Экономический смысл предельных величин состоит в том, что их можно использовать для принятия оптимальных решений с помощью методов дифференциального исчисления. Тогда, в частности, нахождение оптимума основывается на элементарных правилах: если при анализе функции первая производная равна нулю, это означает экстремум функции и, следовательно, возможный ее оптимум.

29. Показатели эффективности и эластичности для линейной и степенной производственной функции.

Способность спроса и предложения адаптироваться к изменившимся условиям рынка называется эластичностью (с точки зрения математики – эластичность – это отношение относительного прироста функции к относительному приросту независимой переменной). Зависимость объема спроса на товар от изменения цены на него называют эластичностью спроса по цене. Наиболее общее определение эластичности — отношение относительного приращения функции к относительному приросту независимой переменной.

Для рассматриваемых нами функций спроса и предложения такими независимыми переменными могут быть цены данного или других товаров, уровень доходов, издержек и т.д.

30. Функции полезности, спроса, предложения и их показатели эффективности и эластичности.

Наиболее общее определение эластичности — отношение относительного приращения функции к относительному приросту независимой переменной.

Для рассматриваемых нами функций спроса и предложения такими независимыми переменными могут быть цены данного или других товаров, уровень доходов, издержек и т.д.

Коэффициент эластичности показывает степень количественного изменения одного фактора (например, объема спроса или предложения) при изменении другого (цены, доходов или издержек) на1%.

Эластичность спроса или предложения вычисляется как отношение процентного изменения величины спроса (предложения) к процентному изменению какой-либо детерминанты.

Детерминанты — это факторы оказывающие воздействие на спрос или предложение.

31. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.

Пусть функция f(x) задана на некотором интервале R. Если найдется функция F(x), что при всех x€R, имеет место равенство F’(x)= f(x), то функция F(x)называется первообразной для функции f(x). Нахождение первообразной – это операция, обратная к операции вычисления производной. Неопределенный интеграл – множество первообразных функций. f(x) (ʃ f(x)dx). Свойства неопр интеграла: dʃ f(x)dx= f(x)dx, ʃF’(x)dx=F(x)+c.

32. Таблица простейших неопределенных интегралов. Основные методы интегрирования: замена переменной и интегрирование по частям.

Пользуясь тем, что интегрирование есть операция, обратная дифференцированию, нетрудно получить таблицу простейших интегралов.

Обращая формулы дифференцирования, получим:

Для вычисления неопределенного интеграла мы должны, если это возможно, привести его к табличным интегралам. Рассмотрим основные приемы интегрирования.

I. Метод разложения. Пусть . Тогда на основании свойства неопределенного интеграла имеем

,

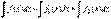причем слагаемые и стараются подобрать так, чтобы интегралы от них находились непосредственно.

II. Метод подстановки (метод введения новой переменной). Данный метод состоит в том, что в интеграле , нахождение которого затруднительно, вводят новую переменную t, связанную с переменной x соотношением

,

где – непрерывная строго монотонная функция, имеющая непрерывную производную 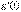на некотором интервале изменения , после чего получают

.

При этом стремятся подобрать такую подстановку , чтобы интеграл в правой части этого равенства был табличным или путь его нахождения был ясен. После того как этот интеграл найден возвращаются к первоначальной переменной с помощью обратной подстановки .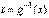

Заметим, что на практике часто встречаются интегралы вида

(57)

или интегралы, которые сводятся к такому виду. Подведем в этом интеграле множитель под знак дифференциала, а затем произведем подстановку . В результате получим формулу подстановки в неопределенном интеграле

,

которая упрощает подынтегральное выражение и во многих случаях способствует быстрому получению окончательного результата.

Частым случаем интеграла вида (57) является интеграл

.

Если – первообразная функции на некотором интервале 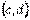, то, пользуясь подстановкой , получаем

. (58)

III. Метод интегрирования по частям. Пусть и – непрерывно дифференцируемые функции аргумента . На основании формулы дифференциала произведения имеем .

Отсюда

.

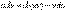Интегрируя обе части данного равенства, получим 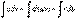или окончательно (так как )

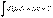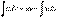. (59)

Эта формула называется формулой интегрирования по частям. Она показывает, что интеграл приводится к интегралу , который может оказаться более простым, чем исходный, или даже табличным.

К интегралам, которые находятся по формуле (59) относятся, например, интегралы вида

,

где 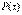– многочлен; 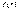– одна из следующих функций: . Чтобы свести в этом случае интеграл к табличному, надо последовательно применять формулу (59) столько раз, какова степень многочлена , причем в первый раз за выбрать и за выбрать .

33. Определенный интеграл. Формула Ньютона–Лейбница. Связь определенного и неопределенного интегралов.

Пусть функция f(x) непрерывна на отрезке [a,b], F(x) – ее первообразная при x€[a,b]. Под определенным интегралом ʃaͩ f(x)dx от данной непрерывной функции на данном отрезке [a,b] понимается соответствующее приращение ее первообразной F(b)-F(a). Формальная разница между определенным и неопределенным интегралом – определенный интеграл – это число, а неопределенный – это свойство функции. Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница = , здесь символ означает, что из значения при верхнем пределе b нужно вычесть значение при нижнем пределе a, — первообразная функция для .

34. Основные свойства определенного интеграла (общие свойства, свойства аддитивности, линейности, монотонности).

Общие свойства: величина определенного интеграла не зависит от обозначения переменной интегрирования ʃaͩ f(x)dx = ʃaͩ f(t)dt. Определенный интеграл с одинаковыми пределами интегрирования =0 ʃaͣ f(x)dx = F(a)-F(a)=0. при перестановке пределов интегрирования определенный интеграл меняет знак. ʃaͩ f(x)dx =- ʃdͣͩ f(x)dx.

Свойство аддитивности если промежуток интеграла разбит на конечное число промежутков, то определенный интеграл равен сумме опр. интегралов взятых по его частичным промежуткам.

Свойство линейности. Постоянный множитель можно выносить за знак определенного интеграла.. ʃaͩ Аf(x)dx=А. ʃaͩ f(x)dx, Определенный интеграл от алгебраической суммы равен той же алгебраической сумме определенных интегралов.. ʃaͩ f(x) +q(x) –h(x)dx= ʃaͩ f(x)dx+ ʃaͩ q(x)dx- ʃaͩ h(x)dx.

Свойство монотонности. Если подинтегральная функция определенного интеграла непрерывна и неотрицательна, а верхний предел > нижнего и не равен ему, то определенный интеграл тоже неотрицателен.

35. Приложения определенного интеграла: вычисление площадей плоских фигур, объёма тела вращения. Приложения определенного интеграла в экономических задачах.

С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.

Рассмотрим на плоскости Оху фигуру, ограниченную гра­фиком непрерывной и положительной функции f (x) на отрезке [ а, b ], отрезком [ а, b ] и вертикальными прямыми х = а и х = b (рис. 7.2). Эту фигуру будем называть криволинейной трапе­цией.

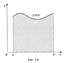
Величина площади криволинейной трапеции равна опреде­ленному интегралу от функции f(x) на отрезке [а, b]:

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х Î [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=πy^2.

Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,

у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен

36. Понятие функции нескольких переменных. График функции двух переменных. Линии уровня функции двух переменных.

Пусть каждой точке М из множества точек { М } по какому-либо закону ста­вится в соответствие некоторое число и из числового множес­тва U. Тогда будем говорить, что на множестве { М } задана функция и = f(M). При этом множества { М } и U называют­ся соответственно областью определения (задания) и областью изменения функции f(M).

Как известно, функция одной переменной у = f (x) изобра­жается на плоскости в виде линии. В случае двух переменных область определения { М_п } функции z = f(x, y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E³. Аналогичным образом функция от т пере­менных

Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (темпера­тура, давление и пр.).

Определение 2. Линией уровня функции двух переменных z = f(x, y) называется плоская кривая, получаемая при пе­ресечении графика этой функции плоскостью z = С, где С — постоянная величина, параллельной координатной плоскости Оху. Таким образом, можно сказать, что линии уровня функции z = f (x, у) — это семейство кривых на координатной плоскос­ти Оху, описываемое уравнениями вида

37. Полное и частные приращения функции нескольких переменных. Предел и непрерывность функции.

Пусть дана функция Z=f(x,y), совокупность значений x,y будем называть точкой. Дадим приращение ∆х переменной х, а y оставим без изменения. ∆f(x,y)=f(x+∆x,y)-f(x,y) –частное приращение функции по переменной х. ∆y f(x,y)=f(x,y+∆y)-f(x,y) – частное приращение по y.

∆f(x,y)=f(x+∆x,y+∆y)-f(x,y) – полное приращение.

Функция называется неприращенной в точке, если функция определена в данной точке и эта точка является предельной для области существования функции. И если бесконечно малым приращение переменных соответствует бесконечно малые приращения функции.

38. Частные производные первого и второго порядка функции нескольких переменных, их определения и правила вычисления.

Частные производные первого порядка

Пусть функция двух переменных z = f(x, у) определена в некоторой окрестности точки М (x, у) евклидова пространства Е ². Частная производная функции z = f(x, у) по аргументу x является обыкновенной производной функции одной перемен­ной х при фиксированном значении переменной у и обознача­ется как

Аналогичным образом определяется частная производная функции f (x, у) по переменной у в точке М, обозначаемая как

Функция, имеющая частные производные, называется диффе­ренцируемой.

Совершенно аналогично определяются частные производ­ные функций трех и более переменных. Частная производная функции нескольких переменных характеризует скорость ее изменения по данной координате при фиксированных значени­ях других координат.

39. Дифференциал функции нескольких переменных. Достаточное условие дифференцируемости функции.

Пусть функция z =ƒ (х; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М:

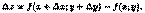
Функция z = ƒ (х; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде

где а = а(Δх, Δу)→0 и β=β(Δх,Δу)→0 при Δх→0, Δу→0. Сумма первых двух слагаемых в равенстве (44.1) представляет собой главную часть приращения функции.

Главная часть приращение функции z=ƒ(х;у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz:

dz=A*Δx+B*Δy. (44.2)

Выражения А•Δх и В•Δу называют частными дифференциалами. Для независимых переменных х и у полагают Δх=dx и Δу=dy. Поэтому равенство (44.2) можно переписать в виде

dz=Adx+Bdy. (44.3)

(достаточное условие дифференцируемости функции). Если функция z = ƒ(х;у) имеет непрерывные частные производные z'_x и z'_y в точке М(х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).

40. Необходимое условие существования полного дифференциала функции двух переменных

(необходимое условие дифференцируемости функции). Если функция z = ƒ(х;у) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные производные dz/dx и dz/dy, причем dz/dx = А, dz/dy = В.

41. Экстремум функции двух переменных. Необходимое и достаточные условия экстремума функции двух переменных.

Пусть функция z = f(x, y) определена на множестве { М }, а М ₀ (x ₀, у ₀) — некоторая точка этого множества.

Определение. Функция z = f(x, у) имеет в точке М ₀ локаль­ный максимум (минимум), если существует такая окрестность точки M ₀, принадлежащая { М }, что для любой точки М(х, у) из этой окрестности выполняется неравенство f(M) ≤ f(M ₀ ) (f (М) ≥ f (М ₀)); для случая функции трех и более переменных локальный экстремум определяется аналогично.

Согласно данному определению локального экстремума (минимума или максимума) полное приращение функции z = f(M) — f (М ₀) удовлетворяет одному из условий в окрест­ности точки M ₀:

Δ z ≤ 0, если M ₀ — точка локального максимума;

Δ z ≥ 0, если M ₀ — точка локального минимума.

. Если функция z = f(x, у) имеет в точке M₀ (x₀, y₀) локальный экстремум и частные производные пер­вого порядка, то все эти частные производные равны нулю:

Пусть в точке М₀(х₀, у₀) возможного экстре­мума функции и = f(x, у) и в некоторой ее окрестности все вторые частные производные этой функции непрерывны. Тогда если

то функция и = f(x, y) имеет в точке М₀ локальный экстре­мум: минимум при а₁₁ < 0 и максимум при а₁₁ > 0. Если же а₁₁а₂₂ — a₁₂² ≤ 0, то данная функция не имеет локального эк­стремума в точке M₀.

42. Глобальный экстремум функции; теорема Вейерштрасса.

43. Метод наименьших квадратов; построение эмпирических формул способом наименьших квадратов (линейная зависимость).

Пусть S зависит от t: S=f(t), причем функция, описывающая зависимость, точно неизвестна, известны только значения этой функции в отдельных точках, т.е. данные заданы в таблице. Задача состоит в том, чтобы вывести аналитическое отношение, которое описывает зависимость S=f(t).,такая зависимость называется трендом. Простейший подход к решению этой задачи состоит в том, что: заранее предполагается, что функция g, описывающая зависимость S=f(t), имеет какой то определенный вид, будем рассматривать функцию линейную, т.е. решим задачу об отыскивании линейного тренда. S≈g(t)=a+bt, где a b -неизвестные постоянные коэффициенты. A и b находятся исходя из следующего условия: сумма квадратов отклонений трендовых значений в точке t от соответствующих заданных значений переменной S должна быть минимальной. F(a,b)= ∑(a+bt-S)² >0

ϑф =2∑(a+bt-S)=0 ϑф =2∑(a+bt-S)=0

ϑа ϑb

44. Средние, приростные и предельные показатели использования факторов производства в двухфакторной модели.

Рассмотрим процесс производства, в котором ресурсы преобразуются в определенный результат производства. В потребляемых ресурсах выделим 2 основных фактора производства: труд и капитал. Предположим, что факторы производства и его результат обладают однородностью, делимостью и поддаются количественному изменению х – труд, у – капитал. Результат производства зависит от его факторов. Z – результат. Зависимость Z= Z(х,у) – называется производством. Показатели эффективности использования факторов производства: показатель эффективности использования затрат труда называют производительностью труда, показатель эффективности использования капитала – фондом отдачи. Средняя производительность труда – это средняя величина результата, приходящаяся на каждую единицу затрат труда: Pa(x,y)=Z(x,y)/x.

Средняя фондоотдача – это средняя величина результата, приходящаяся на каждую единицу основных производственных фондов. Fa(x,y)=Z(x,y)/y.

Приростная производительность труда – это средняя величина дополнительного результата, приходящаяся на каждую дополнительную единицу дополнительно использованных единиц затрат труда. Fa(x,y)= ∆Z(x,y)/∆x=Z(x+∆x,y)-Z(x,y)/∆x

Приростная фондоотдача – это средняя величина дополнительного результата, приходящаяся на каждую дополнительно использованную единицу основных производственных фондов:

Fa(x,y)= ∆Z(x,y)/∆у=Z(x,у+∆y)-Z(x,y)/∆у

Предельная производительность труда – это предел приростной производительности труда при условии, что дополнительная величина затрат труда стремится к 0.

P(x,y)=lim P∆(x,y)= lim(∆Z(x,y)-Z(x,y))/∆x

Предельная фондоотдача – это предел приростной фондоотдачи при условии, что величина дополнительно используемых основных производственных фондов стремится к 0.

f(x,y)=lim f∆(x,y)= lim(∆Z(x,y)-Z(x,y))/∆y/

45. Производственная функция Кобба-Дугласа. Экономический смысл ее параметров, показатели эффективности и предельной эластичности по каждому фактору.

Производственная функция Кобба-Дугласа - зависимость объема производства (Q) от создающих его труда (L) и капитала (K).

Общий вид функции:

Где А — технологический коэффициент, α — коэффициент эластичности по труду, а β — коэффициент эластичности по капиталу.

46. Понятие п-мерного вектора. Линейные операции над векторами. Свойства линейных операций.

. Любой упорядоченный набор из п действи­тельных чисел a ₁, a ₂,..., а_п называется п-мерным вектором ; при этом числа, составляющие упомянутый набор, называются координатами (компонентами) вектора .

Определение 2.Совокупность всех n -мерных векторов назы­вается n - мерным векторным пространством Rⁿ.

Координаты n -мерного вектора можно расположить либо в строку:

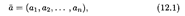
либо в столбец:

Определение 3. Два вектора с одним и тем же числом коор­динат

называются равными, если их соответствующие координаты равны, т.е.

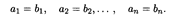
Определение 4. Вектор, все координаты которого равны ну­лю, называется нулевым вектором

Дата добавления: 2015-05-26