Ограничения ненаправленного эксперимента

Ограничения математического анализа

Лекция 2

Идеальная научная теория состоит из минимального количества аксиом (основных понятий и принципов), из которых решение любой задачи может быть получено формальной логикой, т.е. математически. К сожалению, сложность большинства явлений и пределы аналитических способностей человека (даже с электронными помощниками) ограничивают применение строгой теории лишь к сравнительно простым случаям.

Например, можно точно рассчитать сопротивление при движении жидкости в трубе в случае ламинарного течения, чего нельзя сказать о турбулентном течении. Т.е. сложные состояния потока могут быть подвергнуты теоретическому анализу лишь при игнорировании некоторых, не поддающихся учету сторонам движения. В ряде случаев результаты имеют достаточную для практики точность, в других – математические трудности настолько значительны, что без существенных упрощений решений получить не удается. Подобные трудности математического порядка уже давно заставили ученых идеализировать многие процессы. Так, например, в гидромеханике появилось понятие идеальной жидкости, а в теории упругости понятие идеального упругого тела. Для этих моделей разработаны строгие теории движения и деформации. Теоретические решения, полученные для таких идеализированных моделей сред, подчас сильно отличаются от наблюдаемых на практике. Отсюда следует, что при пользовании математическим аппаратом, любая задача должна быть упрощена, но обязательно опытным путем нужно установить предельные теоретические допущения, которые обосновываются физически, а не только удобны математически.

Вывод: математический анализ явлений должен быть ограничен реальными гипотезами и обязательно подвергнут экспериментальной проверке.

Если слепая вера в математический анализ явления приводит часто к ошибочным выводам, то возникает естественный вопрос: зачем тратить время на теорию, раз неизбежно требуется ее экспериментальное подтверждение? Таким вопросом часто задавались инженеры прошлого, накапливая натурные и лабораторные данные, но, не осмысливая их научно. До тех пор пока задачей является определение одной независимой величины (вес, время и т. п.), то достаточно бывает одного точного измерения; но если имеются две взаимосвязанные величины, то для установления функционального соотношения между ними, требуется уже несколько хорошо обдуманных измерений. Если же параметров больше, то количество измерений неизмеримо возрастает. Очень редко удается свести задачи к минимальному количеству входящих в них параметров без существенных упрощений.

Наглядной иллюстрацией потери времени на чистое экспериментирование является задача о нахождении сопротивления в трубах. Эта инженерная задача включает, по крайней мере, шесть измеренных: диаметр, шероховатость стенок, скорость, перепад давления, плотность и вязкость жидкости. Многие годы экспериментирования приводили к получению целого лабиринта не связанных между собой кривых, не помогали ни проверенные исследования, ни корреляция имеющихся данных.

И только с помощью теоретического руководства, учитывающего физику явления и размерностные стороны задачи, удалось поставить целенаправленные эксперименты.

Выводы: так же как и теория целиком зависит от направляющего экспериментального контроля, так и эксперимент, чтобы быть эффективным, никогда не может обойтись без аналитического руководства.

Соображения о размерности

1. Размерная однородность

Все физические величины измеряются путем сравнения с единицами той или иной размерной категории. Вывод этих категорий так и самих единиц измерения совершенно произволен. С целью упрощения задач рекомендуется уменьшение, если не самого числа единиц, то, по крайней мере, числа категорий. В механике все величины обычно выражаются в виде той или иной комбинации длины, времени, силы и (или) массы.

Так как каждая физическая величина имеет свойственные ей значения и размеры, то соотношения между двумя и большим количеством величины подразумевает эквивалентность их размерностей.

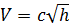
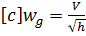
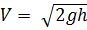- формула Торичелли

Иными словами обе стороны равенства должны быть равны не только в числовом выражении, но обладать одинаковыми размерностями. Так как любая размерность в механике зависит от трех основных категорий, то все механические соотношения можно свести к безразмерной форме.

2. П – теорема

Безразмерное произведение «n» размерных величин в общем случае может быть представлено в виде:

,

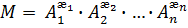здесь 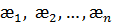– отвлеченные (безразмерные) числа такой величины, так чтобы степень каждой из «m» участвующих размерных категорий равнялась нулю.

Например, сопротивление в гладкой трубе зависит от пяти величин: D, V, ρ, μ, .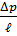

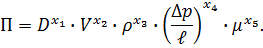
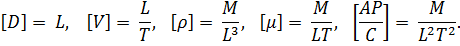
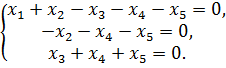
Три уравнения с 5 неизвестными имеют бесконечно много решений, т.е. имеется бесконечное множество.

Но в теории линейных уравнений известно, что только ограниченное число комбинаций линейно независимо. В данном случае их два решения

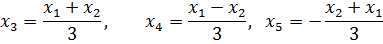
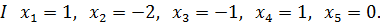
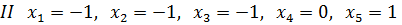
Получим:

	D	V	ρ		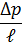μ
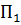
		-2	-1
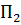
	-1	-1	-1

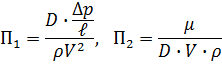
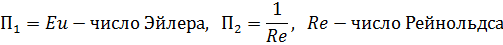
П – теорема гласит: если для описания какого-либо физического явления необходимо «n» величин и если эти величины влекут за собой «m» размерных категорий, то соотношение может быть сведено к такому, которое содержит n - r безразмерных произведений, причем 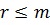является рангом 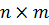размещений матрицы.

Таким образом 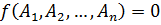по П–теореме

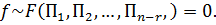
Каждая из безразмерных измеренных состоит из «r + 1» первоначальных единиц.

Возвращаясь к рассмотренному примеру о сопротивлении при движении жидкости в круглой трубе, отметим, что сопротивление

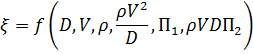
при различном выборе переменных, которым приписывают различные значения показателей степени, дают различные группы членов. П – теорема ясно показывает, что выбранные решения не независимы, и следовательно ни одно из них не может содержать ничего, чего не имелось бы в других соотношениях. Но вот вопрос о том, какую из различных форм предпочесть, остается открытым. Путем правильного выбора переменных, получающих произвольные показатели степени, можно управлять появлением величины в одном или большем числе произведений. Какие величины должны быть выбраны для появления в каждом произведении, а какие только в одном, зависит от ожидаемых результатов. Если переменную можно легко изменять в процессе эксперимента, то желательно ее присутствие, лишь в одном из безразмерных критериев, чтобы осуществлять его измерение.

Пример: число Рейнольдса 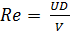. Переменная, выбранная в качестве зависимой величины, должна быть всегда ограничена одним безразмерным произведением (например, коэффициент сопротивления в трубе ξ). Но нужно всегда помнить, что безразмерные характеристические числа (произведения): Рейнольдса, Фруда, Маха и прочие, получившие большее физическое значение, будут получаться как произведения лишь в случае, если длина, скорость, плотность будут выбраны как повторяющиеся переменные. Как правило, не существует определенного пути для применения понятия размерности при анализе какого-либо явления, здесь необходим опыт.

Дата добавления: 2015-05-26