Экстраполяция

Метод ряда Тейлора.

Метод Лагранжа.

Этот метод очень важен потому, что им можно пользоваться для интерполяции даже в том случае, когда таблица содержит беспорядочную совокупность значений и , причем 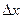непостоянно.

Интерполяционная формула Лагранжа

Количество членов в этом уравнении равно числу точек, использованных при интерполяции.

Применим в основном для таблиц, основанных на трансциндентных уравнениях.

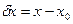
Есть еще метод Грегори-Ньютона, основанного на существовании зависимости

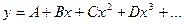
вводя 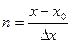, получают интерполяционную формулу

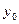- ближайшее меньшее значение к .

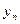Методы экстраполяции (т.е. получение значений вне таблицы данных) схожи с интерполяционными. Разница в точности результатов.

Если известна зависимость 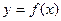, то любой метод хорош.

В других случаях лучше метод уравнений и Тейлора.

Несколько слов об округлении чисел и сохранениях, применяемых в таблицах.

Округления.

а) первая отображается цифра < 5;

б) первая отображается цифра < 5, но конец ≠ 0;

в) первая отображается цифра > 5, прибавляется единица.

Сокращения.

Если первая цифра не менее:

10,55

,58

,60

Значащие цифры.

(1) 123 см.

(2) 0,00123 км.

(3) 12,03 см.

(4) 12,30 см.

(5) 12300 см.

(1) Говорит о том, что указанная величина ближе к 123, чем к 122 или 124, т.к. 122,5 < < 123,5

(2) Тоже три значащие цифры, нули после запятой для указания разницы. (1) и (2) – идентичны.

(3) – четыре значащие цифры

(4) тоже четыре значащие цифры, но мы не знаем, что означает последний нуль.

В худшем случае 12,275 < < 12,325, если это правильно, то ближайшие большие значения, с точностью 0,05, могут быть 12,25 и 12,35.

Можно написать 12,3 вместо 12,30, но это не позволит судить о границах величин погрешности.

Выводы.

Таблицы, как одна из форм представления данных, содержит перечисление значений или свойств зависимого и независимого переменных, соответствующих друг другу в некотором определённом порядке. Таблицы характеризуются простотой, легкостью при использовании и компактностью, легкостью ввода в память ЭВМ.

Имеется три группы таблиц: таблицы качественных признаков, статистические и качественные, или таблицы функция. У статистической таблицы главными частями являются: название, аргумент, заголовки столбцы и значения или свойства табулируемых величин.

Таблица значений функций по форме сходна со статистической таблицей, но перечисляет значение зависимого переменного «» и независимого переменного «», соответствующие друг другу. Значения «» обычно (но не всегда) изменяются с постоянным шагом. Значения «» предпочтительно сглаживать, что можно сделать рядом способов:

1) беря соответствующие величины из уравнения, представляющего данные; 2) беря соответствующие величины с графика, на котором данные изображены в виде плавной кривой; 3) применяя поправки, получаемые с помощью какого-либо математического метода; 4) сглаживая разности элементов и используя их для получения приближенной сглаженной таблицы, сохраняющей общий ход несглаженных данных.

Последний способ является наилучшим при отсутствии уравнения, связывающего переменные.

Точность таблицы определяется числом значащих цифр ее элементов. Обычно последний знак элемента должен быть первым сомнительным знаком. Если ошибка не превышает 1,5 единиц, то допустим второй неточный знак 0 или 5, в зависимости от того, что ближе к истинному значению. Некоторые исследователи предпочитают не округлять последние знаки – округление производится по обычным правилам.

При пользовании таблицами часто приходится прибегать к интерполяции, для нахождения «», соответствующего некоторому промежуточному значению «». Интерполяция может быть выполнена графически, путем подбора плавной кривой на основании табулированных данных и нахождения значения «» по этой кривой.

Другие способы: а) метод линейной интерполяции (метод пропорциональных частей)

, где и 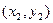- последовательные табличные точки, такие, что < < ;

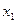б) Способ Грегори-Ньютона

, где 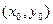- табличная точка к 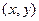, а ;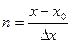

в) Метод уравнений состоит: в 1) выборе трех табличных точек , 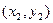и , ближайших к точке ;

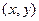2) в изменении системы координат по формулам

, ;

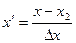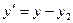3) в подстановке значени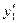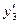й , и в уравнение

и разрешении этого уравнения относительно ;

4) в нахождении .

г) Метод Тейлора дает хорошие результаты для таблиц, основанных на известном уравнении.

д) Метод уравнения Лагранжа по формуле

Табличные значения можно экстраполировать применяя методы интерполяции к значениям «», экстраполяции в лучшем случае приближенные, а и то в случае, когда известен закон, связывающий «» и «». Экстраполяция для значений близких к границе, точнее чем для значений, далеких от границы.

Представление данных с помощью графиков.

Графический метод представления данных основан на применении принципов аналитической геометрии. При этом численные значения могут быть представлены в геометрической форме: длиной отрезка, площадью поверхности, объемом тела или величиной угла. Все измеримые величины могут быть представлены в таком виде, но это не означает, что все данные нужно наносить на график. Для одних данных – это потерянный труд, для других – это необходимость, позволяет легче заметить важные соотношения.

Преимущества графиков.

В пользу графиков можно сказать следующее:

а) облегчают сравнение величин;

б) фиксируют внимание исследователя;

в) позволяют легко найти нужные данные;

г) удобны для хранения.

Кроме этого позволяют легко обнаружить наличие максимумов и минимумов, точек перегиба, наибольшие и наименьшие скорости величин, периодичности или других важных свойств данных. Без графика некоторые важные свойства могут быть вовсе незамечены и выявляются потом в результате долгих скрупулезных рассмотрений табличных данных. Очень часто с помощью графика удается обнаружить существование функциональной зависимости между данными, кроме этого можно выполнять графическое дифференцирование и интегрирование не зная функциональной зависимости.

Графики можно разделить на две группы в зависимости от их назначения: иллюстративные и количественные.

Цель первых – дать качественную картинку некоторого процесса или некоторого состояния; целью вторых является быть количественным инструментом в различных исследованиях.

Иллюстрированные графики.

а)

а)

I II III IV V

б)

Дата добавления: 2015-05-26