Проверка пригодности эмпирической формулы для представления совокупности данных

Лекция 7

Выбор подходящего вида для эмпирической формулы.

Идеальная эмпирическая формула должна достаточно точно представлять экспериментальные данные и в то же время содержать как можно меньше произвольных постоянных. Эти два свойства, вообще говоря, противоположны друг другу. В следствии этого приходится жертвовать либо простотой формулы, либо точностью.

Часто приходится выбирать между несколькими формулами, примерно одинаково близкими к наилучшей. Существует несколько методов выбора наиболее подходящей формулы (с некоторыми я Вас познакомлю позднее). Обычно данные просто наносятся на график в виде точек, по этим точкам приближенно проводят кривую, а затем руководствуясь опытом и принципами аналитической геометрии, подбирают вид для этой кривой. Если при проверке этот вид уравнения окажется неудовлетворительным, то подбирают другой. Процесс продолжают до тех пор, пока не получится достаточно хорошее уравнение. Для повышения точности и облегчения этой процедуры нужно выбирать такую систему координат, в которой кривая, построенная по точкам, ближе всего к прямой. Правда тут возникает другой вопрос: каков будет «вес» отдельных экспериментальных точек на кривой при преобразовании координат. Существуют определенные правила подсчета весов, но об этом позднее.

К счастью, нет необходимости определять коэффициенты для каждого частного типа формулы, чтобы проверить, можно ли с помощью последней удовлетворительно представить совокупность данных. Существует ряд вспомогательных приемов, которые позволяют не только ответить на выше поставленный вопрос, но и оказываются весьма полезными при вычислении коэффициентов эмпирической формулы.

Для простых типов уравнений, содержащих одну или две произвольные константы, удобно пользоваться графическим методом проверки, для более сложных типов уравнений можно пользоваться табличными методами проверки.

Графический метод проверки.

Метод можно разбить на три этапа:

1) Предполагаемое соотношение 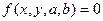следует записать в форме, линейной относительно двух выбранных функций и , не содержащих произвольных констант и

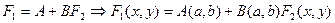
Часто одна из этих функций может зависеть только от 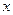, а другая от , а новые константы всегда только от и .

2) и следует вычислить для нескольких далеко отстоящих друг от друга пар .

3) Построить график, изображающий как функцию от .

Если при этом будет получена прямая линия, то это свидетельствует о том, что уравнение (исходное) удовлетворяет поставленным требованиям.

Пример:

,

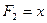
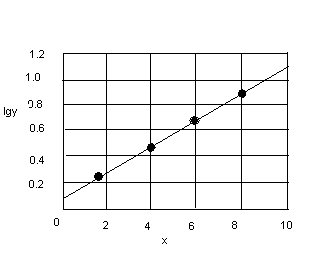
Такой метод применим для оценки пригодности уравнений типа:

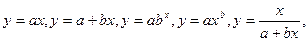и т.д.

Другие уравнения, содержащие две константы нельзя проверить указанным методом, так как они не поддаются записи в виде линейной функции.

Примеры: и т.д.

Табличный метод проверки.

Если уравнение содержит более двух произвольных констант, то для проверки пригодности предполагаемого вида формулы применяется табличный метод. Детали метода зависят от типа формулы, но в общих чертах он состоит из четырех этапов:

a. Нанесение экспериментальных данных в виде точек на график

b. Построение таблицы по этому графику

c. Вычисление последовательных разностей до некоторого порядка

d. Проверка приближенного постоянства старших разностей, что и является критерием пригодности предполагаемого вида формулы.

Если данные уже расположены в таблице, то два первых этапа исчезают.

Нетрудно вычислить порядок разностей, которые должны быть выполнены.

Пример 1: 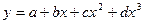(А)

Запишем

откуда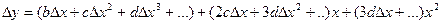

Т.к. должно оставаться константой в течении всего процесса проверки, то можно записать

,

Повторяя этот процесс, получим

, т.е. табличные разности третьего порядка будут оставаться постоянными. А это означает, что в пределах точности измерений формула (А) достаточно хорошо отражает связь между экспериментальными данными.

Сущность метода остается такой же и для других типов уравнений.

Пример 2. (В)

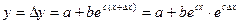
, где

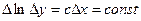
Такой критерий применим и к многим другим функциям, но не ко всем. Например, к таким как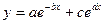

В таких случаях используют критерий более сложного вида.

Определение коэффициентов уравнения.

После того, как вид уравнения, назначенного для экспериментальных данных, выбран (или в случае полуэмпирического уравнения), задача сводится к определению коэффициентов уравнения. Для этой цели существуют различные численные методы, точность которых тоже весьма различна. Наиболее точным является метод наименьших квадратов (познакомимся подробно позднее), но он требует значительных затрат времени и более или менее сложных вычислений. Поэтому чаще применяются менее точные, но более простые методы. В последствии можно использовать метод последовательных приближений и уточнить коэффициенты.

Графический метод.

Можно сэкономить время, пользуясь вначале округлёнными, удобными для вычислений значениями коэффициентов, а затем уточнять их либо с помощью метода наименьших квадратов, либо последних приближений.

a) Две произвольные Const.

Применяется и дает хорошие результаты для уравнений с одной или двумя произвольными Const. Постоянные определяются графическим методом, который мы изложили выше при проверке пригодности формулы.

Продемонстрируем метод на простом примере:

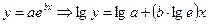
Если взять данные с графика 1, то

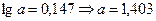
Уравнение:

Значения, вычисленные по этой формуле, хорошо согласуются с табличными данными.

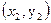В общем случае берут две точки на прямой и (подальше друг от друга). Тогда , .

Или записывается уравнение прямой с помощью определителя:

Раскладываем по элементам первой строки:

b) Три произвольные Const.

В этом случае мы должны прежде всего исключить одну из Const, а затем применить выше изложенный способ. Выбор схемы для исключения Const зависит от типа уравнения. Вот некоторые из них для наиболее часто встречающихся уравнений:

1)

2)

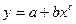
3)

Для уравнения 1):

Это парабола, пересекающая ось y в точке a. Если некоторые точки на графике близки к оси или если кривая может быть экстраполирована до оси , то a легко определяется. Затем вводят новую переменную и составляют уравнение 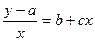и проводят анализ этого уравнения, содержащего 2 Сonst. Если не удается надежно экстраполировать кривую до оси у, то выбирают на графике какую-либо точку и переносят туда начало координат. В новой системе наблюденные точки будут иметь координаты 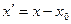, , а уравнение примет вид:

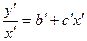или .

и 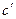находятся из графика , а величины a, b, c из соотношений:

, , .

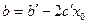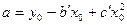Для уравнения 2):

Выбираем на экспериментальной кривой три далеко отстоящие точки , , 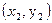так, чтобы выполнялось соотношение 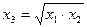. Тогда из 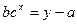следует 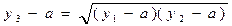, так как

.

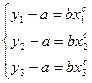
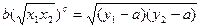Теперь найдем а по формуле .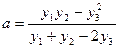

Определив а и вводя новую переменную , запишем исходное уравнение в виде , а это уже уравнение с двумя Const, которые можно определить, как было показано выше, графически по кривой 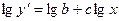. Если точность вычислений недостаточна, то используют повторные пробы.

Для уравнения 3):

Коэффициент а с кривой просто так найти нельзя. Делается это следующим образом: выбираем три точки на кривой (достаточно далеко друг от друга) такие, чтобы удовлетворить равенству .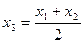

Тогда для всех точек, поэтому

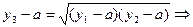
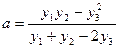
Далее, положив , приходим к уравнению с двумя Const: .

Рассмотрим еще два метода:

Метод избранных точек:

1. на график наносится значение y как функции х, проводится плавная кривая.

2. на кривой выбираются «n» точек (столько, сколько нужно определить коэффициентов). Для удобства значения х должны совпадать с делениями сетки и подальше от концов.

3. каждая из пар подставляется в уравнение, что дает n- уравнений.

4. система решается относительно коэффициентов

Замечание: уравнение не всегда линейное относительно коэффициентов, поэтому указать заранее методы ее решения невозможно.

Пример:

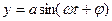- a и - неизвестные Const

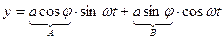- линейное соотношение

Найдя и 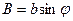, находим , .

Последовательные приближения:

Пусть

1. нашли коэффициенты каким-либо способом (первое приближение)

2. второе приближение

a) для различных х вычисляем

b) наносятся на график

3. находят уравнение кривой каким-либо способом

4. поправочное уравнение прибавляют к уравнению первого приближения получается уравнение второго приближения и так далее.

Выводы:

Если через точки, нанесённые на график, можно провести плавную кривую, то часто бывает целесообразно представить эти данные с помощью уравнения. Подбор эмпирического уравнения состоит из двух этапов:

1. нахождение подходящей формы уравнения для представления данных

2. нахождение соответствующих значений коэффициентов.

В случае полуэмпирического уравнения выполняется только второй этап. Общего правила для выбора подходящего вида эмпирической формулы не существует; можно лишь догадываться о подходящей форме уравнения по форме кривой. Однако существуют способы проверки удачного выбора той или иной догадки. Для уравнений, содержащих один или два параметра, можно применить графический метод проверки; для случая трех и более параметров – метод табличный, то есть критерий постоянства старших разностей.

Из методов для определения коэффициентов уравнения наиболее точным считается метод наименьших квадратов.

Из других методов отметим:

a) графический, применяемый для большинства уравнений с двумя и даже с большим числом коэффициентов. Метод достаточно точен.

b) Метод избранных точек, применимый почти для всех типов уравнений, но наиболее удобный для уравнений, приводимых к линейному уравнению относительно коэффициентов. В случае трех и более Const метод достаточно точен, особенно, если затем используются последовательные приближения.

c) Метод средних значений. Специальный вид метода избранных точек, применяемый к уравнениям – линейным относительно коэффициентов. Он не требует построения графиков.

Результаты могут улучшаться методом последовательных приближений.

Дата добавления: 2015-05-26